Обнинский Институт Атомной Энергетики

Кафедра Общей и Специальной Физики

Отчет по лабораторной работе №7

«Изучение плоскопараллельного движения на примере маятника Максвелла»

Выполнил: Пениос Марк Викторович

Студент группы ИС-Б21

Обнинск 2021

Цель работы: изучить плоскопараллельное движение и проверить справедливость уравнений, с помощью которых его можно описать.

Приборы: маятник Максвелла, штангенциркуль.

Таблица измерений t (с)

№	1	2	3	4	5	6	7	8	9	10	<t>
1	1,654	1,649	1,652	1,653	1,652	1,652	1,655	1,665	1,664	1,647	1.654
2	1,562	1,573	1,558	1,607	1,567	1,565	1,564	1,615	1,603	1,559	1.577

m_{1 кольца}=0.5125 кг m_{стержня}= 0,0333 кг

m_{2 кольца}=0.2573 кг m_диска=0,1225 кг

R₁=0.0525 м (внутр) R_{стержня}=0,005 м

R₁=0,043 м (внеш) R_диска=0,043 м

R₂=0.0525 м (внутр) S=0.27 м

R₂=0,043 м (внеш)

Для m₁: Для m₂:

S_n= =0.0059 S_n= =0.022

S₁= = =0.0019 S₂= = =0.007

Δt_сл= t_a,n*S t_a,n= 2.3(a = 0.95, n = 10 )

Δt=2.3*0.0059=0.014 Δt=0.022*2.3=0.05

Ϭ= = =0.008 Ϭ= = =0.014

Для нахождения момента инерции находим полную массу (масса съемного кольца + масса диска + масса валика)

<m>=<m_в>+<m_д>+<m_c>

<m₁>=0.5125+0,1225+0,0333 =0.67 кг

<m₂>=0.2573+0,1225+0,0333= 0.41кг

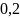m= = * кг

Вычислим момент инерции:

I_c = mr² т.к. величина >>1, то единицей можно пренебречь:

I_c = <m>r²

Для m₁:

I_c1=(0.5125+0,1225+0,0333)*0.005²( =0.00083 кг*м²

Для m₂:

I_c1=(0.2573+0,1225+0,0333)*0.005²( =0.00047 кг*м²

Вычислим относительную погрешность для I_c1

Для m₁ : Ϭ= = =0,017

Для m₂ : Ϭ= = =0,063

Абсолютная погрешность для m₁ :

ΔI = <I_c1>=0.017*0.00083=0.000014

Абсолютная погрешность для m₂ :

Δ I= <I_c1>=0.063*0.00047=0.00003

Момент инерции для m₁:

Момент инерции для m₂:

Упражнение №2.

Измерение диаметров валика, диска, сменного кольца и расчет момента инерции.

Полный момент инерции равен:

I_с2 =I_в + I_д +I_к

Находим средние значения моментов инерции валика, диска и сменных колец:

<I_в>= =4.16*10^-7

<I_д>=

<I_к>= ;

<I_к1>=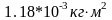 ; <I_к2>=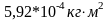

Находим относительную погрешность моментов инерции:

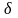_Iв=

_Iд =

I_д=<I_д>* _Iд= I_в=<I_в>* _Iв=

Находим абсолютную погрешность:

I_c1= =

I_c2= =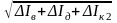

_Ic= I_c /<I_c> _Ic1=0,031 _Ic2=0,031

Полный расчетный момент инерции равен:

I_c1= I_в + I_д +I_к1=

I_c2= I_в + I_д +I_к2 =

Ответ:

I_c1=

I_c2=

Сопоставим значения I_c1 и I_c2

Ic1	Ic2
	Ic1=
	Ic2=

Вывод: : Экспериментально, с помощью маятника Максвелла изучил плоскопараллельное движение тела. Сопоставил значения моментов инерции маятника Максвелла.

Контрольные вопросы.

1. Такое движение твёрдого тела, при котором все точки описывают траектории лежащие в параллельных плоскостях.

2. Такое движение описывается двумя уравнениями динамики:

   • Уравнением динамики центра масс

(сумма внешних сил приложенных к телу)

• Уравнением моментов (для описания вращательной состовляющей плоского движения)

3. Ось проходящая через центр масс тела, которая может служить свободной осью.

4. Уравнение моментов относительно оси, проходящей через центр масс твёрдого тела (выбран центр масс). В этом случае сумма моментов сил равна 0. Уравнение моментов принимает в этом случае такой же вид, как и относительно оси, не имеющей ускорение.

6.