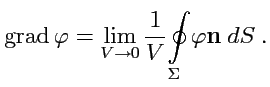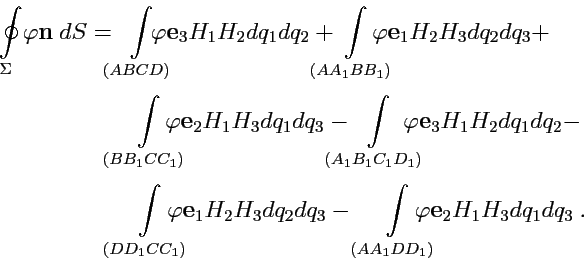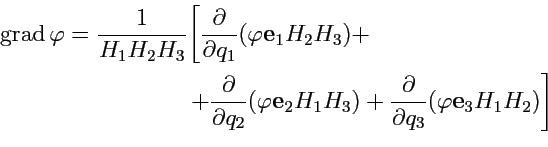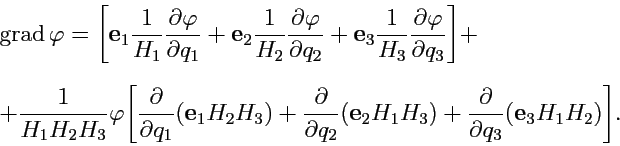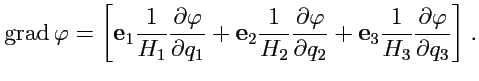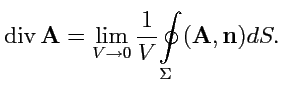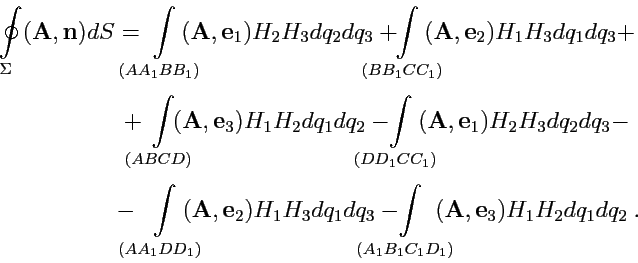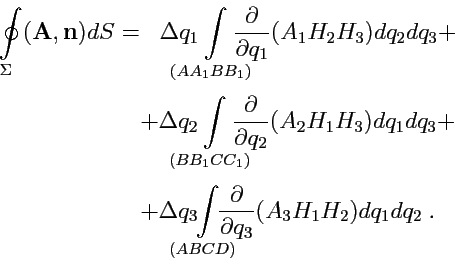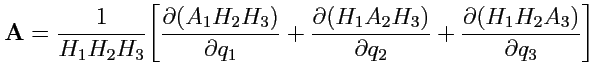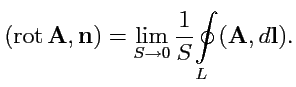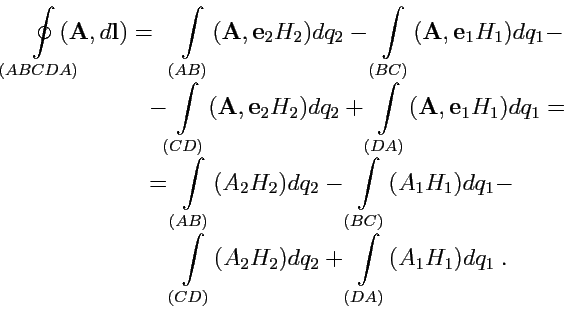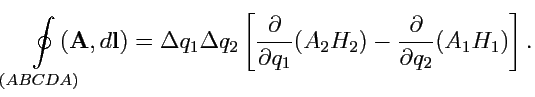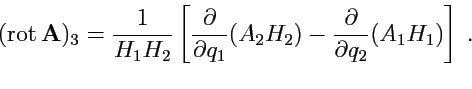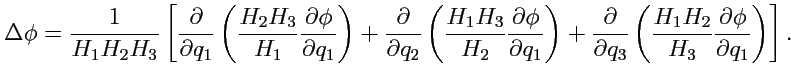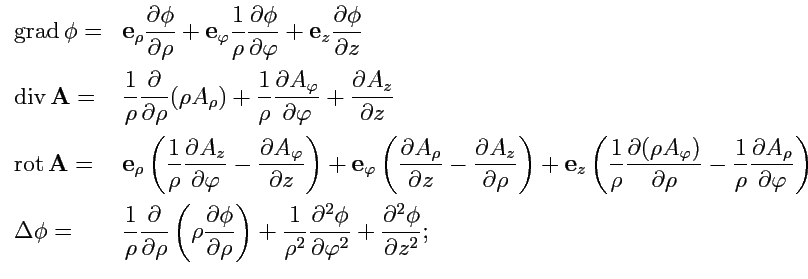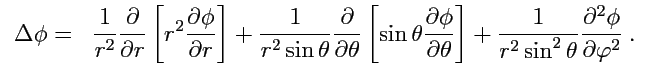- •Вопросы по ВиТа (Матанализу)
- •3. Несобственные интегралы, зависящие от параметра.
- •5. Эйлеровы интегралы: бета-функция и ее свойства (8 утверждений). Два вида записи бета-функции. Вычисление интеграла .
- •Доказательство.
- •8. Разбиение, диаметр разбиения, интегральная сумма. Определение и свойства кратных интегралов: интеграл Римана, свойства интегралов). Условия интегрируемости функции. Классы интегрируемых функций.
- •27. Криволинейная система координат. Коэффициенты Ламе. Выражение операций: градиент, дивергенция, ротор, оператор Лапласа в криволинейных координатах.
- •4. Оператор Лапласа определяется как . Тогда, используя выражения (230) и (234), получим:
27. Криволинейная система координат. Коэффициенты Ламе. Выражение операций: градиент, дивергенция, ротор, оператор Лапласа в криволинейных координатах.
Градиент скалярного поля. Пусть
дано скалярное поле ![]() .
Согласно ,
.
Согласно , ![]() определяется
как предел:
определяется
как предел:
|
Пусть также в области определения
поля
задана
криволинейная ортогональная система
координат. Рассмотрим в качестве
поверхности в (225)
бесконечно малый параллелепипед
объема ![]() (рис. 44)
(его гранями будут координатные
поверхности). Тогда, в силу малости этого
параллелепипеда, нормаль к каждой грани
будет совпадать с соответствующим
вектором репера:
(рис. 44)
(его гранями будут координатные
поверхности). Тогда, в силу малости этого
параллелепипеда, нормаль к каждой грани
будет совпадать с соответствующим
вектором репера: ![]() и
т. д. Учитывая, что, например, на
грани
и
т. д. Учитывая, что, например, на
грани ![]()
![]() и
аналогично на остальных, получим:
и
аналогично на остальных, получим:
|
Знак "минус" в последних трех слагемых появляется так как нормаль должна быть направлена во внешнюю область замкнутой поверхности.
Применяя теорему о среднем к (227), переходим к пределу в (225):
|
|
|
|
Так как ![]() ,
, ![]() ,
, ![]() и
и 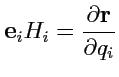 ,
то второе слагаемое в (229)
преобразуется к виду:
,
то второе слагаемое в (229)
преобразуется к виду:
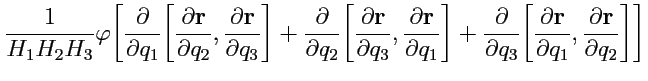
и обращается в ноль по свойству смешанных производных. Таким образом, формула для вычисления градиента скалярной функции в криволинейной ортогональной системе координат принимает вид:
|
2. Дивергенция
векторного поля. Получим выражение
для ![]() ,
используя общее определение дивергенции,
как предела:
,
используя общее определение дивергенции,
как предела:
|
Как и в первом случае, пусть объем ![]() ограничен
бесконечно малым параллелепипедом
(рис. 44).
Вычислим поток в (231):
ограничен
бесконечно малым параллелепипедом
(рис. 44).
Вычислим поток в (231):
|
Учитывая, что в ортогональной системе
координат ![]() ,
получим
,
получим
|
Применяя теорему о среднем и переходя к пределу (231), получим:
div |
3. Ротор
векторного поля. Согласно
определению (103),
проекция вектора ![]() на
произвольный вектор
на
произвольный вектор ![]() равна:
равна:
|
Если в качестве
выбрать
векторы репера ![]() ,
то величины
,
то величины ![]() будут
координатами вектора
в
системе координат, задаваемой тройкой
будут
координатами вектора
в
системе координат, задаваемой тройкой ![]() ,
т. е.
,
т. е. ![]() .
Найдем
.
Найдем ![]() .
Для этого вычислим циркуляцию поля
.
Для этого вычислим циркуляцию поля ![]() по
контуру
по
контуру ![]() (рис. 44).
Тогда
(рис. 44).
Тогда
|
Учитывая, что на линии ![]()
![]() ,
, ![]()
![]() ,
вместе с теоремой о среднем для каждого
участка контура, получим:
,
вместе с теоремой о среднем для каждого
участка контура, получим:
|
Аналогичные вычисления можно проделать
для векторов ![]() ,
, ![]() и
тогда из (235)
следует:
и
тогда из (235)
следует:
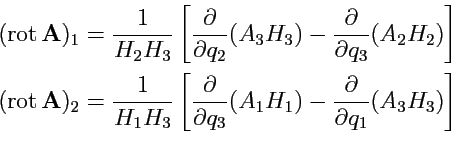
|
Так как ![]() ,
то (238)
можно переписать следующим образом:
,
то (238)
можно переписать следующим образом:
|
4. Оператор Лапласа определяется как . Тогда, используя выражения (230) и (234), получим:
|
С использованием общих выражений
для ![]() ,
,
и
,
,
и ![]() можно
получить следующие формулы для вычисления
в:
можно
получить следующие формулы для вычисления
в:
- цилиндрической системе координат ![]() :
:
|
- сферической системе координат ![]() :
:
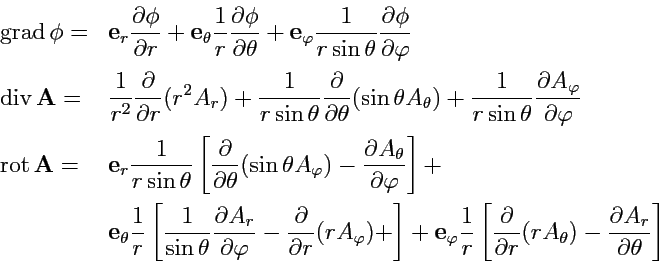
|
Пример
4-1. Вычислить ![]() ,
, ![]() и
и ![]() в
сферической системе координат.
в
сферической системе координат.
Решение. Радиус-вектор
в сферической системе координат имеет
вид ![]() ,
, ![]() и
тогда
и
тогда
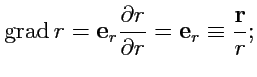
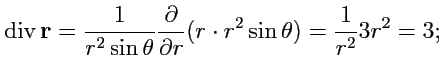
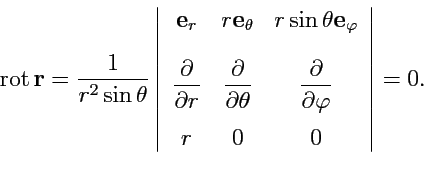
Пример
4-2. Вычислить ![]() ,
, ![]() Const.
Const.
Решение. Направим
ось ![]() вдоль
вектора
вдоль
вектора ![]() .
Тогда в сферической системе координат
.
Тогда в сферической системе координат
![]()
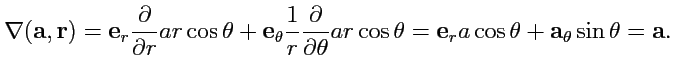
В цилиндрической системе координат
![]()
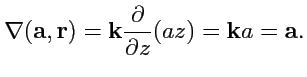
Как видно, цилиндрическая система координат в данном случае "выгоднее" сферической, что определяется свойством дифференцируемой функции, которая имеет цилиндрическую симметрию за счет выделенного направления, заданного вектором .
28. Выражение операций: градиент, дивергенция, ротор, оператор Лапласа в цилиндрической и сферической системах координат.
Вычисление градиента, дивергенции и ротора связано с однократным дифференцированием некоторых функций, поэтому эти операции называют дифференциальными операциями первого порядка.
![]()
Для скалярного поля был введен один оператор первого порядка
![]()
.
Для векторного поля введены два оператора первого порядка
![]()
.
Повторное применение оператора "набла" приводит к необходимости вычисления вторых производных. Т.о. мы приходим к дифференциальным операторам второго порядка.
Имеет смысл рассматривать пять дифференциальных операций второго порядка:
![]()
1) ;
![]()
2) ;
![]()
3) ;
![]()
4) ;
![]()
5) .
Будем считать, что необходимые условия дифференцируемости, непрерывности и пр. выполнены. Более детально эти вопросы обсуждаются в расширенных курсах высшей математики.
Оператор Лапласа
![]()
Рассмотрим скалярное поле . Существует единственный дифференциальный оператор, действующий на это поле
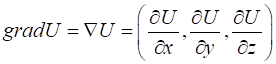
.
Полученный вектор указывает величину и направление максимального возрастания функции .
Вычислим в явном виде . Используя оператор "набла", имеем
![]()
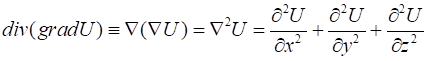
.
Убедимся в справедливости этого выражения путем непосредственного дифференцирования:
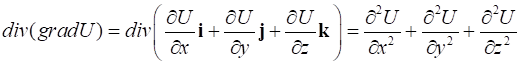
.
Выражение, естественно, получилось таким же.
Такое выражение часто встречается в различных задачах математической физики и для его записи введен специальный дифференциальный оператор второго порядка:
дифференциальная операция градиент дивергенция
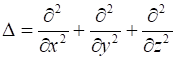
.
Этот оператор называют оператором Лапласа или лапласианом. Формально можно записать
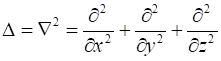
.
Итак, дивергенция градиента скалярной функции равна лапласиану этой функции. Оператор Лапласа широко применяется в различных задачах. Так, например, расчет температурного поля сводится к решению уравнения Лапласа
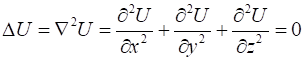
с соответствующими граничными условиями.
Градиент дивергенции
![]()
Рассмотрим операцию . В прямоугольной декартовой системе координат имеем
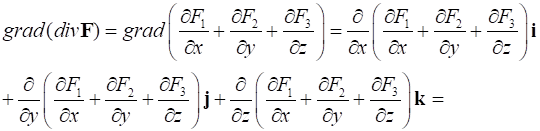
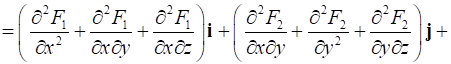
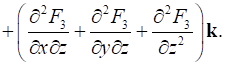
Полученное выражение является вектором, компонентами которого являются комбинации частных производных второго порядка.
Отметим, что некорректное использование оператора "набла" может привести к неверным результатам:
![]()
.
В этой формуле, которая отличается от полученной в начале параграфа, допущена ошибка в преобразовании
![]()
.
Три вектора, которые здесь используются, не образуют смешанное произведение векторов (в смешанном произведении ). Заменять действие двух операторов "набла" одним оператором Д недопустимо, т.к. их последовательные действия в отношении вектора F различаются.
Следует иметь в виду, что операции с оператором требуют внимания и аккуратности, поэтому соответствующие преобразования следует сопровождать непосредственными вычислениями, выполняя дифференцирование по координатам.
Дивергенция градиента и ротора
Дивергенцию градиента мы определили в §1
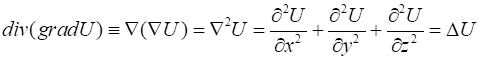
,
где был введен оператор Лапласа
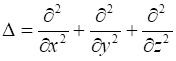
.
Найдем дивергенцию ротора с помощью оператора "набла":
![]()
.
Нетрудно убедиться в справедливости этого равенства и непосредственным дифференцированием. Предлагается сделать это самостоятельно.
В выражении рассматривается смешанное произведение трех векторов , и . Отметим отличие этого случая от выражения
![]()
,
![]()
которое не является смешанным произведением (выражение является скалярным произведением, а не векторным).