
- •Часть 2
- •Часть 2 Колебания и волны. Элементы квантовой и статистической физики.
- •1. Квантовая механика и физика атома
- •2. Элементы статистической физики и термодинамики.
- •1. Колебания.
- •2. Волны.
- •Вопросы для подготовки к экзамену По разделу «Элементы квантовой и статистической физики» Квантовая физика и физика атома.
- •Статистическая физика и термодинамика.
- •Основные физические постоянные (округленные значения)
- •Плотность твердых тел
- •Массы атомов легких изотопов
- •Масса и энергия покоя некоторых частиц
1. Колебания.
1.1. Общие представления.
Сформулируйте определение колебательного процесса. Какие различия по повторяемости и виду их колебательной функции можно выделить?
Как называются идеальные колебания и в чем заключается их совершенство?
В чем особенность периодических колебаний? Могут ли они представляться несинусоидальной зависимостью?
Обоснуйте роль инерции и наличие равновесного положения у системы в случае ее колебательного движения.
Какие колебания называют свободными, какие - вынужденными? В чем отличие последних от так называемых автоколебаний?
Могут ли свободные колебания быть затухающими? Какие реальные колебания являются незатухающими? Вспомните, при каком условии они возможны?
В чем состоят различия в путях восполнения энергетических затрат системы в случае вынужденных, параметрических и автоколебательных процессов?
Можно ли утверждать, что условие малости колебаний (малых отклонений от положения равновесия) - главный признак их линейности? Зависит ли период таких колебаний от амплитуды?
Являются ли линейными гармонические колебания и автоколебания?
Приведите связь периода T и частоты колебаний υ. Какова взаимосвязь этих параметров с циклической частотой ω?
Известно, что для периодической функции справедливо представление f(t+T)=f(T). Убедитесь, что функция cos(ωt+α) является периодической при α = const и с учетом того факта, что ω выражается через период T.
Что называют сложением колебаний? Являются ли «биения» при колебаниях примером указанного процесса?
Напишите уравнения для двух простейших взаимно–перпендикулярных колебаний.
Что понимается под термином «фигуры Лиссажу»? В каких случаях при сложении взаимно–перпендикулярных колебаний они возникают на экране осциллографа?
1.2. Свободные колебания.
Как известно, уравнение x(t)=Acos(ω0t+α0) описывает гармонические колебания величины х . Что здесь называют смещением и что – фазой колебаний?
Являются ли амплитуда А и начальная фаза α0 в уравнении п.15 величинами, независящими от времени? Может ли в принципе амплитуда свободных колебаний измениться с течением времени?
Может ли смещение х иметь одинаковые значения для двух разных фаз колебаний уравнения п.15 φ= (ω0t +α0)? Если да, то на какую минимальную величину должны отличаться фазы колебаний такой системы (осциллятора)?
Представьте направленный отрезок (вектор), который совершает с постоянной циклической частотой ω вращение относительно некоторой точки О в плоскости листа. Спроецируйте конец этого вектора на некоторую ось (назовем ее ОХ). Запишите функцию x(t). Сравните ее с законом гармонических колебаний груза на пружине. Что схожего в этих процессах. Может ли полученная векторная диаграмма моделировать линейные колебания груза на пружине?
Как известно, дифференциальное уравнение гармонических колебаний имеет вид
 ,
где ω0
– собственная циклическая частота
колебаний. Убедитесь подстановкой,
что уравнение п.15 x(t)=Acos(
,
где ω0
– собственная циклическая частота
колебаний. Убедитесь подстановкой,
что уравнение п.15 x(t)=Acos( является решением указанного
дифференциального уравнения.
является решением указанного
дифференциального уравнения.Является ли дифференциальное уравнение п.19 однородным, линейным? Каков его порядок? Одинаков ли порядок двух уравнений и
 +βх=0?
Если нет, то у какого из двух уравнений
он выше?
+βх=0?
Если нет, то у какого из двух уравнений
он выше?Какие колебания описывает дифференциальное уравнение
 +2β∙
+
+2β∙
+ =0?
Каков смысл входящих в него параметров
=0?
Каков смысл входящих в него параметров
 и β ?
и β ?Чему равна циклическая частота колебаний, описываемых дифференциальным уравнением п.21, в самом общем случае?
Отличаются ли собственные частоты свободных колебаний в случае затухающего и в случае незатухающего процессов?
Вспомните значения ω0 для трех простейших колебательных систем: математического маятника, идеального электрического контура, колеблющегося на пружине грузика?
Чему равно значение коэффициента затухания β в уравнении п.21 для колебаний грузика с массой m на пружине с жесткостью k при коэффициенте сопротивления среды r ?
Запишите выражение для β для случая затухающих колебаний электрического заряда в L–R–C контуре, считая известными значения индуктивности, емкости и активного сопротивления. Дайте выражение циклической частоты затухающих колебаний.
Как изменится частота гармонических колебаний математического маятника, если длина его нити увеличится в 4 раза? Как изменится период его колебаний?
Убедитесь, что период собственных затухающих колебаний груза на пружине при ω0 = 5,1π с -1 и β = π с -1 равен Т = 0,4 с.
Как изменится собственная частота колебаний груза на пружине, если ее жесткость уменьшится в 4 раза, а масса увеличится в 9 раз?
Уравнение гармонических (свободных, незатухающих) колебаний заряда в идеальном контуре Томсона имеет вид: q(t)=
 cos(
.
Используя выражение для силы тока в
контуре i(t) =
cos(
.
Используя выражение для силы тока в
контуре i(t) =  ,
убедитесь, что сдвиг по фазе между i(t)
и q(t) равен
,
убедитесь, что сдвиг по фазе между i(t)
и q(t) равен  (изменение тока опережает по фазе
изменение электрического заряда на
обкладках конденсатора).
(изменение тока опережает по фазе
изменение электрического заряда на
обкладках конденсатора).Убедитесь, что при гармонических колебаниях в электрическом L – С –R контуре в случае известных начальных значений
 = q( при t = 0) и для начальной фазы колебаний
= q( при t = 0) и для начальной фазы колебаний
 справедливо соотношение
справедливо соотношение
 .
.
Закон изменения напряжения на обкладках конденсатора в последовательном L–R–C контуре имеет вид
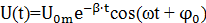 .
.
Что здесь является амплитудой колебаний напряжения?
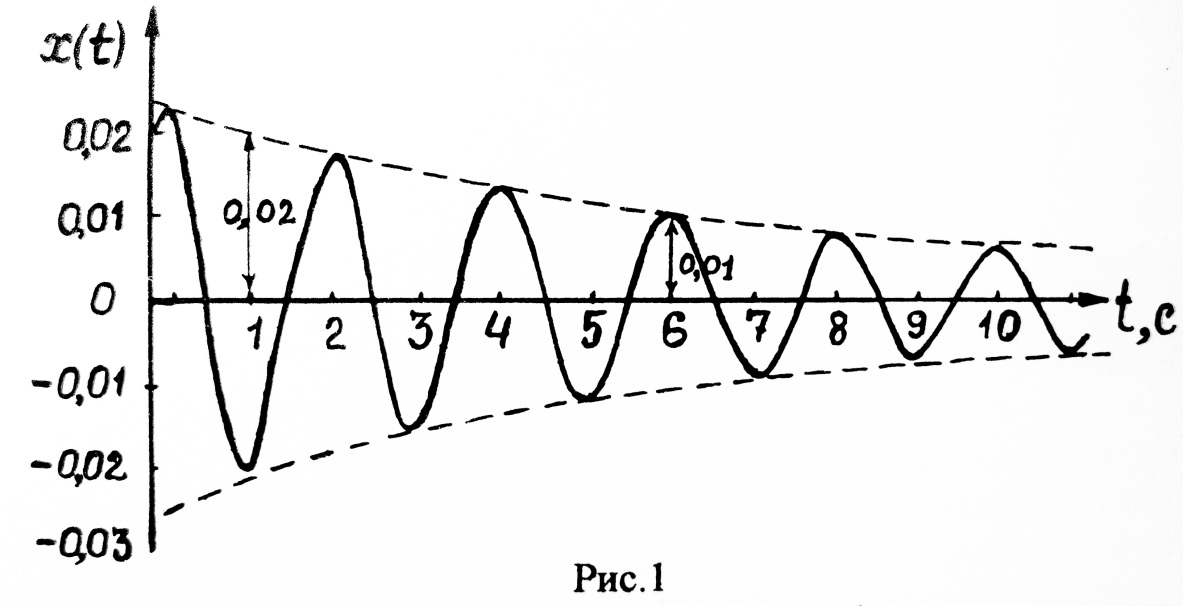
Функциональная зависимость изменения смещения x(t) для свободных затухающих колебаний представлена на рис.1. Штриховая огибающая удовлетворяет соотношению
 .
Найдите на рисунке значение начальной
амплитуды колебаний, определите период,
частоту и время релаксации колебаний.
Пользуясь данными рисунка, вычислите
значение коэффициента затухания β и
логарифмического декремента затухания
.
.
Найдите на рисунке значение начальной
амплитуды колебаний, определите период,
частоту и время релаксации колебаний.
Пользуясь данными рисунка, вычислите
значение коэффициента затухания β и
логарифмического декремента затухания
.
Как называют физическую величину, равную
 ? Если за время τ амплитуда убывает в
е = 2,7 раза, то следует ли из рис.1, что
? Если за время τ амплитуда убывает в
е = 2,7 раза, то следует ли из рис.1, что
 ?
?
Убедитесь, что значение β, приведенное в п.34, близко, к значению, полученному из выражения для логарифмического декремента затухания
 ,
где по определению
,
где по определению  .
Здесь N – число полных колебаний,
T – период, а под знаком логарифма
приведено отношение амплитуды колебаний
в разные моменты времени.
.
Здесь N – число полных колебаний,
T – период, а под знаком логарифма
приведено отношение амплитуды колебаний
в разные моменты времени.Дайте определение апериодического колебания и нарисуйте кривую
 ,
соответствующую такому процессу,
называемому иначе релаксационным.
,
соответствующую такому процессу,
называемому иначе релаксационным.Емкость электрического контура, в котором проходят свободные затухающие колебания
 Ф, индуктивность
Ф, индуктивность  Гн. Докажите, что критическое сопротивление
для контура
Гн. Докажите, что критическое сопротивление
для контура  Ом.
Ом.Убедитесь, что величина добротности
 для L–R–C контура, в котором проходят
затухающие колебания, безразмерна.
для L–R–C контура, в котором проходят
затухающие колебания, безразмерна.Покажите, что при апериодическом процессе (
 активное сопротивление электрического
контура равно критическому
активное сопротивление электрического
контура равно критическому  .
.
1.3. Вынужденные колебания.
Дифференциальное уравнение вынужденных колебаний некоторой системы имеет вид
 .
Запишите решение этого уравнения для
установившегося режима колебаний.
Объясните смысл входящих в него
параметров.
.
Запишите решение этого уравнения для
установившегося режима колебаний.
Объясните смысл входящих в него
параметров.С какой частотой в установившемся режиме происходят вынужденные колебания? Больше или меньше она , или всегда равна ей?
Может ли циклическая частота вынужденных колебаний в
 контуре, содержащем периодическую
э.д.с, меняющуюся с частотой
контуре, содержащем периодическую
э.д.с, меняющуюся с частотой  ,
быть больше или меньше резонансной
частоты
,
быть больше или меньше резонансной
частоты  ?
?Чему равна резонансная частота для силы тока в контуре п. 42?
Вынужденные колебания описываются уравнением
 .
Для какого режима колебаний это
возможно? Каков смысл параметра
.
Для какого режима колебаний это
возможно? Каков смысл параметра  ?
Имеется ли сходство таких (п.43) колебаний
с гармоническими?
?
Имеется ли сходство таких (п.43) колебаний
с гармоническими?Выражение
 определяет амплитуду вынужденных
колебаний некоторой колебательной
системы. Здесь
определяет амплитуду вынужденных
колебаний некоторой колебательной
системы. Здесь  амплитуда вынуждающей периодической
силы, т - масса колеблющегося элемента,
β - коэффициент сил сопротивления,
амплитуда вынуждающей периодической
силы, т - масса колеблющегося элемента,
β - коэффициент сил сопротивления,  собственная частота системы,
собственная частота системы,  частота вынуждающей силы – частота
колебаний. При каком значении
частота вынуждающей силы – частота
колебаний. При каком значении  амплитуда
колебаний
амплитуда
колебаний  будет
наибольшей?
будет
наибольшей?Можно ли утверждать, что решением дифференциального уравнения п.40 при
 является уравнение п.44.
является уравнение п.44.Сдвиг по фазе между вынуждающей силой
 и смещением
при вынужденных колебаниях дается
выражением
и смещением
при вынужденных колебаниях дается
выражением
![]() .
.
Покажите,
что для последовательного электрического
контура, для которого смещение ![]() ,
,
![]() для фазового сдвига справедливо
равенство
для фазового сдвига справедливо
равенство
![]() .
.
Покажите, исходя из выражения п. 45, что резонансная (при

амплитуда вынужденных колебаний имеет вид

Как
изменится эта формула, если затуханием
в системе пренебречь, т.е. считать ![]() ?
?
На рис.2 приведена в условных единицах резонансная кривая колебаний заряда в электрическом контуре. Исходя из смысла резонансной
 и
и 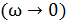 амплитуд, убедитесь, что добротность
электрического контура численно равна
3.
амплитуд, убедитесь, что добротность
электрического контура численно равна
3.На риз.3 приведены две качественные резонансные кривые
 для напряжения на конденсаторе – (1) и
силы тока
для напряжения на конденсаторе – (1) и
силы тока  – (2) в
контуре, содержащем периодическую
э.д.с. Пронумеруйте эти кривые. Запишите
выражения резонансных частот для обоих
случаев.
– (2) в
контуре, содержащем периодическую
э.д.с. Пронумеруйте эти кривые. Запишите
выражения резонансных частот для обоих
случаев.

Что определяет отношение
 для кривой рис.3 (см. пункт 49)?
для кривой рис.3 (см. пункт 49)?Что даёт сечение резонансной кривой
 по уровню
по уровню  ?
Что определяет отношение
?
Что определяет отношение  ,
где
,
где  и
и  – циклические частоты, отвечающие
указанному сечению?
– циклические частоты, отвечающие
указанному сечению?
