
Расчёт развёрток врезок конуса в цилиндр, шар, конус, тор
.doc31.03.2023г. Расчёт развёрток наклонного конуса (вариант II), врезок конуса в цилиндр, шар, конус, тор.
Дополнение к Формулам линий развёрток врезки штуцера в цилиндр, шар, конус, тор.
I. Конус-плоскость. Расчёт наклонного конуса. Rк=40мм; p=15; β=58,7. Вариант II.

В косоугольном треугольнике
![]() по теореме синусов
по теореме синусов
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() -
полярный радиус – переменная образующая
конуса, являющаяся гипотенузой
прямоугольного треугольника с катетами
-
полярный радиус – переменная образующая
конуса, являющаяся гипотенузой
прямоугольного треугольника с катетами![]() ;
;
![]()
![]() ;
;
![]() ;
;![]() ;полярный
угол
;полярный
угол
![]()
в полярных координатах
![]() в декартовых координатах:
в декартовых координатах:
![]()
В косоугольном треугольнике
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
уравнение эллипса в параметрическом
виде:
;
уравнение эллипса в параметрическом
виде:
![]()
![]() -
0 - 360
-
0 - 360
Для нанесения проекций вид В введём
дополнительные параметры:
![]() ;
;
![]()


-1-
II. Конус-цилиндр. Rк=36мм;
ρ=9,8;
Rц=40мм; β=54,5;
z₀Д=-15мм;
![]() ;
;

![]() ;
В косоугольном треугольнике
по теореме синусов
;
В косоугольном треугольнике
по теореме синусов
![]() ;
;
;
;
;
;
;
;
;
;
![]() - большая ось эллипса -
- большая ось эллипса -
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
По заданным и рассчитанным данным чертим
вид Д эллипс (сечение по НдОк),
![]() ;
;
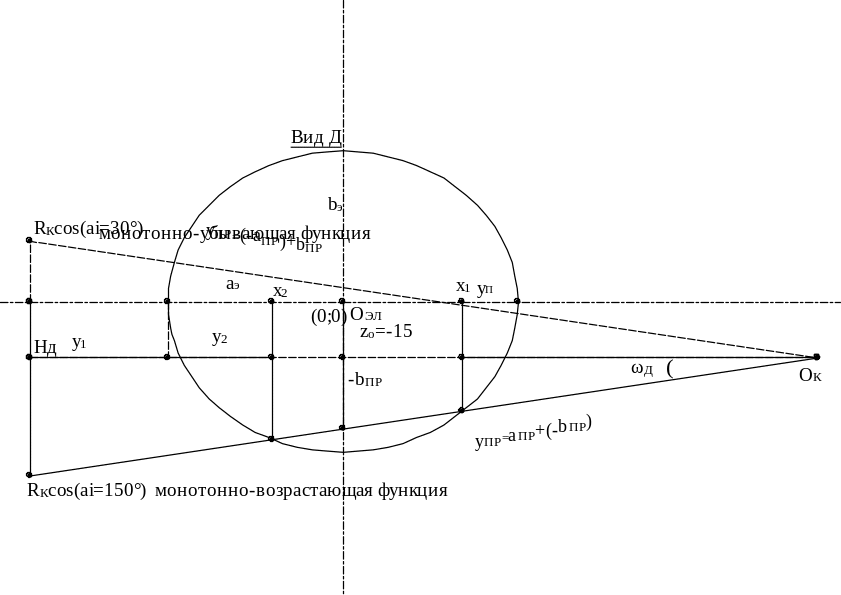
![]() ;
чтобы найти
;
чтобы найти
![]() нужно решить систему уравнений прямой
(Rкcosαi)Ок;
нужно решить систему уравнений прямой
(Rкcosαi)Ок;
![]() ;
и эллипса
;
и эллипса
![]() относительно
х.
относительно
х.
-2-
![]() ;
;
 ;
уравнение второй степени, приведём его
к виду:
;
уравнение второй степени, приведём его
к виду:![]() ;
корнями этого уравнения будут величины
;
корнями этого уравнения будут величины
![]() в точках пересечения прямой и эллипса.
в точках пересечения прямой и эллипса.
![]() ;
;

 ;
;
![]() ;
;
![]() ;
задача: выразить все коэффиценты через
;
задача: выразить все коэффиценты через
![]()
Важно!
![]() ;
(-)прямая является монотонно-убывающей
функцией, (+)монотонно-возрастающая. Вид
Д
;
(-)прямая является монотонно-убывающей
функцией, (+)монотонно-возрастающая. Вид
Д
![]() ;
по расположению на оси Y
при Х=0 (0;0)-центр эллипса (окружности;
параболы, гиперболы). Вид Д.
;
по расположению на оси Y
при Х=0 (0;0)-центр эллипса (окружности;
параболы, гиперболы). Вид Д.
![]() - смещение осей прибавляется к
;
соответственно расположению на оси Y
при Х=0 (0;0)-центр эллипса (окружности;
параболы, гиперболы). Вид Д.
- смещение осей прибавляется к
;
соответственно расположению на оси Y
при Х=0 (0;0)-центр эллипса (окружности;
параболы, гиперболы). Вид Д.
;
при
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;![]() -полуоси
эллипса (см. выше).
-полуоси
эллипса (см. выше).
-
полярный радиус «для раструба» –
переменная образующая конуса, являющаяся
гипотенузой прямоугольного треугольника
с катетами
;
;
![]() ;
;
;
полярный угол
;
полярные:
декартовы:
![]()
-
полярный радиус «для прокола» –
переменная образующая конуса, являющаяся
гипотенузой прямоугольного треугольника
с катетами
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
полярный угол
;
полярный угол
![]() ;
;
Для нанесения проекций на вид А введём дополнительные параметры:
для «раструба»:![]() ;
;
![]() ;
;
для «прокола»:
![]() ;
;
![]() ;
при этом следует учесть положение
проекций относительно центра системы
координат вида А и ввести соответствующие
поправки на смещение, поворот. Для
нанесения проекции на вид В найдём:
;
;
при этом следует учесть положение
проекций относительно центра системы
координат вида А и ввести соответствующие
поправки на смещение, поворот. Для
нанесения проекции на вид В найдём:
;
![]() ;
;
![]()


-3-
III. Конус-шар. Rк=40мм;
Rш=75мм; р=8˚ z₀=43мм;
![]() ;
;



;
![]() ;
;
;
;
![]() - находим, решая систему квадратных
уравнений прямой НдОк
- находим, решая систему квадратных
уравнений прямой НдОк
![]() и круга
и круга
![]() ;
;
![]() ;
для вида А
;
для вида А
уравнение второй степени, приведём его
к виду:
![]() ;
;
-4-
![]() ;корнями
этого уравнения будут величины
в точках пересечения прямой НдОк и круга
радиусом Rш.
;
;корнями
этого уравнения будут величины
в точках пересечения прямой НдОк и круга
радиусом Rш.
;
![]() ;
;
![]() - отрицательный, т.к. прямая НдОк –
является монотонно-убывающей функцией.
- отрицательный, т.к. прямая НдОк –
является монотонно-убывающей функцией.
![]() .
подставляем, находим
.
подставляем, находим
![]() ;
по заданным и рассчитанным параметрам
чертим вид Д (по сечению НдОк).
;
по заданным и рассчитанным параметрам
чертим вид Д (по сечению НдОк).
![]() ;
;
![]() находим, решая систему квадратных
уравнений прямой RcosаiОк
находим, решая систему квадратных
уравнений прямой RcosаiОк
![]() и круга
и круга
![]() ;
;
![]() ;
для вида Д
;
для вида Д
уравнение второй степени, приведём его
к виду:
![]() ;
;
![]() ;корнями
этого уравнения будут величины
в точках пересечения прямой RcosаiОк
и круга радиусом Rд.
;
;корнями
этого уравнения будут величины
в точках пересечения прямой RcosаiОк
и круга радиусом Rд.
;
![]() ;
;
![]() - кофф. положительный, т.к. прямая RcosаiОк
– является монотонно-возрастающей
функцией.
- кофф. положительный, т.к. прямая RcosаiОк
– является монотонно-возрастающей
функцией.
![]() ;
после подстановок находим полярный
радиус
;
после подстановок находим полярный
радиус
![]() ;
полярный угол
;
в декартовых:
;
полярный угол
;
в декартовых:

-5-
IV. Конус-конус. Задано:
конус1-врезка;
![]() ;
;
![]() ;
смещение осей
;
смещение осей
![]()
конус2-объект врезки;
![]() ;
;
![]() ;
;
![]() ;
;
В общем случае расчёт развёртки ведётся по трём совместным уравнениям прямой и кривым сечения конуса.
Для определения интервалов задаваемого
параметра, в которых находятся
соответствующие сечения, введём столбец
в Excel
![]() ;
эксцентриситет е<1
сечение – эллипс; е=1 – парабола; е>1
– гипербола.
;
эксцентриситет е<1
сечение – эллипс; е=1 – парабола; е>1
– гипербола.

-6-

Интервалы I, V;сечение
- эллипс
![]() центральный угол конуса-врезки.
центральный угол конуса-врезки.

в косоугольном треугольнике
![]() по
теореме синусов:
по
теореме синусов:![]() ;
;
-7-
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В треугольнике
![]()
![]() -большая
ось эллипса: по теореме синусов;
-большая
ось эллипса: по теореме синусов;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
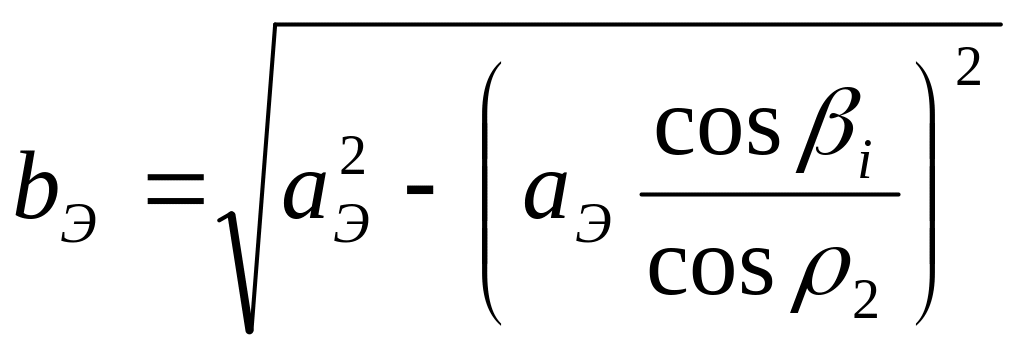 ;
;
По заданным и рассчитанным данным чертим
вид Д эллипс (сечение по
![]() ),
),
![]() .
.

![]() ;
;
Для того чтобы найти
нужно решить систему уравнений прямой
;
;
Для того чтобы найти
нужно решить систему уравнений прямой
![]() ;
уравнение прямой в общем виде:
;
и эллипса
относительно
х.
;
уравнение прямой в общем виде:
;
и эллипса
относительно
х.
;
 ;
уравнение второй степени, приведём его
к виду:
;
корнями этого уравнения будут
в точках пересечения прямой и эллипса.
;
уравнение второй степени, приведём его
к виду:
;
корнями этого уравнения будут
в точках пересечения прямой и эллипса.
;
; ; ; задача: выразить все коэффиценты через
Важно!
![]() ;
если прямая является монотонно-убывавающей
функцией,
;
если прямая является монотонно-убывавающей
функцией,
![]() - монотонно-возрастающая.
- монотонно-возрастающая.
; соответственно расположению на оси Y при Х=0 (0;0)-центр эллипса, параболы, гиперболы.
При смещении осей к коэффиценту прибавляется
;
при
;
![]() ;
;
![]() ;
;
;
;
при
![]() ;
;![]() ;
;![]() ;
;
;
-полуоси
эллипса (см. выше).
;
;
;
-полуоси
эллипса (см. выше).
-8-
Интервалы I, IV;
сечение - парабола![]()

![]() ;
;
![]() ;
;
![]() и углы
и углы
![]() ;
рассчитыаются одинаково во всех
интервалах.
;
рассчитыаются одинаково во всех
интервалах.
Каноническое уравнение параболы
![]() ;
здесь
;
здесь
![]() - элементы параболы.
- элементы параболы.
Задача - найти
![]() ;
для этого определим координаты т. Rп
;
;
для этого определим координаты т. Rп
;
![]() ;
;
По заданным и рассчитанным данным чертим
вид Дп парабола (сечение по
![]() ),
),
![]() .
.

; Для того чтобы найти нужно решить систему уравнений прямой ;
уравнение прямой в общем виде: ; и параболы относительно х
![]() ;
;
![]() ;
уравнение второй степени, приведём его
к виду:
;
корнями этого уравнения будут величины
в точках пересечения прямой и параболы.
;
уравнение второй степени, приведём его
к виду:
;
корнями этого уравнения будут величины
в точках пересечения прямой и параболы.
-9-
;
![]()
![]() ;
;
![]() ;
;
![]() ;
алгоритм расчёта
;
алгоритм расчёта
![]() и
и
![]() см. выше.
;
см. выше.
;
![]()
Интервал III;сечение -
гипербола![]()
![]() -задаваемый
параметр, центральный угол конуса.
;
;
;
и углы
;
рассчитыаются одинаково во всех
интервалах.
-задаваемый
параметр, центральный угол конуса.
;
;
;
и углы
;
рассчитыаются одинаково во всех
интервалах.

В треугольнике
![]()
![]() -большая
ось гиперболы: по теореме синусов;
-большая
ось гиперболы: по теореме синусов;
![]() ;
;![]() ;
;
;
;
![]() ;
;
 ;
;
По заданным и рассчитанным данным чертим
вид Д гипербола (сечение по
![]() ),
),
![]() .
.

-10-
;
![]() ;
Для того чтобы найти
нужно решить систему уравнений прямой
;
;
Для того чтобы найти
нужно решить систему уравнений прямой
;
уравнение прямой в общем виде:
;
и гиперболы
![]() относительно
х.
относительно
х.
![]() ;
;
 ;
уравнение второй степени, приведём его
к виду:
;
корни уравнения величины
в точках пересечения прямой и гиперболы.
;
уравнение второй степени, приведём его
к виду:
;
корни уравнения величины
в точках пересечения прямой и гиперболы.
;

 ;
;
;
;
![]() ;
задача: выразить все коэффиценты через
;
задача: выразить все коэффиценты через
![]() ;
;
![]() найдены; алгоритм расчёта
и
см. выше.
найдены; алгоритм расчёта
и
см. выше.
-
полярный радиус – переменная образующая
конуса-врезки, являющаяся гипотенузой
прямоугольного треугольника с катетами:
![]() ;
полярный угол
;
полярный угол
![]() ;
;
полярные координаты : декартовы:
-11-
V.1. Конус-тор. Оси перпендикулярны.


- находим, решая систему квадратных
уравнений прямой НдОк
и окружности
![]() ;
;
![]() ;
уравнение второй степени, приведём его
к виду:
;
;
уравнение второй степени, приведём его
к виду:
;
![]()
![]() ;
;
![]() ;
;
![]() ;
выразим все коффиценты через
;
выразим все коффиценты через
; - отрицательный, т.к. прямая НдОк при =30˚– является монотонно-убывающей функцией.
![]() .
;
.
;
![]()
корнями этого уравнения будут величины
![]() в точках пересечения прямой НдОк и круга
радиусом Rтн.
подставляем, находим корни.
в точках пересечения прямой НдОк и круга
радиусом Rтн.
подставляем, находим корни.
![]() ;
;
-12-
По заданным и рассчитанным параметрам чертим вид Д (по сечению НдОк).

Находим
![]() ;
;
![]() ;
;
Переходим к виду Г по сеч.NОт
 ΔRкр
находим, решая систему квадратных
уравнений прямой hдОт
ΔRкр
находим, решая систему квадратных
уравнений прямой hдОт![]() и окружности
;
и окружности
;
![]() ;
уравнение второй степени, приведём его
к виду:
;
уравнение второй степени, приведём его
к виду:
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]() ;
выразим все коффиценты через задаваемый
параметр
- центральный угол конуса.
;
выразим все коффиценты через задаваемый
параметр
- центральный угол конуса.
![]() ;
- положительный, т.к. прямая hдОт
при
=30˚–
является монотонно-возрастающей
функцией.
;
- положительный, т.к. прямая hдОт
при
=30˚–
является монотонно-возрастающей
функцией.
![]() .
.
![]() ;
;
корнями этого уравнения будут величины
![]() в точках пересечения прямой hдОт
и круга радиусом Rтн.
(общая
формула решения квадратных уравнений)
подставляем, находим
в точках пересечения прямой hдОт
и круга радиусом Rтн.
(общая
формула решения квадратных уравнений)
подставляем, находим
![]() .
.
Возвращаемся к виду А. Находим
![]() (отрезок
НдY), решая систему
квадратных уравнений прямой НдОк
и окружности с переменным радиусом
(отрезок
НдY), решая систему
квадратных уравнений прямой НдОк
и окружности с переменным радиусом
![]() ;
;
![]() ;
;
![]() ;
;
![]() - переменный радиус;
- переменный радиус;
