
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение высшего образовании
«МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»
Лабораторные работы
по дисциплине «Математическая логика и теория алгоритмов»
Выполнил студент
Группы УБСТ-1903
Коновалов И. А.
Вариант 7
2020
Лабораторная работа «Логические схемы»
Задание 1. По логической схеме составить логическую функцию
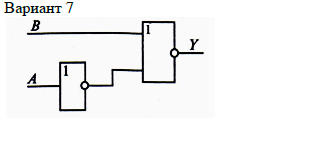
Ответ: Y = B ↓ ¬A
Задание 2. По логической схеме составить логическую функцию

Ответ: F = ⌐A ˅ A & ⌐B
Задание 3. По логической схеме составить логические функции

Ответ: Y1 = ⌐A & ⌐B ˅ A & B
Y2 = A & B
Задание 4. По логической схеме составить логическую функцию

Ответ: Y = (A | B) & C
Задание 5. По логической схеме составить логическую функцию

Ответ: F = (⌐A ˅ B) | (A | C)
Задание 6. По логической схеме составить логическую функцию

Ответ: F = A & ⌐A & B | ⌐C
Задание 7. По логической схеме составить логические функции

Ответ: Y1 = (⌐x1 ˅ ⌐x2) ˅ x3
Y2 = x1 & (x2 | x3)
Задание 8. По логической схеме составить логическую функцию
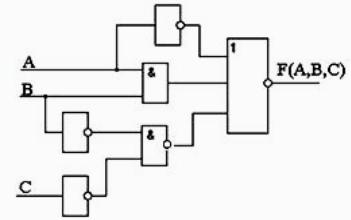
Ответ: F(A,B,C) = ⌐A ↓ A & B ↓ (⌐B | ⌐C)
Задача 9. Составить таблицу истинности логического выражения C
![]()
A |
B |
A B |
⌐(A B) |
⌐A |
(⌐A) v B |
((⌐A) v B) XOR A |
(⌐(A→B)) (((⌐A) v B) XOR A) |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
Задание 10. По логической функции составить логическую схему


Задача 11
Построить логическую схему и таблицу истинности функции F(A,B)
![]()

A |
B |
⌐A |
⌐B |
⌐A&⌐B |
⌐(⌐A&⌐B) |
AvB |
⌐(⌐A*⌐B)v(AvB) |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
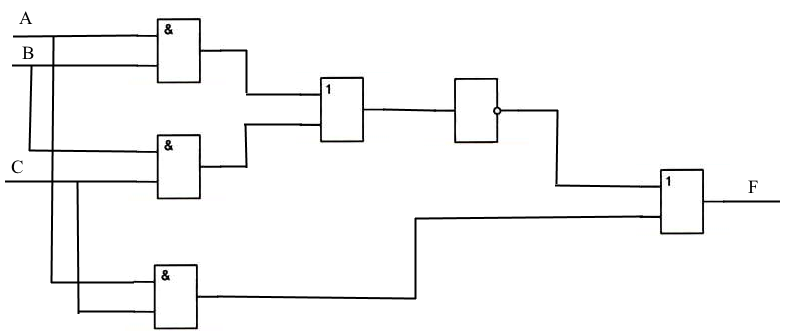
Задача 12
Построить логическую схему и таблицу истинности функции F
![]()
A |
B |
C |
A&B |
B&C |
(A&B)v(B&C) |
⌐((A&B)v(B&C)) |
A&C |
(⌐((A&B)v(B&C)))v(A&C) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Лабораторная работа 5
Моделирование простейших логических схем
Цель работы – моделирование логических функций при помощи логических элементов.
Дата 13.02.99, отбрасываем «9» получаем 13029. Переводим в двоичную систему счисления. Результат – 11001011100101. Дополняем до 16-ти разрядов. В итоге: 0011 0010 1110 0101 – это и будет результирующая функция.
x3 |
x2 |
x1 |
x0 |
f |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Задание
Реализовать полученную функцию на логических элементах
В результирующей логической функции количество единиц равно количеству нулей. Была использована совершенно дизъюнктивная нормальная форма (СДНФ).
f(x3, x2, x1, x0) = x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0 + x3 ∙ x2 ∙ x1 ∙ x0

Реализовать полученную функцию на дешифраторе
При подаче на вход дешифратора сигнала 0010, являющегося первым минтермом в СДНФ, дешифратор выдаст на выходе «2» уровень логической единицы. Затем этот сигнал поступает на лог. элемент «ИЛИ». Результатом операции будет лог.1 на выходе схемы. Выходы дешифратора, на которых при подаче других минтермов устанавливается лог.1 на выходе. Во всех остальных случаях результатом работы схемы будет лог.0.

Выполнить минимизацию по карте Карно, синтезировать схему на базисе, определенного вариантом, привести синтезируемую схему, выполнить проверку на соответствие исходной таблице истинности.
Вариант 7 – ИЛИ-НЕ
x1
x3
x2


1 |
0 |
|
1 |
|
1 |
1 |
|
1 |
0 |
|
0 |
1 |
|
0 |
0 |
f = (x3 + x2 + x1) ∙ (x3 + x1 + x0) ∙ (x3 + x0) ∙ (x2 + x0) ∙ x1
СКНФ:
f = (x3 + x2 + x1 + x0) & (x3 + x2 + x1 + ⌐x0) & (x3 + ⌐x2 + x1 + x0) & (x3 + ⌐x2 + x1 + ⌐x0) & (x3 + ⌐x2 + ⌐x1 + ⌐x0) & (⌐x3 + x2 + ⌐x1 + ⌐x0) & (⌐x3 + ⌐x2 + x1 + x0) & (⌐x3 + ⌐x2 + ⌐x1 + x0)
Подвергая минимальную КНФ двойной инверсии приводим функцию к базису ИЛИ-НЕ

 f
= f = (x3
+ x2
+ x1)
∙ (x3
+ x1
+ x0)
∙ (x3
+ x0)
∙ (x2
+ x0)
∙ x1
= a + b + c + d + e
f
= f = (x3
+ x2
+ x1)
∙ (x3
+ x1
+ x0)
∙ (x3
+ x0)
∙ (x2
+ x0)
∙ x1
= a + b + c + d + e
a = x3 + x2 + x1
b = x3 + x1 + x0
c = x3 + x0
d = x2 + x0
e = x1 = x1

Лабораторная работа 7
Структурные схемы микропроцессорных устройств, таблица соответствия: понятие, её построение по имеющейся схеме устройства
Задание 1: Получить таблицу соответствия/истинности по заданной структурной схеме микропроцессорного устройства.

Этапы решения задачи
Анализ состава и структуры входных, выходных и промежуточных сигналов. Схема содержит три логических элемента «НЕ» (), логические элементы «И» (⌐x1&⌐x2) и (⌐x2&x3), выходные сигналы которых поступают на вход логического элемента «ИЛИ», результатом работы (функционирования) которых является выходной сигнал y.
Построение логической зависимости y = f(x1, x2, x3)
Построение пустой традиционной таблицы истинности, размерность которой определяется количеством выделенных входных и выходных сигналов, а затем - пустой расширенной таблицы, размерность которой определяется количеством сечений и промежуточных переменных в них.
-
№
Вход
Промежуточные сигналы по сечениям zij
Выход
x1
x2
x3
Сечение 1
Сечение 2
Сечение 3
x1
x2
x3
z11 ⋀ z12
z12
z13
z21v z22
z22 ⋀ z23
z31v z32
z11
z12
z13
z21
z22
z23
z31
z32
y
1
…
8
Заполнение указанной расширенной таблицы истинности по сечениям путем последовательного анализа результатов воздействия входных сигналов на рассматриваемое логическое устройство с последующим получением значений выходной величины для всех комбинаций входных
Заполнение сечения 1
-
№
Вход
Промежуточные сигналы по сечениям zij
Выход
x1
x2
x3
Сечение 1
Сечение 2
Сечение 3
x1
x2
x3
z11 ⋀ z12
z12
z13
z21v z22
z22 ⋀ z23
z31v z32
z11
z12
z13
z21
z22
z23
z31
z32
y
1
0
0
0
1
1
0
2
0
0
1
1
1
1
3
0
1
0
1
0
0
4
0
1
1
1
0
1
5
1
0
0
0
1
0
6
1
0
1
0
1
1
7
1
1
0
0
0
0
8
1
1
1
0
0
1

 1
1 0
0 0
0 0
0 1
1