
- •1 Исследование однофазных выпрямителей
- •Ознакомление с комплектом типового лабораторного оборудования
- •Общие сведения
- •Компоновка оборудования
- •Блок генераторов напряжений с наборным полем
- •Набор миниблоков
- •Блок мультиметров
- •Ваттметр
- •Лабораторная работа № 1
- •Введение
- •Экспериментальная часть Задание
- •Порядок выполнения работы
- •Вопросы к допуску для выполнения работы
- •Контрольные вопросы к защите работы
- •Лабораторная работа № 2
- •Введение
- •Экспериментальная часть Задание
- •Порядок выполнения эксперимента
- •Вопросы к допуску для выполнения работы
- •Контрольные вопросы к защите работы
- •Лабораторная работа № 3
- •Введение
- •Экспериментальная часть Задание
- •Порядок выполнения работы
- •Вопросы и задания к допуску для выполнения работы
- •Контрольные вопросы к защите работы
- •Лабораторная работа № 4
- •Экспериментальная часть Задание
- •Порядок выполнения эксперимента
- •Лабораторная работа № 5 Исследование трёхфазной цепи при соединении нагрузки в звезду
- •Введение
- •Экспериментальная часть Задание
- •Порядок выполнения эксперимента
- •Векторные диаграммы
- •3. Смешанная несимметричная нагрузка фаз:
- •Вопросы к допуску для выполнения работы
- •Контрольные вопросы к защите работы
- •Лабораторная работа № 6 Исследование трехфазной цепи при соединении нагрузки в треугольник
- •Общие сведения
- •Экспериментальная часть Задание
- •Порядок выполнения эксперимента
Вопросы к допуску для выполнения работы
1. Какая цепь называется неразветвленной?
2. Какие проводятся измерения в этой цепи?
3. Какие осциллограммы рассматриваются в изучаемой цепи? Как их получить практически на экране осциллографа?
4. Сформулируйте условия резонанса в неразветвленной цепи. По каким измерениям и осциллограммам можно установить, что в цепи возник резонанс? Каковы при этом фазовые соотношения между напряжениями?
5. Как по показаниям приборов судить о том, какое реактивное сопротивление в цепи преобладает: индуктивное или емкостное?
6. Как надо изменить емкость, чтобы приблизиться к резонансу, если ток в контуре отстает по фазе от приложенного к контуру напряжения?
Контрольные вопросы к защите работы
1. Временное, комплексное и векторное представление гармонических колебаний.
2. Что такое мгновенная, средняя, активная, реактивная и полная мощности переменного тока?
3. Цепь переменного тока с резистором. Полное сопротивление цепи. Фазовые соотношения между током и напряжением, активная мощность.
4. Комплексное сопротивление цепи, содержащей реальную индуктивность. Фазовые соотношения между током и напряжением, мощности.
5. Конденсатор в цепи переменного тока. Комплексное сопротивление этой цепи. Фазовые соотношения между током и напряжением, мощность.
6. Закон Ома для неразветвленной цепи переменного тока, полное сопротивление неразветвленной цепи, содержащей R, L, C.
7. Как строятся векторные диаграммы последовательной цепи и треугольник сопротивлений?
8. Что такое резонанс напряжений в последовательной цепи?
9.
Объясните характер зависимостей I,
UR,
UL,
UC от С.
от С.
10. Приведите формулировку второго закона Кирхгофа.
11. Выполнение второго закона Кирхгофа в цепи (рис.9)?
Лабораторная работа № 2
РАЗВЕТВЛЕННЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Цель работы: исследование электрической цепи переменного тока, состоящей из параллельно включенных реактивных элементов (катушки индуктивности, конденсатора) и резистора. Анализ явления резонанса токов в параллельном колебательном контуре. Проверка первого закона Кирхгофа.
Литература: [1] Глава 1: §§ 1.1 – 1.5, §1.7; [2] Глава I: §§ 1.1 – 1.17; [3] Глава первая §§ 1.1 – 1.11, 1.14 – 1.18
Введение
Для нормальной работы приемников
электрической энергии (нагревательных
и осветительных приборов, электродвигателей,
телевизоров и др.) их необходимо подключить
к сети с определенным напряжением U.
Обычно
 .
Чтобы обеспечить необходимое напряжение
на входе каждого приемника, все приемники
должны быть включены параллельно. Цепь,
в которой имеются разветвления и
параллельные пути протекания токов,
называется разветвленной.
.
Чтобы обеспечить необходимое напряжение
на входе каждого приемника, все приемники
должны быть включены параллельно. Цепь,
в которой имеются разветвления и
параллельные пути протекания токов,
называется разветвленной.
Токи, протекающие через различные приемники энергии, определяются сопротивлениями этих приемников и приложенным к ним напряжением и, как правило, различаются. Мгновенное значение тока в общем проводе цепи в соответствии с 1-м законом Кирхгофа равно сумме мгновенных значений токов, протекающих через различные приемники:
 ,
(1)
,
(1)
а комплексная амплитуда тока
 в общем проводе равна сумме комплексных
амплитуд токов в отдельных ветвях
схемы:
в общем проводе равна сумме комплексных
амплитуд токов в отдельных ветвях
схемы:
 (2)
(2)
При этом амплитуда общего тока
 не равна сумме амплитуд токов
не равна сумме амплитуд токов
 из-за различия фаз колебаний токов
из-за различия фаз колебаний токов
 .
Амплитуда тока в общем проводе равна
модулю суммы комплексных амплитуд токов
в отдельных параллельных ветвях схемы:
.
Амплитуда тока в общем проводе равна
модулю суммы комплексных амплитуд токов
в отдельных параллельных ветвях схемы:
 (3)
(3)
Каждый из параллельно включенных
приемников характеризуется соответствующим
сопротивлением
 .
Если известно комплексное сопротивление
цепи
.
Если известно комплексное сопротивление
цепи
 ,
то комплексная проводимость есть
величина, обратная комплексному
сопротивлению:
,
то комплексная проводимость есть
величина, обратная комплексному
сопротивлению:
 (4)
(4)
Она измеряется в сименсах (См).
Комплексная проводимость разветвленной цепи равна сумме комплексных проводимостей отдельных параллельно включенных приемников:
 , (5)
, (5)
где
 .
.
Величины комплексных проводимостей
для резистора, идеальной катушки
индуктивности (у которой
 )
и конденсатора определяются из соотношений
между комплексными амплитудами тока и
напряжения на этих элементах и
соответственно равны:
)
и конденсатора определяются из соотношений
между комплексными амплитудами тока и
напряжения на этих элементах и
соответственно равны:
 (6)
(6)
В случае неидеальной катушки индуктивности
( ),
активная (
),
активная ( )
и реактивная (
)
и реактивная ( )
составляющие проводимости катушки
)
составляющие проводимости катушки
 соответственно равны:
соответственно равны:
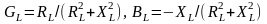
Комплексная проводимость определяет комплексную амплитуду тока при заданной комплексной амплитуде напряжения или комплексную амплитуду напряжения по комплексной амплитуде тока (по закону Ома)
 (7)
(7)
Связь между действительными амплитудами тока и напряжения определяется формулой:
 ,
где
,
где
 (8)
(8)
Связь между начальными фазами колебаний тока и напряжения имеет вид:
 ,
где
,
где
 (9)
(9)
В параллельной цепи, содержащей
индуктивные и емкостные приемники,
возможно возникновение явления, когда
суммарный общий ток определяется только
активной
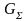 проводимостью цепи, а напряжение на
входе и общий ток цепи совпадают по
фазе. Этот режим работы цепи называют
резонансом токов. В этом случае реактивные
составляющие токов индуктивной и
емкостной ветвей цепи равны по величине
и противоположны по фазе, т.е. происходит
обмен энергией между емкостью и
индуктивностью. Реактивные составляющие
токов компенсируются в общем проводе
цепи. В этом режиме цепь представляет
активный двухполюсник, эквивалентная
проводимость которого равна сумме
активных проводимостей ветвей. Коэффициент
мощности
проводимостью цепи, а напряжение на
входе и общий ток цепи совпадают по
фазе. Этот режим работы цепи называют
резонансом токов. В этом случае реактивные
составляющие токов индуктивной и
емкостной ветвей цепи равны по величине
и противоположны по фазе, т.е. происходит
обмен энергией между емкостью и
индуктивностью. Реактивные составляющие
токов компенсируются в общем проводе
цепи. В этом режиме цепь представляет
активный двухполюсник, эквивалентная
проводимость которого равна сумме
активных проводимостей ветвей. Коэффициент
мощности
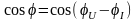 при этом достигает максимально возможной
величины (равной единице). Следует
отметить, что в случае резонанса токи,
протекающие через реактивные элементы,
могут быть значительно больше тока,
протекающего через общий провод.
при этом достигает максимально возможной
величины (равной единице). Следует
отметить, что в случае резонанса токи,
протекающие через реактивные элементы,
могут быть значительно больше тока,
протекающего через общий провод.
Модуль полной мощности S равен:
 ,
,
где
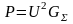 – активная мощность [Вт],
– активная мощность [Вт],
 – реактивная мощность [ВАР]. Соотношение
между полной S и
активной P мощностями
описывается формулой
– реактивная мощность [ВАР]. Соотношение
между полной S и
активной P мощностями
описывается формулой
 .
Полная S и реактивная
Q мощности связаны
формулой
.
Полная S и реактивная
Q мощности связаны
формулой
 .
.
Большинство потребителей энергии переменного тока (особенно электрические двигатели и трансформаторы) проявляют себя как индуктивно-активные нагрузки. Если заданы напряжение U и активная (полезная) мощность Р потребителя, то ток потребителя зависит от cos. С уменьшением cos потребителя его ток возрастает:
 (10)
(10)
Это, в свою очередь, приводит к увеличению мощности потерь в линии передачи электрической энергии от источника к потребителю и в самом источнике энергии. Если сопротивление проводов этой линии r, то мощность потерь в ней
 (11)
(11)
Как видно из этого выражения, мощность
потерь тем больше, чем ниже cos
установки. Снизить ток в общей цепи
можно за счет уменьшения реактивного
тока, носящего индуктивный характер,
что может быть достигнуто путем
параллельного подключения к питающей
сети емкостной нагрузки (батареи
конденсаторов). При этом токи, протекающие
через индуктивную проводимость ( )
и емкостную проводимость (
)
и емкостную проводимость ( )
противофазны, т. е. различаются по фазе
на , и компенсируют
друг друга в общем проводе, а общий ток
определяется активной проводимостью
установки.
)
противофазны, т. е. различаются по фазе
на , и компенсируют
друг друга в общем проводе, а общий ток
определяется активной проводимостью
установки.
Если катушка, обладающая индуктивностью L и активным сопротивлением R соединена параллельно с конденсатором ёмкостью С (рис.3.2а), то напряжение на них одно и то же, а ток I на входе цепи представляет сумму тока в катушке Iк, отстающим от напряжения на угол , и тока в конденсаторе IС, опережающего напряжение на 90о.

Рис.3.1
Для сложения токов сначала представим ток в катушке в виде двух составляющих: активной Iка, и реактивной Iкр, как показано на рис.3.2б, а затем нарисуем из конца вектора Iкр вектор тока в конденсаторе (рис. 3.2.в), опережающий напряжение на 90о и получим суммарный ток. Из векторной диаграммы следует, что

где

 -
полная проводимость этой цепи.
-
полная проводимость этой цепи.
В свою очередь:
 - реактивная проводимость всей цепи;
- реактивная проводимость всей цепи;
BL = Yкsinк – индуктивная проводимость катушки;
BC = C – ёмкостная проводимость конденсатора;
G = Yкcosк - активная проводимость катушки;
Из векторной диаграммы следует также, что угол сдвига между током и напряжением
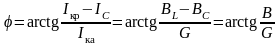 .
.
Если ВL>ВC, то угол положительный и напряжение опережает ток. Этот случай показан на векторной диаграмме сплошными линиями. Если же ВL<ВC, то угол отрицательный, и напряжение отстаёт от тока (показано на векторной диаграмме пунктиром). Если же, наконец, ВL=ВC, тогда и Iкр = IC и = 0, и ток совпадает с напряжением по фазе. Этот случай называется резонансом токов.
Условие резонанса BL = BC или = 0 можно также записать в виде:
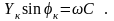
В свою очередь,
 ,
поэтому
,
поэтому

Отсюда можно определить ёмкость, индуктивность или частоту, при которой в цепи будет наблюдаться резонанс.
