Лабораторная работа № 1

НЕРАЗВЕТВЛЕННЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Цель работы: исследование свойств электрической цепи с последовательным соединением катушки индуктивности, конденсатора и резистора, а также явле­ния резонанса напряжений в после­довательном колебательном контуре. Проверка второго закона Кирхгофа в векторной форме.

Литература: [1] Глава 1: §§ 1.1 – 1.6; [2] Глава I: §§ 1.1 – 1.17; [3] Глава первая §§ 1.1 – 1.13, 1.15,1.16, 1.18.

Введение

Неразветвленной цепью называется цепь, все элементы которой включены последовательно, а разветвления – параллельные пути протекания тока отсутствуют. При этом через все элементы неразветвленной цепи протекает одинаковый ток. Последовательная цепь переменного тока может содержать как элементы с активным сопротивлением R (резисторы, реостаты), так и элементы с реактивным сопротивлением X (катушки индуктивности, конденсаторы). В элементах и устройствах, характеризующихся активным сопротивлением, электрическая энергия безвозвратно преобразуется в тепло, или в механическую энергию, или в электромагнитную энергию. В элементах с реактивным сопротивлением нет безвозвратных потерь энергии, в них происходит в течение каждого периода накопление (в виде электрической энергии в конденсаторах и магнитной энергии в катушках индуктивности) и возврат накопленной энергии в цепь.

Если к входу такой цепи приложить переменное напряжение

(1)

то через все элементы неразветвленной цепи потечет один и тот же переменный ток i (t). В формуле (1): – амплитуда напряжения (максимальное значение напряжения); – угловая частота (рад/с) ( , – частота колебаний (Гц), т.е. количество полных колебаний за 1 сек.); – текущее время (с); – начальная фаза колебаний (рад); – мгновенная фаза (рад).

В соответствии со 2-м законом Кирхгофа мгновенное значение напряжения на входе этой цепи будет равно сумме мгновенных напряжений на ее элементах:

(2)

Переменное напряжение (и ток) кроме временного представления (1) может быть также выражено в виде комплексного представления и записано в показательной форме:

(3)

т. е. мгновенное значение переменного напряжения равно действительной части произведения комплексной амплитуды и оператора вращения . Комплексная амплитуда общего напряжения , приложенного к входу цепи, в соответствии со вторым законом Кирхгофа равна сумме комплексных амплитуд напряжений на ее элементах:

(4)

при этом амплитуда общего напряжения не равна сумме амплитуд . Из-за различия фаз колебаний напряжений 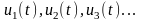амплитуда общего напряжения равна модулю суммы комплексных амплитуд напряжений на элементах электрической цепи

(5)

Неразветвленная электрическая цепь последовательно соединенных элементов с активным R и реактивным X сопротивлениями характеризуется полным комплексным сопротивлением , которое равно сумме комплексных сопротив­лений отдельных элементов и может быть представлено в алгебраической форме

(6)

или в показательной форме

, (7)

где: - соответственно суммы активных и реактивных сопротивлений цепи; - модуль комплексного сопротивления или полное сопротивление цепи; - аргумент комплексного сопротивления цепи .

Величины комплексных сопротивлений для резистора, идеальной катушки индуктивности и идеального конденсатора определяются из соотношений между комплексными амплитудами напряжения и тока на этих элементах:

(8)

Реальная катушка индуктивности характеризуется индуктивным сопротивлением 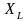и активным сопротивлением , определяемым активным сопротивлением провода катушки, зависящим от диаметра, длины и материала провода. Полное комплексное сопротивление катушки индуктивности равно .

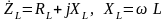Активными потерями в конденсаторе, как правило, пренебрегают вследствие их малости, поэтому его комплексное сопротивление реактивно: , .

Зная действительную 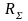и мнимую части комплексного сопротивления всей цепи, можно построить треугольник сопротивлений с катетами равными и _. Длина гипотенузы этого треугольника равна модулю комплексного сопротивления . По комплексному сопротивлению цепи в соответствии с законом Ома можно определить комплексную амплитуду напряжения по комплексной амплитуде тока (или комплексную амплитуду тока при заданной комплексной амплитуде напряжения):

(9)

Отсюда легко найти связь между действительными амплитудами тока и напряжения

(10)

и начальными фазами колебаний напряжения и тока

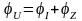(11)

При измерениях и расчетах следует иметь в виду, что шкалы измерительных приборов (вольтметров и амперметров) проградуированы не в амплитудных, а в действующих значениях напряжения и тока, равных , . Под действующим значением переменного напряжения (тока) понимается такое значение постоянного напряжения (тока), которое эквивалентно по энергии, выделяемой за период переменным напряжением (током).

Величина

[ВА] (12)

называется полной мощностью.

Активная мощность цепи определяется формулой:

[Вт] (13)

Важной характеристикой цепи является коэффициент мощности , показывающий какую часть от полной мощности составляет активная мощность . Коэффициент мощности равен отношению активной мощности Р к полной S и является косинусом угла сдвига фаз между приложенным к цепи напряжением и током, протекающим в ней:

(14)

Режим работы цепи, при котором в последовательной цепи, состоящей из элементов R, L, C, фаза общего напряжения цепи совпадает с фазой тока (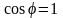 ), называют резонансом напряжений. Резонанс напряжений возникает в последовательном колебательном контуре, содержащем кроме R также L и C элементы, когда индуктивное и емкостное напряжения компенсируют друг друга ( ), так как они равны по величине и противоположны по фазе, а суммарное реактивное сопротивление равно нулю (X = 0). При этом индуктивное сопротивление катушки равно по модулю емкостному сопротивлению конденсатора ( ), а комплексное сопротивление контура носит активный характер.

При резонансе напряжений происходит периодический обмен энергией между емкостью и индуктивностью, общий ток в цепи максимален и определяется только общим активным сопротивлением цепи . Напряжения на реактивных элементах могут существенно превышать входное напряжение и могут стать опасными!