ЛАБОРАТОРНАЯ РАБОТА № 4
Мультиплексоры и их использование
Цель работы: |
Исследовать схемы мультиплексоров на логических элементах и в интегральном исполнении. Использовать мультиплексоры для реализации переключательных функций. |
Краткие теоретические сведения
Мультиплексор – комбинационная схема с несколькими входами и одним выходом. На выход мультиплексора передается информация с одного из пронумерованных входов. Номер входа, с которого данные поступают на выход, определяется комбинацией на управляющих (адресных) входах мультиплексора. Работу мультиплексора с n входами можно описать уравнением
, (1)
где
-
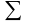знак логической суммы (дизъюнкция),
-
минтермы, определяющие комбинацию на
адресных входах,
-
входы данных.
Например, уравнение для мультиплексора с двумя входами данных (B и D) и одним адресным входом (А), согласно (1), записывается так
.
Мультиплексоры различаются по числу (N) входов данных
,
г
де
n
– количество адресных входов и записывают
"мультиплексор N-1".
Схема мультиплексора 2-1 (читается "два
в один") показана на рис.1.4.
Рис.1.4
В
интегральном исполнении выпускается
микросхема, содержащая четыре
мультиплексора 2-1 (533КП16). Схема включения
американского аналога 74157 показана на
рис.2.4
Рис.2.4
Уравнение для мультиплексора 4-1 можно записать следующим образом
, (2)
где A,B – адресные входы, 0, 1, 2, 3 – входы данных.
С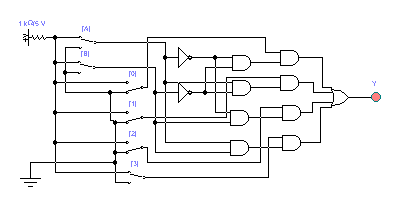
хема
мультиплексора 4-1, реализующая уравнение
(2), показана на рис.3.4.
Рис.3.4
В
интегральном исполнении выпускается
два мультиплексора 4-1 в одной микросхеме
(155КП2). Схема включения американского
аналога 74153 показана на рис.4.4.
Рис. 4.4.
Т
акже
в интегральном исполнении выпускаются
мультиплексоры 16-1 и 8-1, соответственно
микросхемы 155КП1 и 155КП7. Схемы их
американских аналогов 74150 и 74151 показаны
на рис.5.4.
Рис. 5.4.
Мультиплексоры находят широкое применение в цифровой технике. Они используются для межразрядных связей в регистрах, счетчиках, для реализации переключательных функций.
Рассмотрим реализацию функции четырех переменных на различных типах мультиплексоров.
Пусть функция задана числовым способом:
y
= ∑(3, 4, 5, 11, 12, 13, 14).
Запишем для этой функции таблицу истинности (табл.1).
Подадим входные сигналы на адресные входы (A=x0, B=x1, C=x2, D=x3).
Таблица 1.
№ |
x3 |
x2 |
x1 |
x0 |
y |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
3 |
0 |
0 |
1 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
1 |
6 |
0 |
1 |
1 |
0 |
0 |
7 |
0 |
1 |
1 |
1 |
0 |
8 |
1 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
0 |
10 |
1 |
0 |
1 |
0 |
0 |
11 |
1 |
0 |
1 |
1 |
1 |
12 |
1 |
1 |
0 |
0 |
1 |
13 |
1 |
1 |
0 |
1 |
1 |
14 |
1 |
1 |
1 |
0 |
1 |
15 |
1 |
1 |
1 |
1 |
0 |