
РГРки https vk.com a777big / РГР 1 Сергеев А.С. 5А07
.pdf
Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования
«Национальный исследовательский Томский политехнический Университет»
Школа: Инженерная школа энергетики Направление: Электроэнергетика и электротехника Отделение: ОЕН ШБИП
Теоретические основы электротехники 1.1
Расчетно-графическая работа №1 «Линейные электрические цепи с постоянными напряжениями и токами»
Вариант №986
Исполнитель: |
|
|
студент группы |
5А07 |
Сергеев А.С. |
Руководитель: |
|
|
преподаватель |
|
Васильева О.В |
Томск – 2022
Задание:
Для заданной схемы с постоянными во времени источниками ЭДС
итока, принимая e1(t) = E, e2 (t) = E2, e3 (t) = 0, J (t) = J, выполнить следующее.
1.Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления.
2.Определить токи во всех ветвях схемы и напряжение на зажимах источника тока:
• |
по законам Кирхгофа, |
• |
методом контурных токов, |
• |
методом узловых потенциалов. |
3. |
Составить баланс вырабатываемой и потребляемой мощностей. |
4. |
Определить ток в ветви ab: |
• |
методом наложения, |
• |
методом преобразований. |
5.Рассматривая цепь относительно сопротивления R ветви ab как активный двухполюсник, заменить его эквивалентным генератором, определить параметры эквивалентного генератора и рассчитать ток в ветви ab, построить внешнюю характеристику эквивалентного генератора и по ней графически определить ток в ветви ab.
6.Для любого контура без источника тока построить потенциальную диаграмму.
7.Определить показание вольтметра.
8.Сравнить результаты вычислений, оценить трудоемкость методов расчета и сформулировать выводы по выполненным пунктам задания.
Дано:
E1 |
E2 |
α1 |
α2 |
J |
β |
R |
L |
C |
|
|
|
|
|
|
|
|
|
В |
В |
Град |
Град |
А |
Град |
Ом |
мГн |
мкФ |
|
|
|
|
|
|
|
|
|
190 |
120 |
210 |
60 |
3 |
0 |
80 |
254,78 |
39,8 |
|
|
|
|
|
|
|
|
|
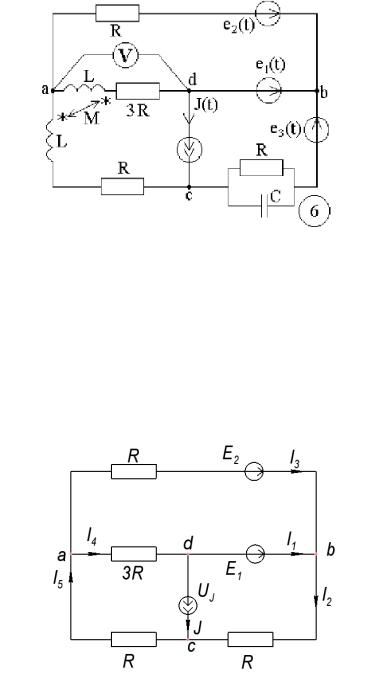
Схема:
Рис. 1 Исходная схема.
1. Изображаем схему, достаточную для расчета постоянных токов ветвей, соединяющих узлы, помеченные буквами. При этом учитываем, что индуктивный элемент L для постоянного тока является «закороткой», а емкостный элемент C при постоянном напряжении представляет собой «разрыв» ветви, причем взаимная индуктивность M влияния на постоянные токи не оказывает. Указываем произвольно номера и направления токов в ветвях схемы. Данная схема имеет: nу = 4 узла, nв =6 ветвей, nI =5 неизвестных токов.
Рис. 2 Преобразованная схема
2. Определяем токи во всех ветвях схемы и напряжение на зажимах источника тока.
2.1. Используем законы Кирхгофа.
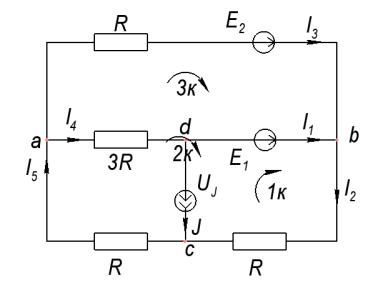
Рис. 3 Обозначение контуров Рассчитаем число уравнений, которые необходимо составить:
1 = у − 1 = 3 уравнений по первому закону Кирхгофа,
2 = в − 1 = 3 уравнений по второму закону Кирхгофа.
Выбираем три узла (например, a, b, с) и составляем уравнения по первому закону Кирхгофа:
узел a: −3 − 4 + 5 = 0; узел b: 3 − 2 + 1 = 0; узел с: − 5 + 2 = 0.
Для трех контуров составляем уравнения по второму закону Кирхгофа:
1контур (c-d-b-c): 2 ∙ = 1 −
2контур (a-d-b-c-a): 4 ∙ 3 + 2 ∙ + 5 ∙ = 1
3контур (a-b-d-a): 3 ∙ − 4 ∙ 3 = 2 − 1
Полученные уравнения записываем в программе MathCad и решаем с помощью команды Given-Find:

Рис. 4 Расчет в MathCad
По результатам расчетов получаем значения:
1 = −2,352
2 = −1,284
3 = 1,068
4 = 0,648
5 = 1,716
= 292,727 В
Сделаем проверку:
Узел a: − 3 − 4 + 5 = (−1,068 − 0,648 + 1,716) = 0
1 контур: 2 ∙ = −1,284 ∙ 80 = −102,72 = 1 − = 190 − 292,72 = −102,72
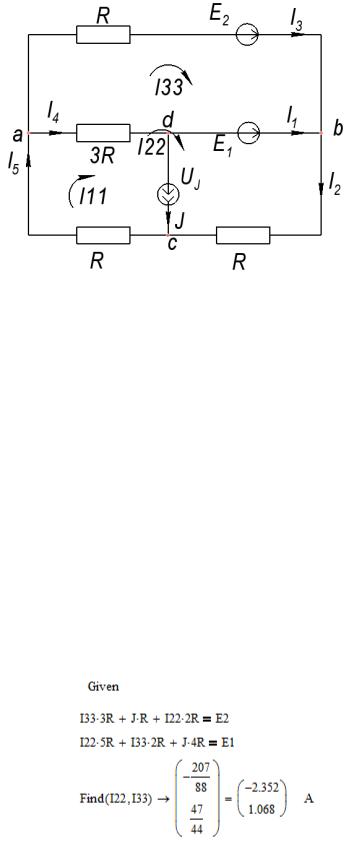
2.2. Используем метод контурных токов.
Рис. 5 Схема с изображением контурных токов.
Рассчитываем число контурных токов, которые необходимо направить в схеме nкт nв ny 1 3 и число контурных уравнений, которые необходимо
будет решить nку nI ny 1 2 .
Обозначаем ку = 3 контурных тока как I11, I22 , I33 и направляем их в
независимых контурах, которые отличаются друг от друга наличием хотя бы одной новой ветви, причем, через источник тока должен проходить один контурный ток, например, 11, тогда 11 = (контур adca). Для двух неизвестных контурных токов I22 и I33 составляем 2 уравнения:
I22 (контур adbca): 22 ∙ (3 + + ) + 33 ∙ ( + ) + 11 ∙ (3 + ) = 1
для I33 (контур acba): 33 ∙ ( + + ) + 11 ∙ + 22 ∙ ( + ) = 2
Полученные уравнения записываем в программе MathCad и решаем с помощью команды Given-Find:
Рис. 6 Расчет в MathCad
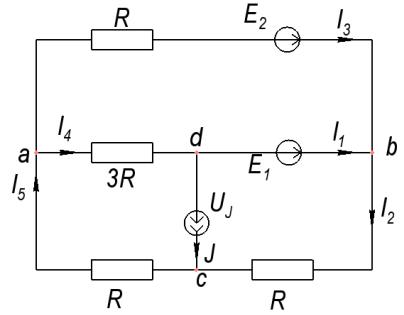
Далее находим реальные токи и напряжение в ветвях схемы с учетом контурных токов, проходящих в этих ветвях:
1 = 22 = −2,3522 = 22 + 33 = −2,352 + 1,068 = −1,2843 = 33 = 1,068
4 = 22 + 11 = −2,352 + 3 = 0,6485 = 22 + 11 + 33 = −2,352 + 3 + 1,068 = 1,716
Напряжение найдем по второму закону Кирхгофа для первого контура:
5 ∙ + 4 ∙ 3 =
= 1,716 ∙ 80 + 0,648 ∙ 3 ∙ 80 = 292,8 В
Найденные токи в ветвях схемы и напряжение на зажимах источника тока совпадают с результатами п. 2.1.
2.3. Используем метод узловых потенциалов.
Рис. 7 Схема с обозначением узлов
Потенциал одного из узлов принимаем равным нулю. Таким узлом будет один из узлов ветви без сопротивления, например, φd=0. Тогда учитывая находим
1 = − ; = + 1 = 190
Для неизвестных потенциалов и составляем расчетные уравнения:

Для : (1 + 31 + 1) ∙ − 1 ∙ − 1 ∙ = − 2
Для : (1 + 1) ∙ − (∞1 ) ∙ − 1 ∙ − 1 ∙ =
Рис. 8 Расчет в MathCad
Получим результат:
=155,455 В
=292,727 В
Далее используем обобщенный закон Ома и первый закон Кирхгофа:
I2 |
= |
φb−φc |
= |
|
190−292,727 |
= −1,284 A |
||||||||
|
|
80 |
|
|||||||||||
|
|
R |
|
|
|
|
||||||||
I3 |
= |
φa−φb+E2 |
= |
155,455−190+120 |
= 1,068 A |
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
R |
80 |
|
|
|||||||||
I4 |
= |
φa−φd |
= |
|
|
155,455−0 |
= 0,648 A |
|||||||
|
|
|
|
|||||||||||
|
|
3R |
|
|
|
3∙80 |
||||||||
I5 |
= |
φс−φa |
= |
292,727−155,455 |
= 1,716 A |
|||||||||
|
|
|||||||||||||
|
|
R |
80 |
|
|
|
|
|||||||
I1 = I2 − I3 = −1,284 − 1,068 = −2,352 A
UJ = φc − φd = 292,727 − 0 = 292,727 В
Таким образом, найденные токи и напряжение на зажимах источника тока совпадают с результатами п. 2.1. и п. 2.2.
3. Для проверки правильности расчетов составляем баланс вырабатываемой Pв и потребляемой Pп мощности. Так же рассчитываем допустимую относительную погрешность (δ) расчетов:
в = 1 1 + 2 3 + = 559,5 Вт
= 22 + 32 + 3 42 + 52 = 561,6 Вт
|
| − | |
|
|559,5−561,6| |
|
|
= |
в |
∙ 100% = |
|
|
∙ 100% = 0,375% |
|
559,5 |
|
|||
|
|
|
|
||
|
в |
|
|
|
|
4. Определяем ток в ветви ab.
4.1. Используем метод наложения.
Для расчета тока 3, который протекает в ветви ab, исходную схему с постоянными токами разобьем на три подсхемы с одним источником ЭДС или тока.
4.1.1. Расчет подсхемы с ЭДС 2.
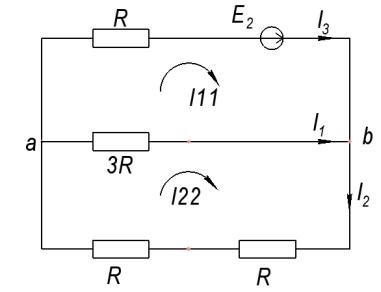
Рис. 9 Подсхема с ЭДС 2.
По методу контурных токов составляем два уравнения и считаем ток в ветви ab:
Первый контур: 11 ∙ ( + 3 ) − 22 ∙ 3 = 2
Второй контур: 22 ∙ ( + + 3 ) − 11 ∙ 3 = 0
Записываем уравнения в MathCad и производим вычисления:
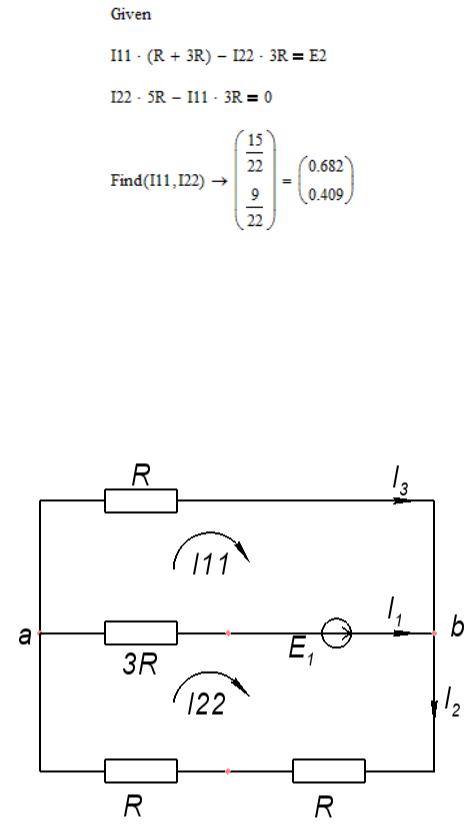
Рис. 10 Расчет контурных токов
Ток в ветви ab вычислим по имеющимся значениям контурных токов:
2 = 11 = 0,682
4.1.2. Расчет подсхемы с ЭДС 1.
Рис. 11 Подсхема с ЭДС 1.
По методу контурных токов составляем два уравнения и считаем ток в ветви ab:
Первый контур: 11 ∙ ( + 3 ) − 22 ∙ 3 = −1
