МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра биотехнических систем

ОТЧЕТ

по лабораторной работе №2

по дисциплине «Теория случайных процессов»

Тема: Белый шум и случайные блуждания

Вариант 4

Студентки гр. 0502	Лиоско Е.П. Потько А.А.
Преподаватель	Скоробогатова А.И.

Санкт-Петербург

2022

Цель: изучение концепций, лежащих в основе теории случайных процессов и получение навыков генерирования случайных блужданий и белого шума.

Теоретические сведения

1.Белый шум

Случайный процесс в дискретном времени – это последовательность случайных переменных. Случайный процесс ξ(t) имеет две размерности; переменная t принимает значения 0, 1, 2,..., при которых реализация выбирается из непрерывного пространства состояний в соответствии с распределением. Простейшим случайным процессом является белый гауссовский шум, который представляет собой последовательность некоррелированных случайных переменных с нормальным распределением. Для демонстрации двумерной природы случайного процесса мы можем представить матрицу, размерности N на K, где N – кол-во строк, или количество раз, когда мы запускаем случайный процесс. K - столбцов, каждое k-ое значение в нем – результат функции normrnd - сколько раз величина меняла свое значение в ходе N-ого процесса. Предположив, что случайная величина меняет свое значение каждую единицу времени один раз, то K – будет и временем случайного процесса, и общим кол-вом реализаций k. Каждое значение за один запуск будет называться реализацией, совокупность этих значений – последовательностью, все вместе – выборкой:

Таким образом, n -ая строка содержит K различных реализаций выборки ξ [n], где столбец k – это одна реализация всей последовательности {ξ [1],..., ξ [N]}, индексируемой номером реализации k .

Мы можем рассчитать среднее по ансамблю (средние значение каждой N-ой строчки):

А также среднее по времени для k-й реализации (среднее значение каждого K-ого столбца):

В ажной концепцией случайных процессов является эргодичность, которая означает, что статистические характеристики случайного процесса, полученные в ходе усреднения по времени, равны полученным при усреднении по ансамблю. Для этого необходимо, чтобы μ_ξ [n] = μ_ξ независимо от n, и независимо от k. Эргодичность связана со стационарностью в широком смысле.

Важной характеристикой случайного процесса является выборочная корреляция по ансамблю:

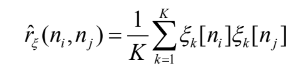
Мы называем ее «выборочной», поскольку K конечно, настоящее среднее по ансамблю r_ξ (n_i,n_j ) =M [ξ(n_i)ξ(n_j)] будет получено при K → ∞.

Также важное значение играет нормированный коэффициент корреляции:

2.Случайные блуждания (винеровский процесс)

Для задания процесса со случайными блужданиями необходимо рекурсивно генерировать последовательность:

П оложим, мы имеем дискретную случайную величину X, которая принимает конечное или счетное число значений {x_i}, i = 1,2,..., n с вероятностями p_i =P {X = x_i }, (в общем случае, n может быть равно ∞).

3.Случайные блуждания с затуханием

Случайные блуждания с поглощением являются стационарным случайным процессом и могут быть заданы следующим выражением:

Так как данный процесс является стационарным для больших значений n, среднее по времени должно быть равно среднему по ансамблю. Тогда автокорреляция может быть рассчитана по одной реализации:

Ход работы

1. Белый шум

Текст программы

clc

clear all

close all

%1 этап - белый гауссовский шум

m = zeros(400,800);

for i = 1:400%генерируем матрицу с К случайными процессами

for j = 1:800

m(i,j) = normrnd(8,2);

end

end

%1.1 этап - расчет среднего по ансамблю

ansl = zeros(1,400);

for i = 1:400

ansl(1,i) = mean(m(i,:)); %двоеточие включает все индексы строки

end

%1.2 этап - расчет среднего по времени для k-й реализации

sr = zeros(1,800);

for i = 1:800

sr(1,i) = mean(m(:,i));

end

figure('Name','График среднего по ансамблю','NumberTitle','off','Position',[0,380,1000,400])

plot(ansl)

hold on

plot(sr)

xlim([0 400]);

clear ansl sr

%2 этап - диаграммы рассеяния

figure('Name','Диаграммы рассеяния','NumberTitle','off','Position',[600,0,1000,400])

subplot(1,3,1)

rass = randi(800,3,2);

r(1,:) = xcorr(m(:,rass(1,1)),m(:,rass(1,2)),1,'normalized');%откорректированная матрица, в скобках случайно сгенерированные значения

r(2,:) = xcorr(m(:,rass(2,1)),m(:,rass(2,2)),1,'normalized');%1 - максимальный размер

r(3,:) = xcorr(m(:,rass(3,1)),m(:,rass(3,2)),1,'normalized');%полученные значения отражают коррелированность случайных величин

scatter(m(:,rass(1,1)),m(:,rass(1,2)),10,'g');%рисуем маркеры

legend ('Первое значение')

hold on

subplot(1,3,2)

scatter(m(:,rass(2,1)),m(:,rass(2,2)),10,'b');

legend ('Второе значение')

hold on

subplot(1,3,3)

scatter(m(:,rass(3,1)),m(:,rass(3,2)),10,'m');

legend ('Третье значение')

hold on

xlim([-20 50])

ylim([-20 50])

clear m i j r rass

Окна вывода

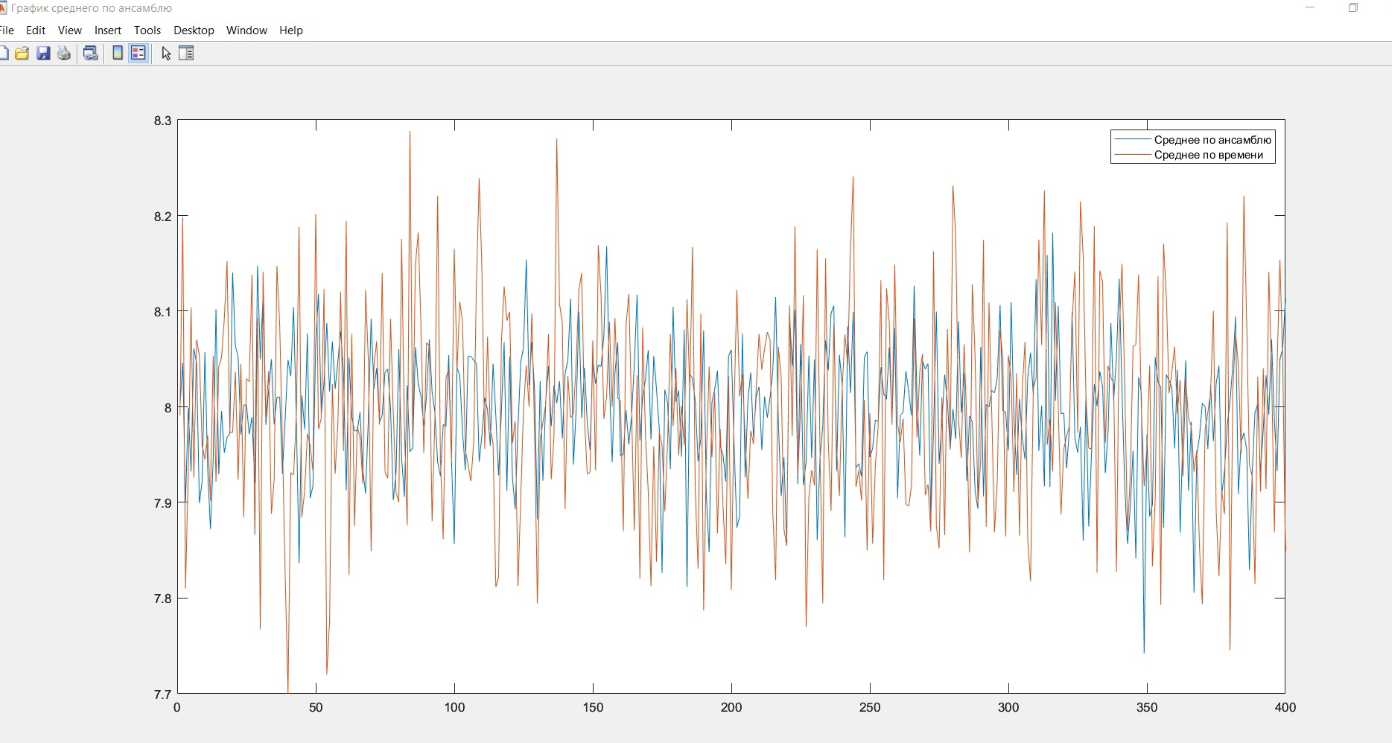
Рисунок 1 – график среднего по ансамблю и по времени

Чтобы получить настоящее среднее по ансамблю, необходимо устремить К к бесконечности, так как в работе число столбцов ограничено средние отличаются от теории.

По графику можно заметить, что процесс выглядит эргодическим по среднему: например, рассмотрим два других стационарных процесса со своими реализациями

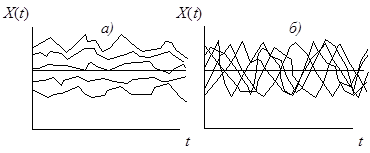
Рисунок 2 – а) неэргодический СП; б) эргодический СП

Вид графика, полученного в работе соответствует рисунку под «б» - усреднение по времени близко к усреднению по ансамблю и они сближаются с увеличением числа реализаций длин выборок.

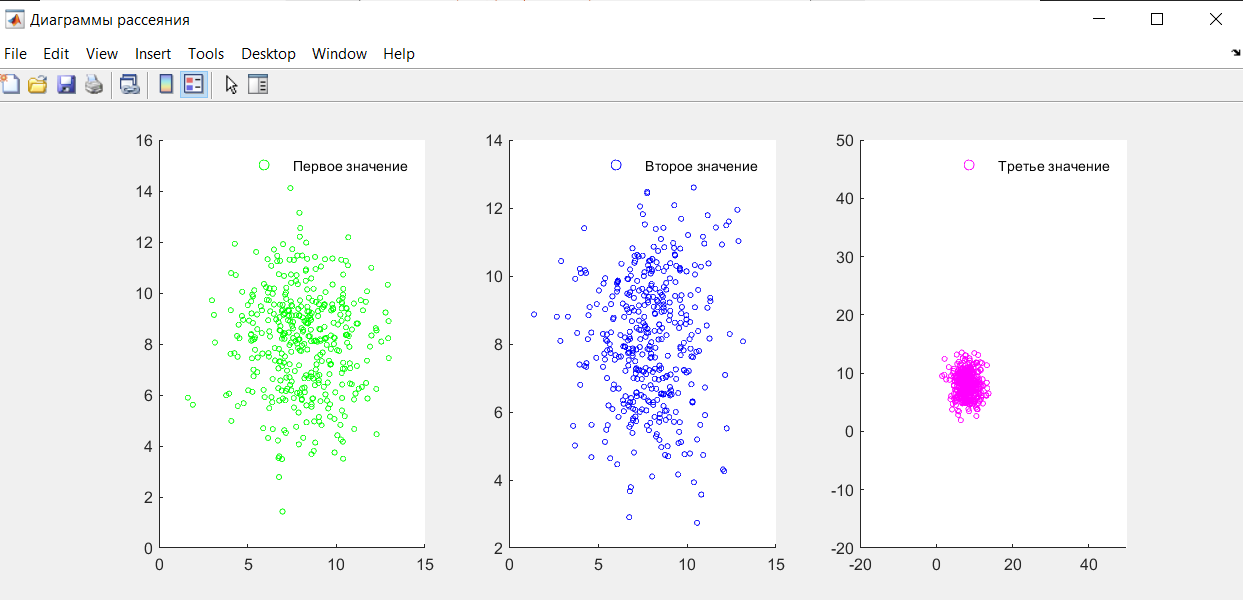
Рисунок 3 – Диаграммы рассеяния

В работе получены диаграммы рассеяния для трех разных значений n_i и n_j.

Была выполнена проверка, являются ли данные случайные процессы коррелированными, для этого проведен расчет выборочной корреляции

Наблюдается прямая связь между процессами.