Лабораторная 6
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационной безопасности
отчет
по лабораторной работе №6
по дисциплине «Алгоритмы и структуры данных»
Тема: Эвристические алгоритмы
Студенты гр. 1363 |
|
|
Афанасьев Д.К. Владимиров П.А. |
Преподаватель |
|
|
Беляев А.В. |
Санкт-Петербург
2022
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Эвристический алгоритм — это алгоритм, предназначенный для решения проблемы значительно более быстрым и эффективным способом, чем традиционные методы, за счет жертвования оптимальностью, точностью или полнотой ради скорости.
Эвристические алгоритмы часто используются для решения NP-полных задач. В этих задачах не существует известного эффективного способа быстрого и точного нахождения решения; однако, при этом если решение получено, то его можно проверить, в т.ч. в некоторых случаях оценить его расхождение от оптимального.
В зависимости от задачи эвристические алгоритмы могут быть использованы для получения итогового решения, либо же использоваться для построения некоторого базового решения, которое в дальнейшем будет улучшено другими алгоритмами оптимизации.
Пример задачи
Рассмотрим работу эвристических алгоритмов на примере NP-сложной задачи, встречающейся во многих производственных сферах: оптимальная упаковка прямоугольных объектов в двумерном пространстве. Задача поиска оптимального решения является вычислительно крайне сложной, поэтому на
практике применяются различные эвристические алгоритмы.
Next-Fit Decreasing Height
Алгоритм пытается разместить объект в самый верхний ряд (в данном алгоритме он считается единственным доступным для заполнения). Когда очередной объект не удается разместить в этом ряду (из-за своей ширины), ряд считается закрытым и открывается новый ряд, высотой равный добавляемому объекту, который становится самым левым в нем.
First-Fit Decreasing Height
В отличие от предыдущего алгоритма все ряды считаются доступными для дополнения новыми объектами. Алгоритм пытается разместить очередной объект в первый снизу ряд, в котором объекту окажется достаточно места по ширине. Только если ни одного такого ряда не найдено, объект создает новый ряд.
Best-Fit Decreasing Height
Аналогично предыдущему алгоритму все ряды считаются доступными для дополнения новыми объектами. Алгоритм пытается разместить очередной объект в ряд, в котором объекту окажется достаточно места по ширине; при этом если таких рядов несколько, то будет выбран ряд, наиболее заполненный по ширине на текущий момент.
Почти каждый из эвристических алгоритмов имеет свои преимущества и недостатки, и выбор конкретного алгоритма существенно зависит от статистических характеристик объектов, а также от желаемого отношения «скорость/качество» поиска решения.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Алгоритм NFDN
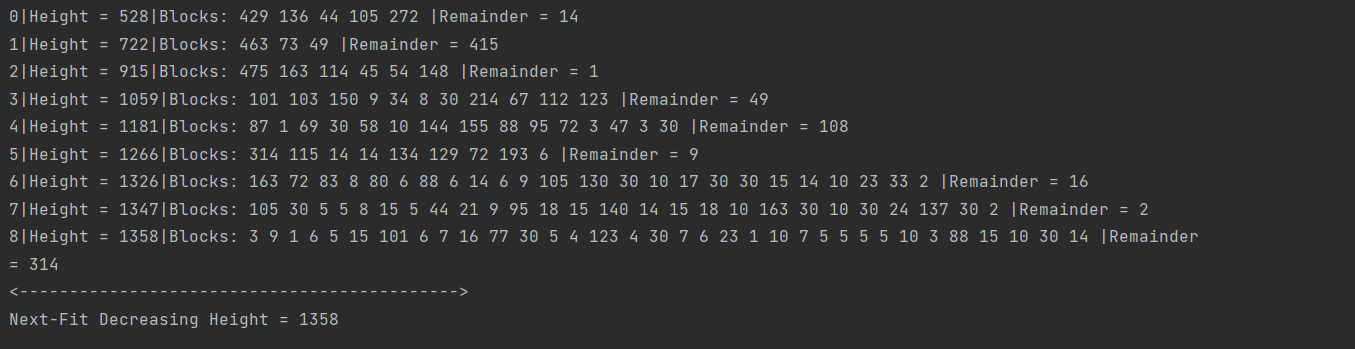
Рисунок 1 - Полный вывод программы для алгоритма NFDH
На рисунке 1 продемонстрирован полный вывод программы для алгоритма NFDH. Первое значение – порядковый номер, второе – текущая высота, дальнейшие значения – список объектов, входящих в данный ряд (их ширина), затем значение незаполненной ширины.
А
 лгоритм
FFDN
лгоритм
FFDN
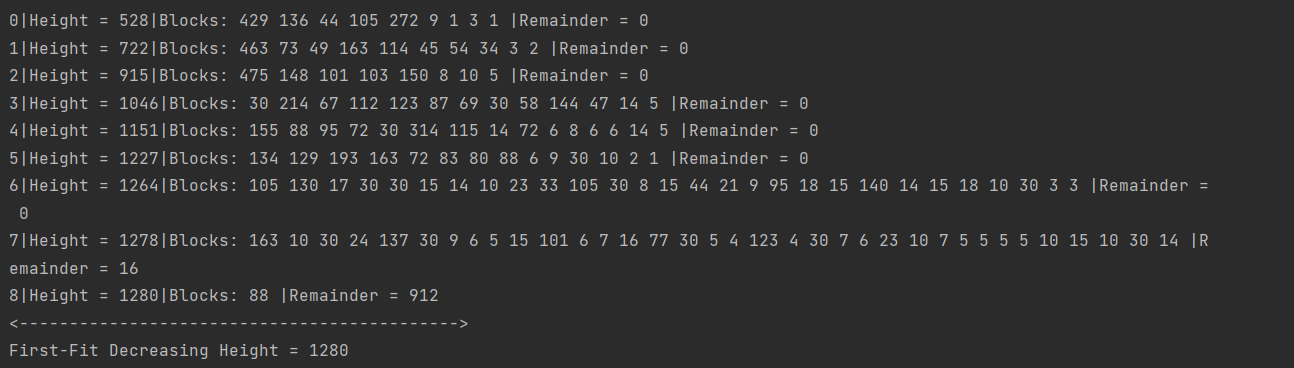
Рисунок 2 - Полный вывод программы для алгоритма FFDH
На рисунке 2 продемонстрирован полный вывод программы для алгоритма FFDH. Первое значение – порядковый номер, второе – текущая высота, дальнейшие значения – список объектов, входящих в данный ряд (их ширина), затем значение незаполненной ширины.
ИСХОДНЫЙ КОД ПРОГРАММЫ
#include <iostream>
#include <fstream>
#include <vector>
#include <algorithm>
using namespace std;
struct block {
int width;
int height;
};
struct L {
int width;
int height;
vector<int> array_of_bloks;
};
bool blocks_compare(block a, block b) {
return (a.height > b.height);
}
void show_vector(vector<block> a) {
for (vector<block>::iterator i = a.begin(); i != a.end(); i++)
cout << i->height << " " << i->width << endl;
}
void Next_Fit_Decreasing_Height(vector<block> list, int number, int backpack, int pointer, int *level, int step) {
*level += list[pointer].height;
cout << step << "|Height = " << *level << "|Blocks: ";
for (size_t i = pointer; i < number; i++) {
if (backpack - list[i].width >= 0) {
backpack -= list[i].width;
cout << list[i].width << " ";
} else {
cout << "|Remainder = " << backpack;
cout << endl;
backpack = 1000;
Next_Fit_Decreasing_Height(list, number, backpack, i, level, step + 1);
return;
}
}
cout << "|Remainder = " << backpack;
cout << "\n<-------------------------------------------->\nNext-Fit Decreasing Height = " << *level << endl << endl << endl;
}
void First_Fit_Decreasing_Height(vector<block> list, int number, vector<L> LVL, int pointer, int *level, int *max_level) {
*level += list[pointer].height;
LVL[*max_level - 1].height = *level;
bool flag;
for (size_t i = pointer; i < number; i++) {
flag = false;
for (size_t j = 0; j < *max_level; j++) {
if (LVL[j].width - list[i].width >= 0) {
LVL[j].width -= list[i].width;
LVL[j].array_of_bloks.push_back(list[i].width);
flag = true;
break;
}
}
if (!flag) {
*max_level += 1;
LVL.resize(*max_level);
LVL[*max_level - 1].width = 1000;
First_Fit_Decreasing_Height(list, number, LVL, i, level, max_level);
return;
}
}
for (size_t i = 0; i < *max_level; i++) {
cout << i << "|Height = " << LVL[i].height << "|Blocks: ";
for (size_t j = 0; j < LVL[i].array_of_bloks.size(); j++) {
cout << LVL[i].array_of_bloks[j] << " ";
}
cout << "|Remainder = " << LVL[i].width;
cout<<endl;
}
cout << "<-------------------------------------------->\nFirst-Fit Decreasing Height = " << *level << endl;
}
int main() {
ifstream file;
file.open("lab6.txt");
int number = 133, backpack = 1000, level = 0, max_level = 1;
vector<block> list_of_blocks(133);
vector<L> LVL(1);
LVL[0].width = 1000;
for (size_t i = 0; i < number; i++) {
file >> list_of_blocks[i].width;
file >> list_of_blocks[i].height;
}
sort(list_of_blocks.begin(), list_of_blocks.end(), blocks_compare);
//show_vector(list_of_blocks);
Next_Fit_Decreasing_Height(list_of_blocks, number, backpack, 0, &level, 0);
level = 0;
First_Fit_Decreasing_Height(list_of_blocks, number, LVL, 0, &level, &max_level);
return 0;
}
ВЫВОДЫ
В ходе лабораторной работы мы ознакомились с принципами работы эвристических алгоритмов при решении NP-сложных задач и реализовали алгоритмы NFDH и FFDH для предложенной задачи. По результатам работы NFDH высота рядов составила 1358 единиц, а для алгоритма FFDH – 1280, что более приближенно к оптимальному решению задачи – 1000 единиц. Исходя из этого, можно заключить, что алгоритм FFDH дает результат точнее алгоритма NFDH.
