AS_IH2_45_1363_Vladimirov
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра алгоритмической математики
отчет
по индивидуальному домашнему заданию № 2
по дисциплине «Алгебраические структуры»
Тема: Жорданова нормальная форма
Студент гр. 1363 |
|
Владимиров П.А. |
Преподаватель |
|
Абросимов И.К. |
Санкт-Петербург
2022
ВАРИАНТ ЗАДАНИЯ И ОТВЕТЫ К ЗАДАЧАМ

Рисунок 1 — Вариант задач ИДЗ
Таблица 1. Ответы к задачам
№ |
Ответ |
1 |
|
2 |
|
3 |
|
РЕШЕНИЕ ЗАДАЧ ИДЗ
Задача №1.
Привести квадратичную форму
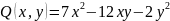 к каноническому виду ортогональным
преобразованием (в ответ записать
канонический вид и преобразование
координат).
к каноническому виду ортогональным
преобразованием (в ответ записать
канонический вид и преобразование
координат).
Решение.
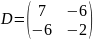 ;
;
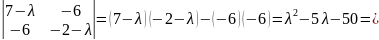
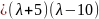 ;
;
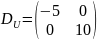 ;
;
Найдем собственные подпространства для каждого собственного числа;
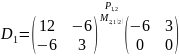 ;
;
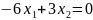 ;
;
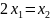 ;
;
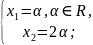
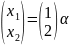 ;
;
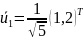 ;
;
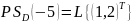 ;
;
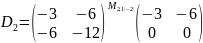 ;
;
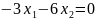 ;
;
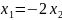 ;
;
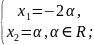
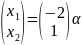 ;
;
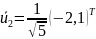 ;
;
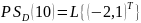 ;
;
.
Ответ: , .
Задача №2.
Найти матрицу
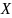 с наибольшими собственными числами,
удовлетворяющую уравнению
с наибольшими собственными числами,
удовлетворяющую уравнению
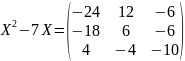 .
.
Решение.
Пусть
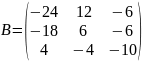 ;
;
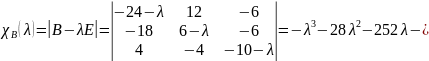
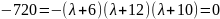 ;
;
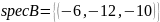 ;
;
Найдём
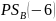 :
:
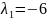 ;
;
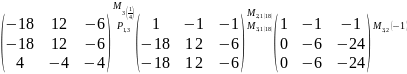
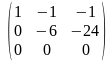 ;
;
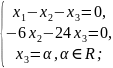
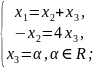
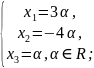
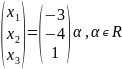 ;
;
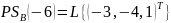 ;
;
Найдём
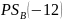 :
:
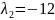 ;
;
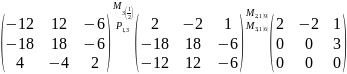 ;
;
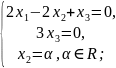
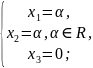
 ;
;
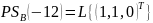 ;
;
Найдём
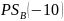 :
:
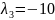 ;
;
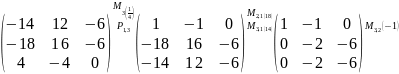
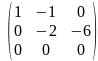 ;
;
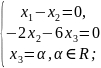
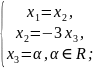
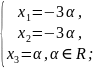
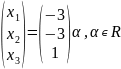 ;
;
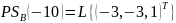 ;
;
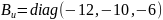 ;
;
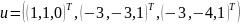 ;
;
 ;
;
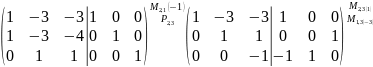
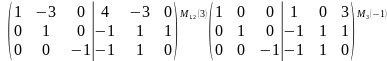
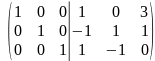 ;
;
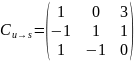 ;
;
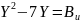 ;
;
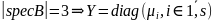 ;
;
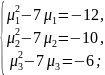
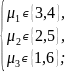
С учётом условия
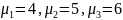 ;
;
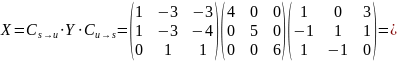
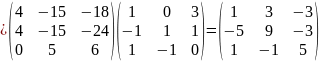 .
.
Ответ: .
Задача №3.
Найти жорданову форму и жорданов базис
матрицы
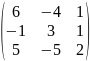 .
.
Решение.
Пусть
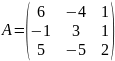 ;
;
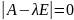 ;
;
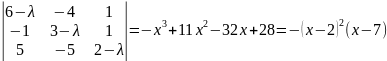 ;
;
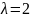 ;
;
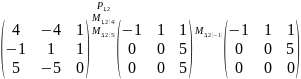 ;
;
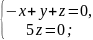
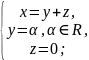
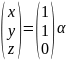 ;
;
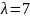 ;
;
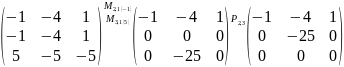 ;
;
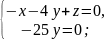
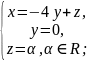
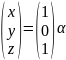 ;
;
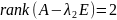 ;
;
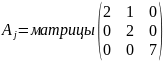 с точностью до блока;
с точностью до блока;
Перейдем к нахождению жорданового базиса;
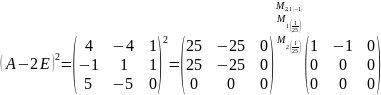 ;
;
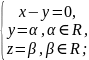
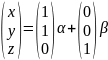 ,
,
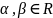 ;
;
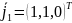 ;
;
Пусть
 и
и
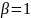 в присоединенном векторе;
в присоединенном векторе;
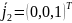 ;
;
Проверим по формуле
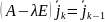 ;
;
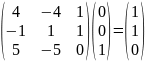 ,
значит подходит;
,
значит подходит;
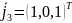 .
.
Ответ: , .

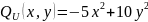 ,
,
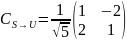 .
.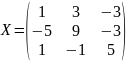 .
.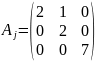 ,
,
 .
.