Добавил:

ohpetya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Алгебра и геометрия

Файл:

AS_IH1_45_1363_Vladimirov

.pdf

Скачиваний:

Добавлен:

17.03.2023

Размер:

575.03 Кб

Скачать

☆

МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра алгоритмической математики

ОТЧЕТ по индивидуальному домашнему заданию № 1

по дисциплине «Алгебраические структуры»

ТЕМА: БИЕКТИВНЫЕ ОТОБРАЖЕНИЯ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ

Студент гр. 1363			Владимиров П.А.
Преподаватель			Абросимов И.К.
Преподаватель			Абросимов И.К.

Санкт-Петербург

2022

ВАРИАНТ ЗАДАНИЯ И ОТВЕТЫ К ЗАДАЧАМ

Рисунок 1 — Вариант задач ИДЗ

															Таблица 1. Ответы к задачам

№		Ответ

1						̅̅̅̅		̅̅̅̅					̅̅̅̅	̅̅̅̅	̅̅̅̅ ̅̅̅̅
1		(1,9; 1,8), (1,9; 1,8),													(1,9; 1,8).

2					= −		4	,	=		33	.
2					= −			,	=			.
						7				7
						7				7

3		= (1				6		2)(4		7			9 8	5)(3)(10), = 15.

4		= (1				2		3	9	5			4)(6	10	8)(7), = 6.

5		̃2			̃2
				−		= 1.
			3	−	1	= 1.
	2				1
	2

6		Однополостный гиперболоид.

							РЕШЕНИЕ ЗАДАЧ ИДЗ
								Задача №1.
	Является			ли	функция			: {1, . . . ,9} → {1, . . . ,8}		заданная таблицей =
(1	2	3	4	5	6	7	8	9) инъективной? сюръективной? биективной?
8	1	2	3	6	2	7	4	5
	Решение.
							̅̅̅̅	̅̅̅̅	̅̅̅̅
	( ) = {1, . . . , 9} = 1,9 (1,9; 1,8);
	{	(3) = (6) = 2						̅̅̅̅ ̅̅̅̅
	{		3 ≠ 6				(1,9; 1,8);
			3 ≠ 6
								̅̅̅̅	̅̅̅̅	̅̅̅̅
	( ) = {8,1,2,3,6,2,7,4,5} = 1,8 (1,9; 1,8);
			̅̅̅̅ ̅̅̅̅					̅̅̅̅ ̅̅̅̅
	(1,9; 1,8) (1,9; 1,8).
					̅̅̅̅		̅̅̅̅	̅̅̅̅ ̅̅̅̅		̅̅̅̅ ̅̅̅̅
	Ответ: (1,9; 1,8), (1,9; 1,8),								(1,9; 1,8).

Задача №2.

Функция : ( ; +∞) → ( ; +∞) задана формулой ( ) = 7 2 + 8 + 7.

Найдите наименьшее и , при которых функция биективна?

Решение.

( ) = 7 2 + 8 + 7 — уравнение параболы с ветвями, направленными вверх. Найдем вершину параболы.

0 = 2∙7−8 = − 47;

	4	2		4		33
0 = 7 ∙ (−		)	+ 8 ∙ (−		) + 7 =		;
	7					7
				7

[33 ; +∞) , < 33 ,( ) = [ 7 7 ( ; +∞), ≥ 337 ;

= MIN{ | ( ) = ( ; +∞)} = 337 ;

(́ ) = 14 + 8;( ) ↓ (−∞; − 47) , ( ) ↑ (− 47 ; +∞);

((− 47 , ∞) , (337 , ∞)).

Ответ: = − 47 , = 337 .

Задача №3.
Записать перестановку (1	2	3	4	5	6	7	8	9	10) в виде
6	1	3	7	4	2	9	5	8	10

произведения независимых циклов и найти ее порядок. Решение.

Пусть = (1	2	3	4	5	6	7	8	9	10);
6	1	3	7	4	2	9	5	8	10

1(1) = 6;

2(1) = ( (1)) = 2;

(1) = (1,6,2);1(4) = 7;

2(4) = ( (4)) = 9;

3(4) = ( 2(4)) = 8;

4(4) = ( 3(4)) = 5;

(4) = (4,7,9,8,5);1(3) = 3;

(3) = (3);1(10) = 10;

(10) = (10);

Найдем порядок перестановки;

= (3,5) = 15.

Ответ: (1 6 2)(4 7 9 8 5)(3)(10), = 15.

	Задача №4.
Записать перестановку (1	2	3	4	5	6	7	8	9	10) в виде
2	3	9	1	4	10	7	6	5	8

произведения независимых циклов и найти ее порядок. Решение.

Пусть = (1	2	3	4	5	6	7	8	9	10);
2	3	9	1	4	10	7	6	5	8

1(1) = 2;

2(1) = ( (1)) = 3;

3(1) = ( 2(1)) = 9;

4(1) = ( 3(1)) = 5;

5(1) = ( 4(1)) = 4;

(1) = (1, ,2,3,9,5,4);

1(6) = 10;

2(6) = ( (6)) = 8;

(6) = (6,10,8);1(7) = 7;

(7) = (7);

Найдем порядок перестановки;

= (6,3) = 6.

Ответ: (1 2 3 9 5 4)(6 10 8)(7), = 6.

Задача №5.

Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов в исходной системе координат и построить эскиз графика: 3 2 − 5 2 + 6 − 6 + 42 = 75.

Решение.

Уравнение имеет вид 11 2 + 2 12 + 2 13 + 22 2 + 2 23 + + 33 = 0;

Найдем коэффициенты;

11	= 3, 12 = 3, 13									= −3, 22 = −5, 23			= 21, 33 = −75;
			11	12			\| = \|	3		3	\| = −24;
∆= \|							\| = \|	3		−5	\| = −24;
			12		22			3		−5
∆≠ 0, значит найдем центр канонической системы координат;
{ 11 0 + 12 0 + 13 = 0,
		+				+				= 0;
12			0	22			0	23
3 0 + 3 0 − 3 = 0,
{3			− 5 + 21 = 0;
0				0
{ 0 = −2,
			= 3;
0
Мы перешли к уравнению в системе координат ′ ′ ′;
′	+			′2 + 2					′ ′ + ′2			= 0, где ′		=		+		+ ;
33			11				12				22		33	13	0	23	0	33
′	= −3 + 21 − 75 = −6;
33				0				0

Уравнение превратится в 3 ′2 + 6 ′ ′ − 5 ′2 − 6 = 0;

Делаем поворот системы на угол ;

′ = ̃ cos( ) − ̃ sin( ), { ′ = ̃ sin( ) + ̃ cos( );

cot(2 ) = 11− 22;

2 12

cot(2 ) = 43;

acot(4)

= 3 ;

sin(2 ) = 35; cos(2 ) = 45;

cos( ) = √cos(22 ) + 12;

sin( ) = √1 − cos2( );

cos( ) = 3√1010;

sin( ) = √1010;

Подставляем коэффициенты;

′ =

3√

−

√

{

√10 ̃

3√10 ̃

′ =

;

3√

Уравнение превратится в −5 (

√

+ 6 (

√

−

)

) (

3√

√

−

) + 3

(

−

)

− 6 = 0;

4̃2 − 6 ̃2 − 6 = 0;

̃2

−

= 1;

Данное уравнение является гиперболой;

Центр канонической системы координат в точке (−2,3).

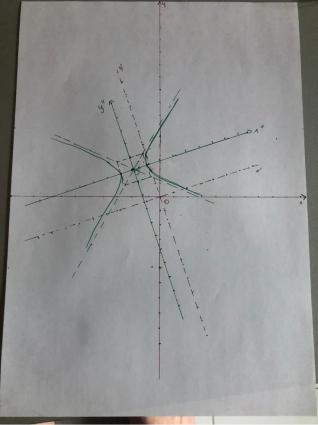
Рисунок 2 — Эскиз графика

	̃2			̃2
Ответ:			−		= 1.
		3		1
	2

Задача №6.

Определить тип поверхности второго порядка и найти координаты ее центра (если он существует): 5 2 + 2 + 2 + 6 − 6 − 6 − 2 + 2 + +2 = 0.

Решение.

Определим тип поверхности второго порядка по инвариантам; Сравним заданное уравнение с общим уравнением поверхности второго

порядка;

11 2 + 22 2 + 33 2 + 2 12 + 2 13 + 2 23 + 2 1 + 2 2 + +2 3 + 0 = 0;

Найдем коэффициенты;

11 = 5, 22 = 1, 33 = 1, 12 = 3, 13 = −3, 23 = −3, 1 = −1,2 = 1, 3 = 1, 0 = 0;

Вычислим ортогональные инварианты 1, 2, , ∆;

1 = 11 + 22 + 33 = 5 + 1 + 1 = 7;

	2	11	12		\| + \|	11		13		22		23		5	3	\| + \|	5
	2	= \|	22		\| + \|	13		33	\| + \|			33	\| = \|		1	\| + \|	−3
		12	22			13		33		23		33		3	1		−3
+ \|	1	−3\| = −16;
	−3	1
		11	12		13			5		3	−3
	= \| 12		22		23\| = \| 3					1 −3\| = −4;
		13	23		33			−3		−3	1
		11	12		13		1			5	3	−3		−1
		12	22		23		2			3	1	−3		1
	∆= \|			23				\| = \|		−3	−3	1		1	\| = 4;
		13		23	33		3			−3	−3	1		1
		1	2		3		0			−1 1		1		0
	Уравнение задает						однополостный					гиперболоид,					так

2 < 0 и ∆> 0.

Ответ: однополостный гиперболоид.

−31 | +

как ≠ 0,

Соседние файлы в предмете Алгебра и геометрия

#
17.03.2023111.2 Кб1AaG IH1 35 1363 Vladimirov.docx
#
17.03.2023499.24 Кб0AaG IH2 35 1363 Vladimirov.pdf
#
17.03.2023560.69 Кб0AaG IH3 35 1363 Vladimirov.pdf
#
17.03.2023575.03 Кб7AS_IH1_45_1363_Vladimirov.pdf
#
17.03.202378.84 Кб7AS_IH2_45_1363_Vladimirov.docx