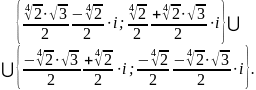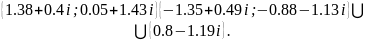
AaG IH1 35 1363 Vladimirov
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра алгоритмической математики
отчет
по индивидуальному домашнему заданию № 1
по дисциплине «Алгебра и геометрия»
Тема: многочлены и комплексные числа
Студент__ гр. 1363 |
|
Владимиров П.А. |
Преподаватель |
|
Абросимов И.К. |
Санкт-Петербург
2021

Рисунок 1 – Вариант задач ИДЗ
Таблица №1. Ответы к задачам
№ |
Ответ |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
Формула
соответствует окружности с центром
в точке O |
7 |
Не смог построить эллипс. |
8 |
|
9 |
|
РЕШЕНИЕ ЗАДАЧ ИДЗ
Задача №1.
Вычислить
в алгебраической форме:
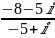 .
.
Дано:
.
Решение:
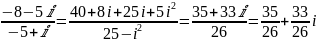 .
.
Ответ: .
Задача №2.
Вычислить:
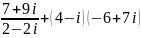 .
.
Дано:
.
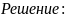
Расставим порядок действий: деление, умножение, сложение:
1)
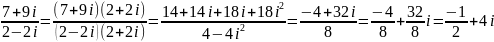 ;
;
2)
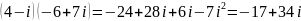 ;
;
3)
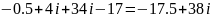 .
.
Ответ: .
Задача №3.
Решить уравнение:
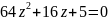 .
.
Дано:
.
Решение:
Найдем дискриминант:
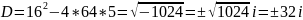 ;
;
Найдем корни:
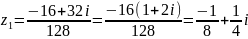 ,
,
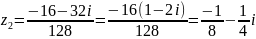 .
.
Ответ: .
Задача №4.
Решить
уравнение:
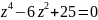 .
.
Дано:
.
Решение:
;
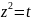 ;
;
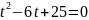 ;
;
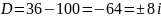 ;
;
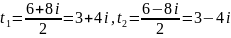 ;
;
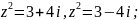
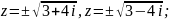
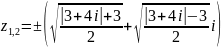 ;
;
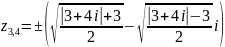 ;
;
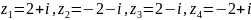 .
.
Ответ: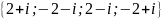 .
.
Задача №5.
Решить
в алгебраической форме:
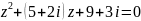 .
.
Дано:
.
Решение:
;
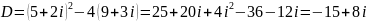 ;
;
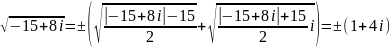 ;
;
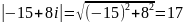 ;
;
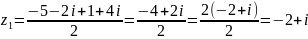 ;
;
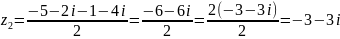 .
.
Ответ:
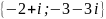 .
.
Задача №6.
Построить
на комплексной плоскости множество
точек, удовлетворяющих неравенству:
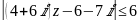 .
.
Дано:
.
Решение:
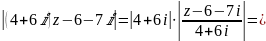
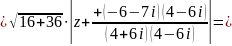
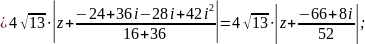
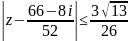 ;
;
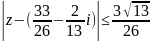 .
.
Ответ: Формула соответствует окружности с центром в точке O и радиусом . Границы и внутренняя часть окружности включены, так как неравенство нестрогое.
Задача №7.
Построить
множество точек на комплексной плоскости,
удовлетворяющих неравенству
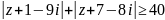 .
.
Дано:
.
Решение:
;
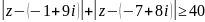 ;
;
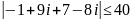 ;
;
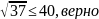 .
.
Ответ: не смог построить эллипс.
Задача №8.
Решить
уравнение:
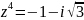 (ответ в алгебраической форме без
тригонометрических функций).
(ответ в алгебраической форме без
тригонометрических функций).
Дано:
.
Решение:
;
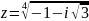 ;
;
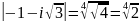 ;
;
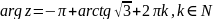 ;
;
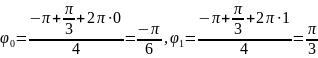 ;
;
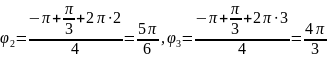 ;
;
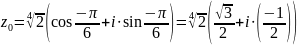 ;
;
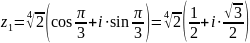 ;
;
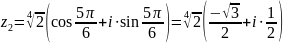 ;
;
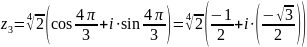 ;
;
Ответ: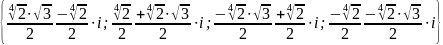 .
.
Задача №9.
Решить
уравнение:
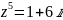 (ответы представить в алгебраической
форме с точностью до сотых).
(ответы представить в алгебраической
форме с точностью до сотых).
Дано:
.
Решение:
;
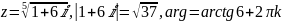 ;
;
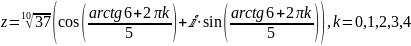 ;
;
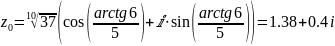 ;
;
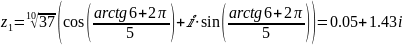 ;
;
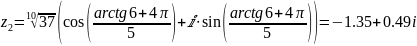 ;
;
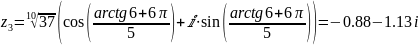 ;
;
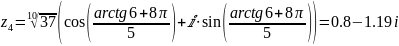 .
.
Ответ:
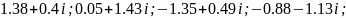
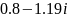 .
.

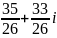 .
.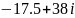 .
.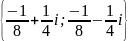 .
.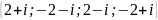 .
.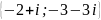 .
.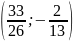 и радиусом
и радиусом
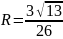 .
Границы и внутренняя часть окружности
включены, так как неравенство нестрогое.
.
Границы и внутренняя часть окружности
включены, так как неравенство нестрогое.