Лабы / lab2

Цель работы.

Преобразовать исходную систему уравнений в СНЛАУ, описывающую статические режимы, рассчитать статические характеристики динамической системы с помощью языка Matlab.

Вариант лабораторной работы.

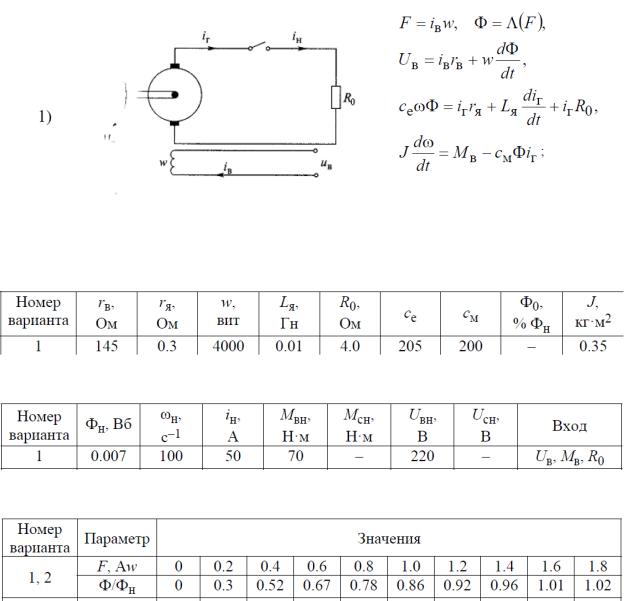
В варианте №1 используется ГПТ НВ, работающий на активную нагрузку. Его параметры приведены ниже.

Рис. 1. ГПТ НВ, работающий на активную нагрузку

Таблица 1. Параметры объекта моделирования.

Таблица 2. Входные, выходные и нормировочные переменные.

Таблица 3. Кривые намагничивания.

Постановка задачи.

Статический режим динамической системы – это ее равновесное состояние, соответствующее окончанию переходных процессов. Например, изменение напряжения возбуждения на новое постоянное значение вызывает изменение МДС, магнитного потока, тока и напряжения генератора и т.д. Переходный процесс заканчивается новыми установившимися значениями

2

этих величин, т.е. новым статическим режимом. Статический режим будет описывать система алгебраических уравнений, т.е. уравнений, куда не входят производные, так как последние в статическом режиме равны нулю.

Все статические режимы могут быть описаны СНЛАУ, записанной в обобщенной форме относительно компонент векторов и и х:

Математическая модель ГПТ НВ, работающего на активную нагрузку.

1.Запишем исходную систему уравнений, описывающую наш ГПТ НВ.

= в, Φ = Λ( )

Φв = в в +

3 0

Выразим ток нагрузки через ток якоря: н = г − в

3

Выражаем ток возбуждения через полином, найденный в лабораторной

работе №1: в = (Φ), н = г − (Φ).

В исходной системе уравнений выразим производные по переменным состояния и подставим выражения для тока нагрузки и тока возбуждения:

Приравниваем производные к нулю:

(Φ)

в − в = 0

{ Φ − г я − г 0 = 0в − мΦг = 0

Преобразуем систему уравнений:

в − (Φ) в = 0 { Φ − г я − г 0 = 0в − мΦг = 0

в − мΦг = 0

Перепишем данную систему через отнормированные параметры:

̅̅

{в в − Фн гнФ г̅= 0.

4

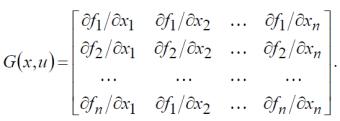
Запишем систему через переменные состояния, полученные выше: =

Переписываем нашу систему уравнений:

11 1 − ̅( 1) = 0, {21 1 3 − 22 2 − 23 2 3 = 0,

31 2 − 32 1 2 = 0,

В данном случае наша система решается методом Ньютона. Для этого нам нужна следующая матрица:

Программа для решения уравнения методом Ньютона представлена в листинге 1.

5

Листинг 1. Основная программа.

clear clc rv=145;

r_ancor=0.3; vv=4000; L_ancor=0.01; R0=4; Ce=205; Cm=200; J=0.35;

Field_n=0.007; omega=100; i_n=50; Mvn=70; Uvn=220; iv=Uvn/rv;

global a11 a21 a22 a23 a31 a32 pF a11=Uvn*vv/(rv*iv*vv); a21=Ce*omega*Field_n; a22=i_n*r_ancor;

a23=i_n*R0; a31=Mvn; a32=Cm*Field_n*i_n;

pF=[0.7479 0 -0.1896 0 0.5022 0];

length=length(1.2:-0.01:0.05);

u_1=[1.2:-0.01:0.05; ones(1,length); ones(1,length)]; x0=[1, 1, 1]';

for i=1:length

Fun(i,:)=newton('Fun_F','Fun_G', x0, u_1(:,i), 0.0001); x0=Fun(i,:)';

end

figure

subplot(2,2,1) plot(u_1(1,:),Fun(:,1)) grid minor xlabel('u_в') ylabel('Ф')

ylim([0.9*min(Fun(:,1)) 1.1*max(Fun(:,1))])

subplot(2,2,2) plot(u_1(1,:),Fun(:,2)) grid minor xlabel('u_в') ylabel('i')

ylim([0.9*min(Fun(:,2)) 1.1*max(Fun(:,2))])

subplot(2,2,3) plot(u_1(1,:),Fun(:,3)) grid minor xlabel('u_в') ylabel('\omega')

ylim([0.9*min(Fun(:,3)) 1.1*max(Fun(:,3))])

subplot(2,2,4) plot(u_1(1,:),Fun(:,1),u_1(1,:),Fun(:,2),u_1(1,:),Fun(:,3))

6

grid minor xlabel('u') ylabel('x')

legend('Ф','i','\omega','location','best') ylim([0 20])

u_1=[ones(1,length); 1.2:-0.01:0.05 ; ones(1,length)]; x0=[1, 1, 1]';

for i=1:length

Fun(i,:)=newton('Fun_F','Fun_G', x0, u_1(:,i), 0.0001); x0=Fun(i,:)';

end

figure

subplot(2,2,1) plot(u_1(2,:),Fun(:,1)) grid minor xlabel('M_в') ylabel('Ф')

ylim([0.9*min(Fun(:,1)) 1.1*max(Fun(:,1))])

subplot(2,2,2) plot(u_1(2,:),Fun(:,2)) grid minor xlabel('M_в') ylabel('i')

ylim([0.9*min(Fun(:,2)) 1.1*max(Fun(:,2))])

subplot(2,2,3) plot(u_1(2,:),Fun(:,3)) grid minor xlabel('M_в') ylabel('\omega')

ylim([0.9*min(Fun(:,3)) 1.1*max(Fun(:,3))])

subplot(2,2,4) plot(u_1(2,:),Fun(:,1),u_1(2,:),Fun(:,2),u_1(2,:),Fun(:,3)) grid minor

xlabel('u') ylabel('x')

legend('Ф','i','\omega','location','best')

u_1=[ones(1,length); ones(1,length); 1.2:-0.01:0.05 ]; x0=[1, 1, 1]';

for i=1:length

Fun(i,:)=newton('Fun_F','Fun_G', x0, u_1(:,i), 0.0001); x0=Fun(i,:)';

end

figure subplot(2,2,1)

plot(u_1(3,:),Fun(:,1)) grid minor xlabel('R_0') ylabel('Ф')

ylim([0.9*min(Fun(:,1)) 1.1*max(Fun(:,1))])

subplot(2,2,2) plot(u_1(3,:),Fun(:,2))

7

grid minor xlabel('R_0') ylabel('i')

ylim([0.9*min(Fun(:,2)) 1.1*max(Fun(:,2))])

subplot(2,2,3) plot(u_1(3,:),Fun(:,3)) grid minor xlabel('R_0') ylabel('\omega')

ylim([0.9*min(Fun(:,3)) 1.1*max(Fun(:,3))])

subplot(2,2,4) plot(u_1(3,:),Fun(:,1),u_1(3,:),Fun(:,2),u_1(3,:),Fun(:,3)) grid minor

xlabel('u') ylabel('x')

legend('Ф','i','\omega','location','best')

Листинг 2. Функция, реализующая метод Ньютона.

function [x] = newton(F, G, x0, u, e) y=feval(F, x0, u);

x=x0; while(norm(y)>e)

gr=feval(G, x, u); x=x-inv(gr)*y; y=feval(F, x, u); clc

end

Листинг 3. Функция, вычисляющая матрицу частных производных.

function G = Fun_G( x, u)

global a11 a21 a22 a23 a31 a32 pF G1=[-polyval(polyder(pF), x(1)) 0 0]; G2=[a21*x(3) -a22-a23*u(3) a21*x(1)]; G3=[-a32*x(2) -a32*x(1) 0];

G=[G1; G2; G3]; end

Листинг 4. Функция, вычисляющая значения уравнений системы.

function f= Fun_F(x, u)

global a11 a21 a22 a23 a31 a32 pF f1=a11*u(1)-polyval(pF, x(1)); f2=a21*x(1)*x(3)-a22*x(2)-a23*x(2)*u(3); f3=a31*u(2)-a32*x(1)*x(2);

f=[f1; f2; f3]; end

Статические характеристики системы представлены на рис. 1-3.

8

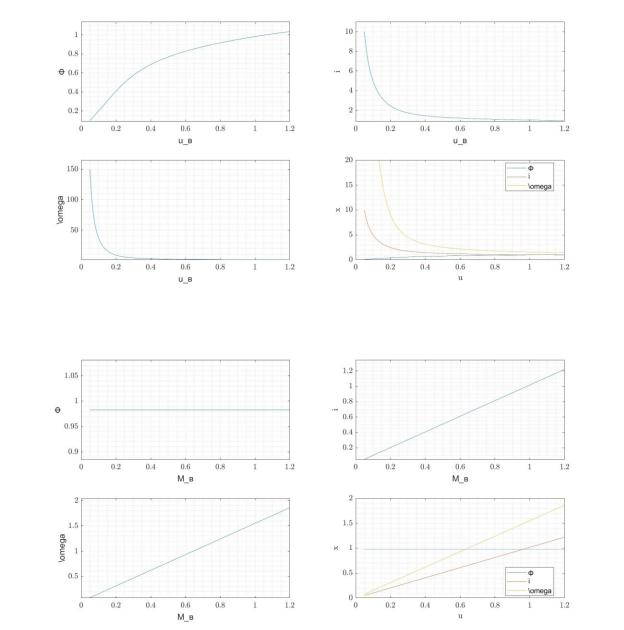
Рис. 1. Статические характеристики при изменении параметра u1 (0.05, 1.2)

Рис. 2. Статические характеристики при изменении параметра u2 (0.05, 1.2)

9

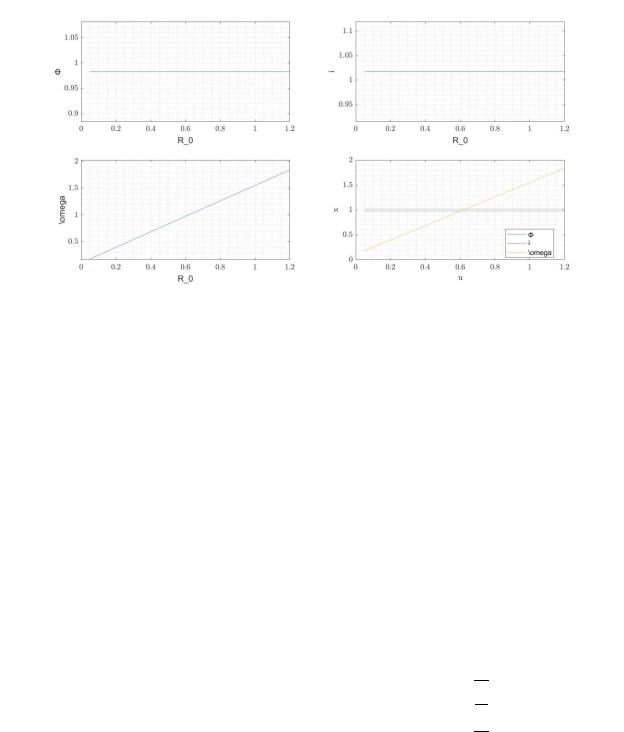
Рис. 3. Статические характеристики при изменении параметра u3 (0.05, 1.2)

Выводы.

В ходе выполнения данной лабораторной работы использовалась система уравнений СНЛАУ, описывающая статические режимы:

1( , ) = 11 1 − ̅( 1) = 0, { 2( , ) = 21 1 3 − 22 2 − 23 2 3 = 0,

3( , ) = 31 2 − 32 1 2 = 0,

В качестве функции обратной кривой намагничивания использовался нормированный полином 5-й степени, найденный в предыдущей работе:

̅( ) = 0.7479 5 − 0.1896 3 + 0.5022 .

Также с помощью Matlab были рассчитаны и построены статические характеристики нашей системы, кроме того, были найдены значения

1 Φ 0,983

переменных состояния в установившемся режиме: [ 2] = [ г] = [1,017].

3 1,55

10