Лабы / lab1

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В. И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра КСУ

ОТЧЕТ

по лабораторной работе №1

по дисциплине «Моделирование систем управления»

Тема: аппроксимация обратной кривой намагничивания электрической машины на основе метода наименьших квадратов

Вариант 1

Студент гр. 9491 Горобец А. А.

Преподаватель Лукомская О. Ю.

Санкт-Петербург

2023

Цель работы.

Аппроксимировать нелинейную зависимость F(Ф), заданную таблично, в промежуточных точках; аппроксимирующую функцию найти в виде полинома заданной степени; оценить зависимость точности аппроксимации от степени полинома.

Постановка задачи.

1. Исходные данные.

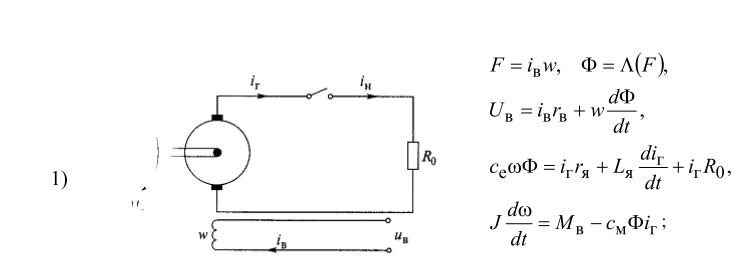
Рис. 1. Математическая модель ГПТ НВ.

1. Параметры объекта моделирования.

2. Входные, выходные и нормировочные переменные.

3. Кривые намагничивания.

Расчет базисных величин.

В таблице 3 уже приведены отнормированные значения потока. Для нахождения номинальной МДС воспользуемся следующей формулой:

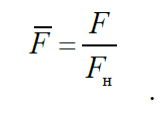
Найдем номинальное значение МДС. Для этого возьмем схему замещения в установившемся режиме. Она представлена на рис. 2.

Расчет коэффициентов нормирующего полинома.

Листинг 1. Код программы на языке Matlab.

clear all

F=(0:0.2:1.8).*4000;

Fild_norm=[0 0.3 0.52 0.67 0.78 0.86 0.92 0.96 1.01 1.02];

Fild_n=0.007;

Fild=Fild_norm.*Fild_n;

F_norm=F./(4000*220/145);

j=1;

for i=1:2:5;

G_norm5(j,:)=Fild_norm.^i;

G5(j,:)=Fild.^i;

j=j+1;

end

G_norm5=G_norm5';

G5=G5';

j=1;

for i=1:2:3;

G_norm3(j,:)=Fild_norm.^i;

G3(j,:)=Fild.^i;

j=j+1;

end

G_norm3=G_norm3';

G3=G3';

C_norm5=inv(G_norm5'*G_norm5)*(G_norm5'*F_norm');

C_norm3=inv(G_norm3'*G_norm3)*(G_norm3'*F_norm');

C5=inv(G5'*G5)*(G5'*F');

C3=inv(G3'*G3)*(G3'*F');

Flongnorm=0:0.01:max(Fild_norm);

Flong=0:0.0001:max(Fild);

p_norm5=polyval([C_norm5(3) 0 C_norm5(2) 0 C_norm5(1) 0],Flongnorm);

p_norm3=polyval([C_norm3(2) 0 C_norm3(1) 0],Flongnorm);

p5=polyval([C5(3) 0 C5(2) 0 C5(1) 0],Flong);

p3=polyval([C3(2) 0 C3(1) 0],Flong);

I_norm5=sum((F_norm-polyval([C_norm5(3) 0 C_norm5(2) 0 C_norm5(1) 0],Fild_norm)).^2);

I_norm3=sum((F_norm-polyval([C_norm3(2) 0 C_norm3(1) 0],Fild_norm)).^2);

I5=sum((F-polyval([C5(3) 0 C5(2) 0 C5(1) 0],Fild)).^2);

I3=sum((F-polyval([C3(2) 0 C3(1) 0],Fild)).^2);

subplot(2,2,1)

hold on

text(max(Fild)/3, max(F)/2, strcat('I = ',num2str(I3)))

plot(Fild,F,'*');

plot(Flong,p3)

plot(Flong,polyval(polyfit(Fild,F,3),Flong));

grid minor

xlabel('Ф')

ylabel('F')

title('Ненормированный полином 3-й степени')

legend('Опытные данные','Апроксимация методом наименьших квадратов','Апроксимация методом polyfit', 'location', 'best')

axis([0 max(Fild) 0 max(F)])

subplot(2,2,2)

hold on

text(max(Fild)/3, max(F)/2, strcat('I = ',num2str(I5)))

plot(Fild,F,'*');

plot(Flong,p5)

plot(Flong,polyval(polyfit(Fild,F,5),Flong));

grid minor

xlabel('Ф')

ylabel('F')

title('Ненормированный полином 5-й степени')

legend('Опытные данные','Апроксимация методом наименьших квадратов','Апроксимация polyfit', 'location', 'best')

axis([0 max(Fild) 0 max(F)])

subplot(2,2,3)

hold on

text(max(Fild_norm)/3, max(F_norm)/2, strcat('I = ',num2str(I_norm5)))

plot(Fild_norm,F_norm,'*');

plot(Flongnorm,p_norm5)

plot(Flongnorm,polyval(polyfit(Fild_norm,F_norm,5),Flongnorm));

grid minor

xlabel('Ф')

ylabel('F')

title('Нормированный полином 5-й степени')

legend('Опытные данные','Апроксимация методом наименьших квадратов','Апроксимация polyfit', 'location', 'best')

axis([0 max(Fild_norm) 0 max(F_norm)])

subplot(2,2,4)

hold on

text(max(Fild_norm)/3, max(F_norm)/2, strcat('I = ',num2str(I_norm3)))

plot(Fild_norm,F_norm,'*');

plot(Flongnorm,p_norm3)

plot(Flongnorm,polyval(polyfit(Fild_norm,F_norm,3),Flongnorm));

grid minor

xlabel('Ф')

ylabel('F')

title('Нормированный полином 3-й степени')

legend('Опытные данные','Апроксимация методом наименьших квадратов','Апроксимация polyfit', 'location', 'best')

axis([0 max(Fild_norm) 0 max(F_norm)])

Графики полиномов представлены на рис. 3.

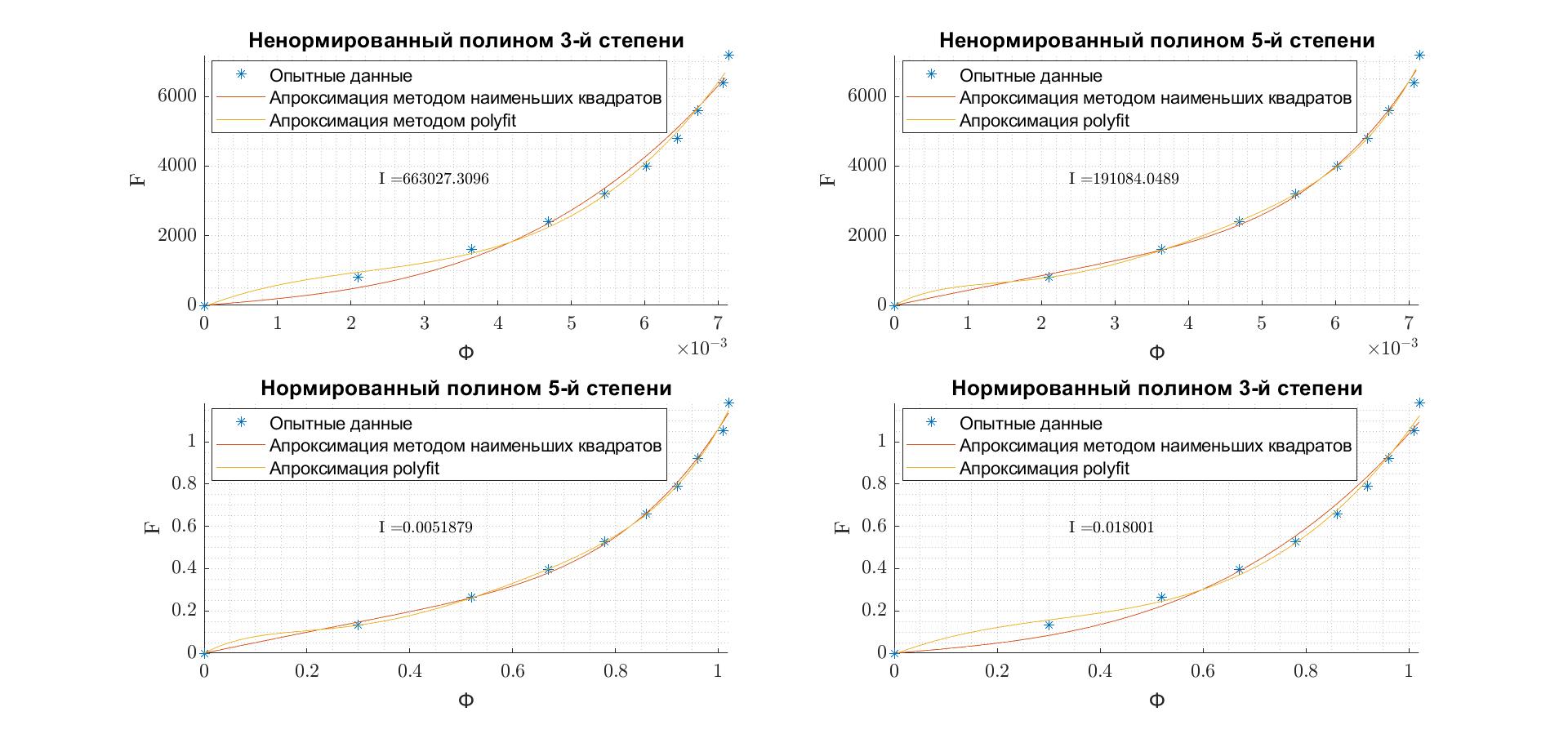
Рис. 3. Графики нормированных и ненормированных полиномов.

Нормированные полиномы (верхний – 3-я степень, нижний – 5-я степень соответственно):

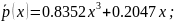
Ненормированные полиномы (верхний – 3-я степень, нижний – 5-я степень соответственно):

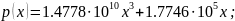
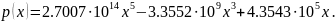
Выводы.

В ходе выполнения лабораторной работы была аппроксимирована нелинейная зависимость F(Ф), заданная таблично. Как оказалось, качество аппроксимации при степени аппроксимирующего полинома 5 лучше, чем при степени 3. Но при этом более высокая степень аппроксимирующего полинома не гарантирует лучшее качество аппроксимации.