
Task 3.
Devices with dynamic control. Klystron.
Calculate the angle of flight
in the drift space at which an electron caught in the accelerating
phase of the voltage in the 1st resonator will catch up with an
electron caught in the braking phase. The calculation should be
carried out in a kinematic approximation. When calculating, take:
constant accelerating voltage
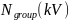 ,
gap length (interaction area)
,
gap length (interaction area)
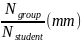 ,
depth of speed modulation
,
depth of speed modulation
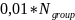 ,
operating frequency
,
operating frequency
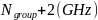 .
To solve the problem using normalized parameters: modulation depth,
span angle, grouping parameter.
.
To solve the problem using normalized parameters: modulation depth,
span angle, grouping parameter.
Analyze how the grouping
process will change when taking into account the forces of the
spatial charge, if the beam current is equal
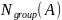 ,
and the diameter of the beam
,
and the diameter of the beam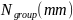 ?
At what distance from the middle of the modulating gap will the
maximum grouping be? Comment on the result.
?
At what distance from the middle of the modulating gap will the
maximum grouping be? Comment on the result.
Given:
Constant accelerating voltage:
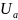 =1kV
=1kV
Gap length: L=0,071mm
Speed modulation depth: v=0,14
Operating frequency: f=3 GHz
Beam Current: I=1 A
Beam diameter: d=1 mm
Solution:
Calculation of the span angle:
The first way:
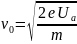
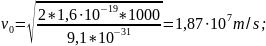
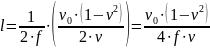
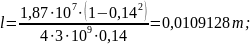
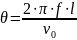
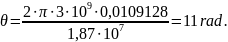
The second way:
Grouping Parameter:
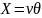
The phase difference will be
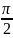 ,
so the grouping parameter will be
.
This is so because the accelerated electron has caught up with the
decelerated one.
,
so the grouping parameter will be
.
This is so because the accelerated electron has caught up with the
decelerated one.
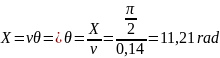
How will the grouping process change when taking into account the forces of the spatial charge?
Grouping parameter adjusted for Coulomb forces:
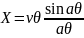
Where
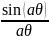 – correction, which takes into account the Coulomb interaction.
– correction, which takes into account the Coulomb interaction.
Where a–
disaggregation parameter
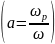 ,
where
,
where
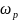 - plasma
frequency,
- plasma
frequency,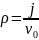 – the
density of the spatial charge of the beam,
– the
density of the spatial charge of the beam,
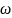 – modulation frequency
– modulation frequency
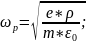
Calculation of the correction:
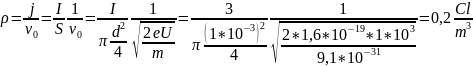
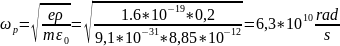
Grouping parameter without taking into account the spatial charge can be calculated by the following formula:
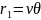
*In this case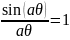 .
.
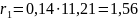
The grouping parameter with taking into account the spatial charge is determined as follows:
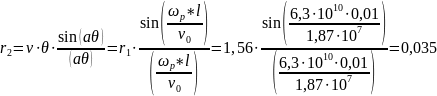
3. The distance from the middle of the modulating gap at which the maximum grouping will be
Maximum grouping, characterized by the maximum grouping parameter:
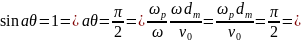
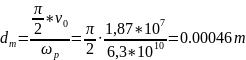
Therefore, the distance from the middle of the modulating gap is calculated by the following formula:
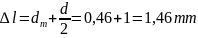
Answer.
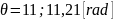
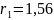 ,
,
 .
The interaction parameter is reduced due to the
.
The interaction parameter is reduced due to the
interaction forces between the electrons.
The maximum grouping parameter will be at a distance of 1,46 mm.
Sources: Григорьев А.Д., Иванов В.А., Молоковский С.И. Микроволновая электроника: Учебник. СПб.: Издательство «Лань», 2015. – 637 с.
Task 4.
Devices with dynamic control.TWT.
To calculate the parameters of the spiral retarding system (ZS) for TWT.
Initial (set) values for calculation:
Power gain
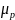 =30
dB
=30
dBThe firstance of the electron beam
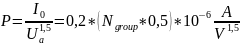 .
The radius of the electron beam
.
The radius of the electron beam
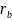 =2
mm
=2
mm
The ratio of the beam radius to the spiral radius /a=0,7
Accelerating beam voltage
The frequency is
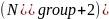 GHz.
GHz.Accelerating voltage = 1,5 kV+(
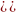 )
kV
)
kVIn the calculations, take the coupling resistance equal to
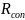 =
100 Om
=
100 Om
Determine the following values and parameters:
Current and power of the electron beam – I0, P0
Electron beam velocity

The step of the spiral CS is p, at which the conditions of synchronism of the beam and electromagnetic wave motion are met
The length of the spiral ZS, which provides the specified value of the gain
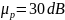
Draw and justify the typical frequency response and the Amplitude characteristic of the LBV. How these characteristics will change when the coupling resistance changes? Draw on the same graph.
Given:
Power gain
Electron beam perveance: P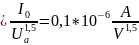
Electron beam radius =2 mm
The ratio of the beam radius to the spiral radius /a=0,7
Accelerating beam voltage
Frequency 3 GHz
Accelerating voltage: =5,7 kV
In the calculations, take the coupling resistance equal to = 100 Om
Solution:
Current and power of the electron beam
The law of degree 3/2:
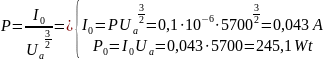
Speed of electron beam:
The law of conservation of energy:
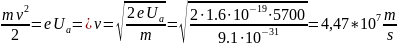
The step of the spiral CS, at which the conditions of synchronism of the beam and electromagnetic wave motion are met
Synchronism condition:
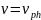
The step of the slow-wave structure:
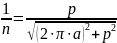
Where n - deceleration
coefficient by definition (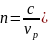 .
.
In this way:
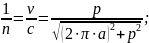
Where:
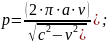
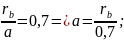
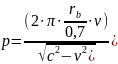
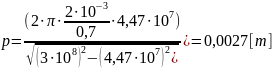
The length of the spiral ZS, which provides a set value of the gain
Gain factor:
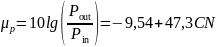 ;
;
Where:
C - gain constant:
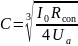
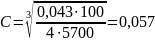
Where:
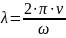
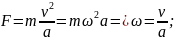
Therefore:
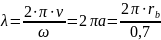
We get:
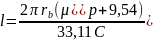
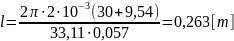
Frequency response and Amplitude characteristics of TWT:
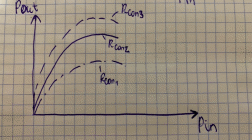
Fig 4.1. Amplitude characteristic of TWT
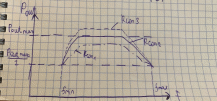
Fig 4.2. Amplitude-frequency response of TWT
The gain depends on the gain constant:
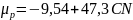
The gain constant depends on the coupling resistance:
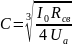
From here it can be seen that with increasing communication resistance, the gain constant increases, and increasing the gain constant increases the gain factor. Consequently, the dependencies will go higher with increasing bond resistance:
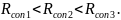
Answer:
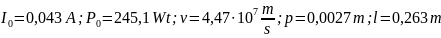
Sources: Lecture 7 MWE
Microwave electronics pdf.pdf
Task 5.
Devices with dynamic control. M-type devices.
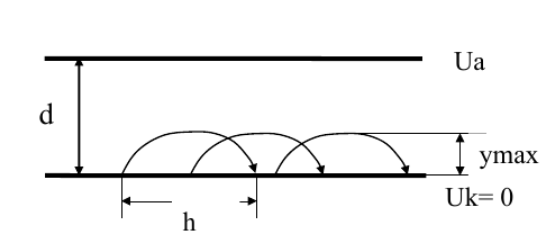
Calculate the value of the critical magnetic induction
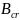 for
the
for
the
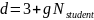 mm
value and the
potential
value from task No. 4
mm
value and the
potential
value from task No. 4
Assuming that
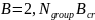 calculate the cyclotron frequency, determine the height of the
cathode electron layer ymax
calculate the cyclotron frequency, determine the height of the
cathode electron layer ymax
Calculate the step of the electronic trajectory h.
Assuming the potential distribution in the interelectrode gap to be linear, find the value of the maximum velocity in the electron cloud.
How will the frequency of magnetron generation change if the magnetic field is increased times?
To complete the task, use the formulas:
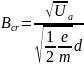
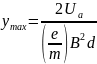
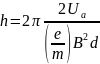
and the law of conservation of total energy.
Given:
d = 4,4 mm
= 5,7 kV
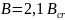
Solution:
Calculation of critical magnetic induction:
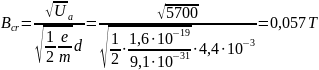
Calculation of the cyclotron frequency and the height of the cathode electron layer:
Calculation of magnetic field induction:
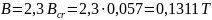
Calculation of cyclotron frequency:
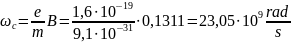
Calculation of the height of the cathode electrode layer:
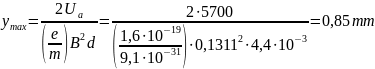
Calculation of the electronic trajectory step:
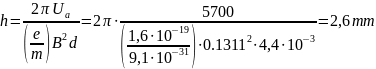
Potential at point ymax:
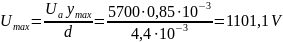
From the law of conservation:
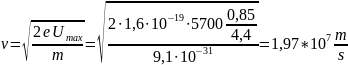
The frequency of magnetron generation when the magnetic field is increased by 1 time:
According
to the facts to change
the magnetic field is to change the magnetic induction (B). According
to the formula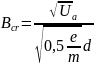 ,
we can notice, that magnetic induction depends on anode voltage (Ua).
These two quantities provide the necessary electron motion for
interaction with the resonator field. So, if we change magnetic
induction, we will violate
synchronism of the phase velocity of the wave and the average speed
of the electronic «spokes». As a result, the magnetron will no
longer generate a frequency.
,
we can notice, that magnetic induction depends on anode voltage (Ua).
These two quantities provide the necessary electron motion for
interaction with the resonator field. So, if we change magnetic
induction, we will violate
synchronism of the phase velocity of the wave and the average speed
of the electronic «spokes». As a result, the magnetron will no
longer generate a frequency.
Answer:
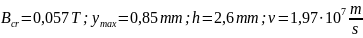
Sources: Lecture 8 materials; lecture 11 materials
Task 6.
Devices with dynamic control. Gyrosonance devices. Gyrotron.
Explain why gyrotrons are used mainly in the mm wavelength range. How the operation of the device is ensured at higher resonator modes. Describe how it is possible to get more output power.
Comment on the principle of operation of the gyrotron using the formula .
Calculate the parameters of the spiral trajectory of the electron beam of the gyrotron. Initial values for calculation (set, selectable):
• Accelerating beam voltage
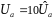 ,
where
,
where
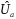 is the value of the
accelerating voltage from Problem No. 4
is the value of the
accelerating voltage from Problem No. 4
• The value of the frequency
of the microwave field f
from the condition
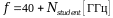
• The ratio of the
transverse and longitudinal velocity of the electron
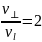
Defined values:
• The value of magnetic field induction B. Is it difficult to get such a field in practice?
Calculated from the cyclotron resonance condition
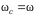 , where
, where
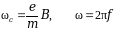 .
.
• Values of the total electron velocity and its longitudinal and transverse components
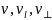 .
.
• The radius of the spiral
trajectory of the electron
 .
What should be the radius of the resonator?
.
What should be the radius of the resonator?
It is calculated from the condition of balance of centrifugal and magnetic forces.
• The time of one electron
revolution is the cyclotron period
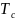
• The step of the spiral
trajectory is the cyclotron wavelength
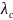
Answers:
1) Why gyrotrons are used mainly in the mm wavelength range?
Gyrotrons operate in the mm-band and at a high power level, such work requires a developed interaction space, but at the same time there is a need for selective excitation of the working type of oscillations. With increasing frequency, the wavelength of the radiation decreases (f=1/λ), which makes it possible to focus the radiation into a spot of the order of millimeters in size and achieve high energy flux densities affecting the material.
2) How the operation of the device is ensured at higher resonator modes?
The main problems of the gyrotron when working at higher modes are associated with the density of the spectrum of modes, while there is competition from the low harmonics. That is, the excitation of high harmonics requires at least a high Q-factor of the resonator. It is also possible to reduce the density of the natural frequency spectrum by using an open resonator.
3) Describe how it is possible to get more output power.
The total efficiency of the
gyrotron is defined as the ratio of the RF field energy given by the
device to the output waveguide to the energy supplied to the device
from the anode voltage source (for the same time interval). As in
other types of electronic devices, the total efficiency can be
represented as the product of the electronic efficiency
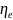 and the efficiency of the resonator
and the efficiency of the resonator
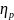
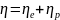
The efficiency of the
resonator can be expressed in terms of the loaded
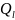 ,
external
,
external
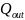 and own
and own
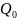 Q factor of the resonator:
Q factor of the resonator:
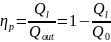
The value of loaded can, in turn, be expressed in terms of its own
and external of Q-factor:
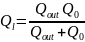
In relation to an open
waveguide type resonator, the intrinsic Q-factor is defined as the
ohmic Q-factor
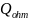 ,
which characterizes energy losses in the walls of the resonator, and
the external Q-factor is identified with the diffraction Q-factor of
the resonator
,
which characterizes energy losses in the walls of the resonator, and
the external Q-factor is identified with the diffraction Q-factor of
the resonator
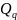 ,which
characterizes the loss of energy to radiation. Since the radiated in
this case, the energy is directed to the output waveguide and
represents the output energy of the device, then the diffraction
Q-factor plays the role of external Q-factor.
,which
characterizes the loss of energy to radiation. Since the radiated in
this case, the energy is directed to the output waveguide and
represents the output energy of the device, then the diffraction
Q-factor plays the role of external Q-factor.
Thus, for the loaded Q-factor and efficiency of the resonator, we obtain the following formulas:
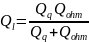
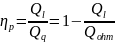
In the case of an open-type
resonator formed by a segment of a cylindrical waveguide with a
working wave type H01, the ohmic Q-factor is calculated by the
formula:
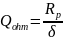 ,
where
,
where
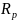 -resonator
radius;
-resonator
radius;
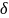 -
the thickness of the skin layer, determined by the formula:
-
the thickness of the skin layer, determined by the formula:
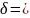 ,
where
,
where
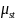 and
and
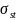 - specific electrical conductivity and magnetic permeability of the
resonator walls.
- specific electrical conductivity and magnetic permeability of the
resonator walls.
The diffraction Q - factor of oscillations of the form H011 is expressed by the formula:
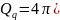 or
because
or
because
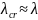 ,
we get:
,
we get:
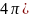
where
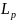 is the length of the working part of the resonator;
is the length of the working part of the resonator;
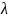 is the wavelength of the electromagnetic field,
is the wavelength of the electromagnetic field,
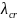 is the critical wavelength of type H01 in a cylindrical waveguide
forming the working part of the resonator;
is the critical wavelength of type H01 in a cylindrical waveguide
forming the working part of the resonator;
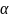 is a coefficient depending on the configuration of the resonator and
the geometry of the output window.
is a coefficient depending on the configuration of the resonator and
the geometry of the output window.
In cases where the significantly (several times) exceeds the diffraction Q factor , turns out to be close to unity. The output power is determined by the power of the electron beam and the value of the total efficiency of the device:
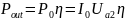
where
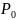 and
and
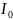 are the power and current of the electron beam;
are the power and current of the electron beam;
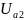 is the potential of the second anode.
is the potential of the second anode.
The high output power is due to the high energies of the electron flux of the order of hundreds of thousands of electron volts, and already the transition to the region of relativistic energies.
