
9201_Рауан_ЛР3
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра фотоники
отчет
по лабораторной работе №3
по дисциплине «Физика твердого тела»
Тема: Исследование температурной зависимости электропроводности полупроводников
Вариант №12
Студент гр. 9201 |
|
Рауан М. |
Преподаватель |
|
Васильева А.В. |
Санкт-Петербург
2021
Цель работы: изучить механизмы рассеяния носителей заряда в полупроводниках, определяющие температурную зависимость подвижности электронов. Рассчитать зависимость электропроводности полупроводников от температуры.
Основные теоретические сведения
Зависимость проводимости от температуры определяется температурными зависимостями концентрации и подвижности. Для невырожденных и собственных полупроводников концентрация носителей зависит от температуры и других внешних воздействий. Если температура постоянна и никакие поля на полупроводник не воздействуют, то такое состояние называется термодинамически равновесным. Такие носители заряда получили название равновесных.
Температурная зависимость концентрации носителей заряда для нескольких образцов с разной концентрацией донорной примеси имеет вид:
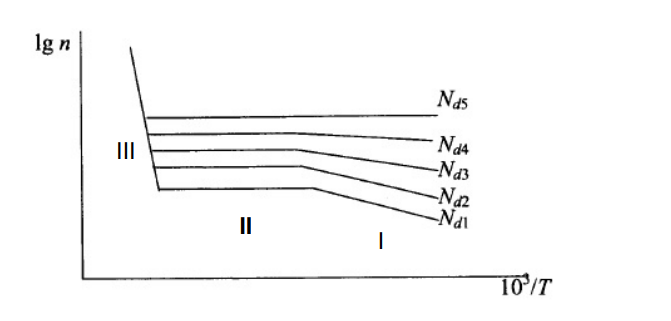
Рисунок 1 – Температурная зависимость концентрации носителей заряда в легированном полупроводнике
Зависимость в общем виде имеет 3 участка:
Область I – примесной проводимости (ионизации примеси);
Область II – истощения примеси;
Область III – собственной проводимости.
Тангенс
угла наклона прямой пропорционален
ширине запрещенной зоны полупроводника
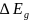 .
Температурная зависимость концентрации
свободных носителей заряда, построенная
в координатах Аррениуса, наглядно
показывает характер физических процессов,
происходящих при изменении температуры.
Это позволяет рассчитать параметры
полупроводникового материала: энергию
ионизации донорной примеси
.
Температурная зависимость концентрации
свободных носителей заряда, построенная
в координатах Аррениуса, наглядно
показывает характер физических процессов,
происходящих при изменении температуры.
Это позволяет рассчитать параметры
полупроводникового материала: энергию
ионизации донорной примеси
 и ширину запрещенной зоны.
и ширину запрещенной зоны.
Экспоненциальный закон изменения концентрации свободных носителей заряда при изменении температуры обусловливает принципиальное различие между температурной зависимостью проводимости полупроводников и металлов. У последних концентрация свободных носителей от температуры практически не зависит.
Температурная зависимость подвижности определяется, очевидно, температурной зависимостью времени релаксации, которая, в свою очередь, зависит от конкретного механизма рассеяния носителей заряда. Наиболее часто реализуются два вида рассеяния: на тепловых колебаниях в узлах кристаллической решетки (для атомных полупроводников – на акустических) и на ионизованной примеси.

Рисунок 2 – Температурная зависимость подвижности
Подводя итог, температурная зависимость электропроводности имеет вид:
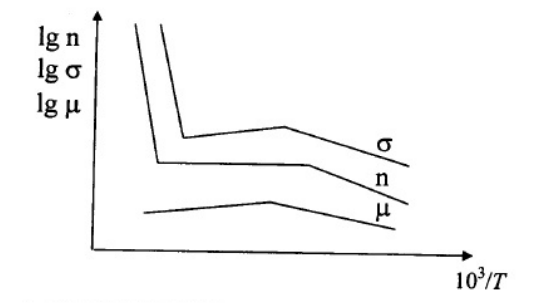
Рисунок 3 – температурная зависимость электропроводности
Экспоненциальная
зависимость
 позволяет
определить
в области низких температур и
в области собственной проводимости
аналогично тому, как эти величины
определяются из температурной зависимости
концентрации. Отметим, что ввиду малых
значений
при определении этой величины желательно
учитывать температурные зависимости
подвижности и предэкспоненциального
множителя в выражении для концентрации.
позволяет
определить
в области низких температур и
в области собственной проводимости
аналогично тому, как эти величины
определяются из температурной зависимости
концентрации. Отметим, что ввиду малых
значений
при определении этой величины желательно
учитывать температурные зависимости
подвижности и предэкспоненциального
множителя в выражении для концентрации.
Обработка результатов эксперимента
Для Ge с примесью Al (акцепторная примесь) расчет температурной зависимости химического потенциала при различных концентрациях и построение графика:
Воспользуемся численным решением уравнения электронейтральности:

Численное
решение относительно химического
потенциала
 позволяет построить его зависимость
от температуры при различных концентрациях:
позволяет построить его зависимость
от температуры при различных концентрациях:
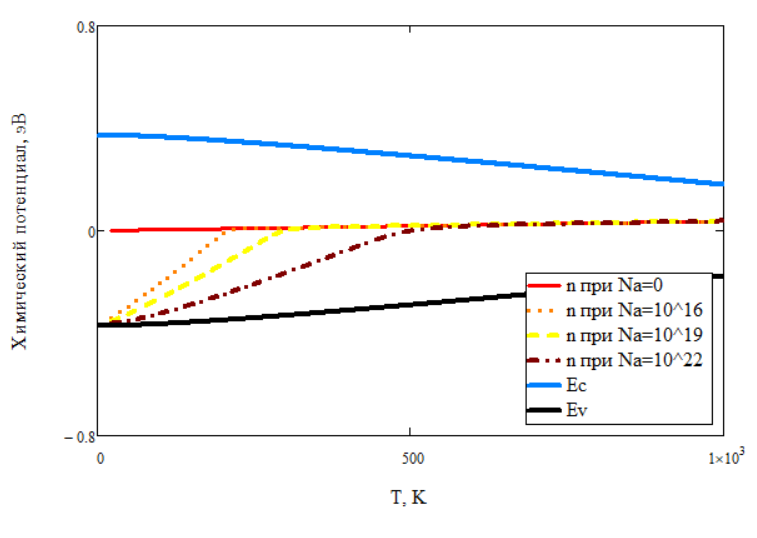
Рисунок 4 – Зависимость химического потенциала от температуры при различных значениях концентрации
При T = 510 K рассчитаем значения химического потенциала и получим:


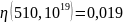

Расчет температурных зависимостей концентраций электронов, дырок, ионизированных и нейтральных примесей, построение графика данной зависимости при различных концентрациях примеси:
В невырожденном полупроводнике концентрации электронов и дырок определяются по формулам:


для
расчетов необходимы значения:
 .
.
Концентрация ионизированных акцепторов:

Построим соответствующие зависимости:

Рисунок 5 – Температурные зависимости концентраций электронов, дырок, общего количества примесей, ионизированных и нейтральных примесей, построенные для уровня легирования 0 1/м3

Рисунок 6 – Температурные зависимости концентраций электронов, дырок, общего количества примесей, ионизированных и нейтральных примесей, построенные для уровня легирования 1016 1/м3

Рисунок 7 – Температурные зависимости концентраций электронов, дырок, общего количества примесей, ионизированных и нейтральных примесей, построенные для уровня легирования 1019 1/м3
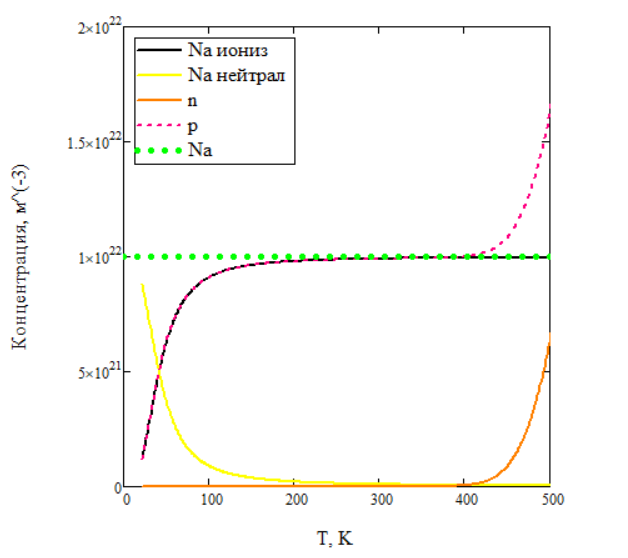
Рисунок 8 – Температурные зависимости концентраций электронов, дырок, общего количества примесей, ионизированных и нейтральных примесей, построенные для уровня легирования 1022 1/м3
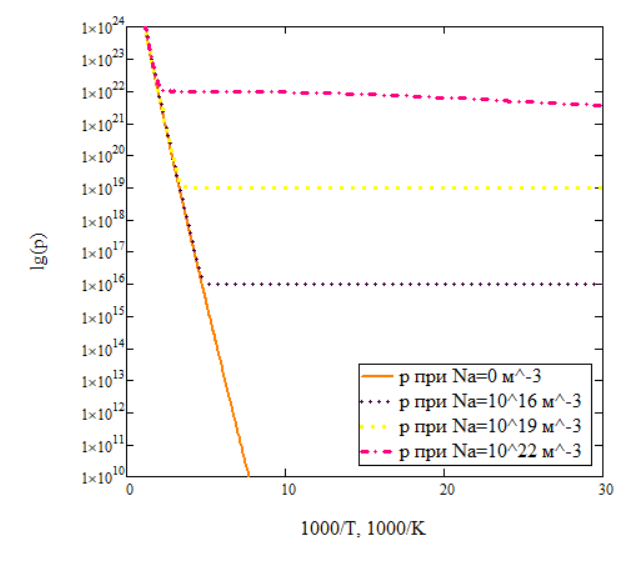
Рисунок 9 – температурные зависимости концентрации дырок
Построение графиков температурной зависимости подвижности электронов и дырок, отвечающих различным механизмам рассеяния. Расчет результирующей температурной зависимости подвижности.
Рассеяние носителей заряда на колебаниях кристаллической решетки:
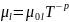
Для
Ge: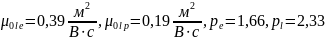
Рассеяние на ионах примеси:

Рассеяние на нейтральных примесях:

Результирующая подвижность с учетом различных механизмов рассеяния:


Рисунок 10 – Температурные зависимости подвижностей электронов, отвечающих различным механизмам рассеяния, и температурная зависимость результирующей подвижности при концентрации примеси 1022 1/м3
Полученные зависимости для дырок на одном графике:
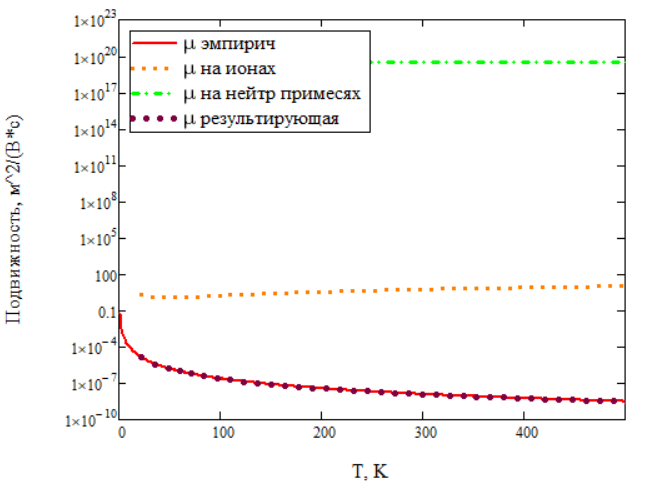
Рисунок 11 – Температурные зависимости подвижностей дырок, отвечающих различным механизмам рассеяния, и температурная зависимость результирующей подвижности при концентрации примеси1022 1/м3
Рассчитаем результирующую температурную зависимость подвижности электронов и дырок при различных концентрациях:
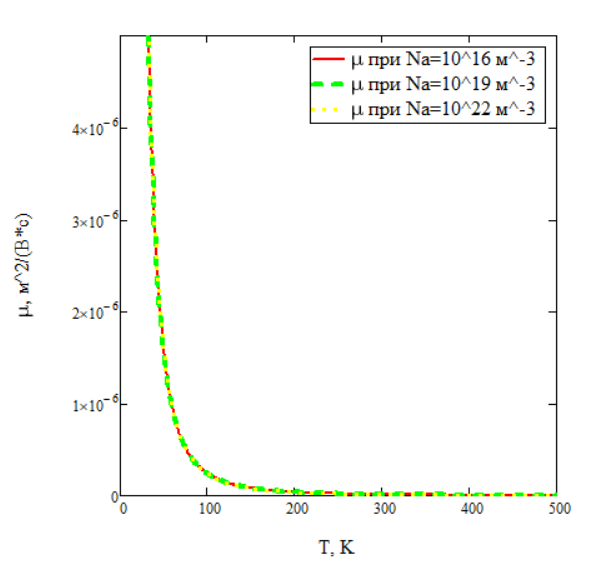
Рисунок 12 – Температурные зависимости результирующих подвижностей дырок при различных концентрациях примеси

Рисунок 13 – Температурные зависимости результирующих подвижностей электронов при различных концентрациях примеси
Расчет температурной зависимости проводимости Ge при нескольких концентрациях примеси:
Рассчитаем проводимость Ge по формуле:
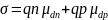
В качестве подвижностей электронов и дырок возьмем соответствующие результирующие подвижности:
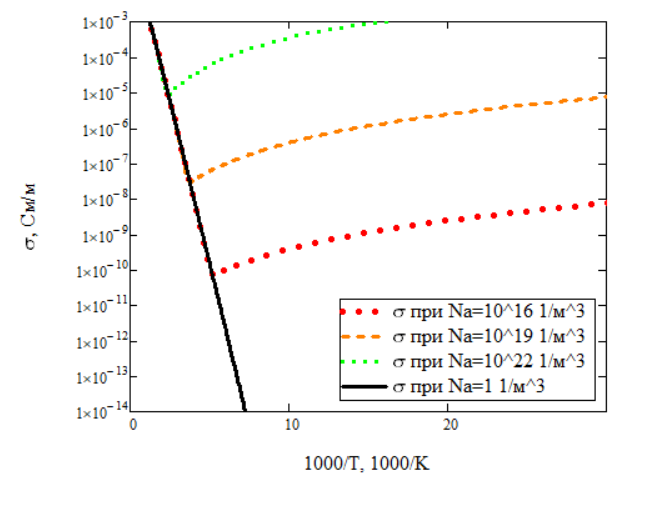
Рисунок 13 – Температурная зависимость проводимости Ge при различных значениях концентрации примеси, в координатах Аррениуса
Вывод: в данной лабораторной работе была изучена проводимость носителей заряда, подвижность, при различных механизмах рассеяния и сделаны следующие выводы:
Значение химического потенциала при увеличении температуры возрастает и стремится к середине запрещенной зоны полупроводника (рисунок 4).
По температурной зависимости подвижностей электронов и дырок (рисунок 10,11) можно сказать, что наибольший вклад в результирующую подвижность вносит рассеяние на узлах кристаллической решетки, поэтому подвижность не меняется при изменении концентрации примеси.
Объяснить температурную зависимость проводимости.
Температурная
зависимость подвижности определяется,
очевидно, температурной зависимостью
времени релаксации, которая, в свою
очередь, зависит от конкретного механизма
рассеяния носителей заряда. Наиболее
часто реализуются два вида рассеяния:
на тепловых колебаниях в узлах
кристаллической решетки (для атомных
полупроводников – на акустических) и
на ионизованной примеси. Теоретическое
рассмотрение дает зависимость
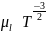 для
рассеяния на колебаниях решетки и
для
рассеяния на колебаниях решетки и
 для
рассеяния на ионизированной примеси.
Если в кристалле действуют оба механизма,
то
для
рассеяния на ионизированной примеси.
Если в кристалле действуют оба механизма,
то
 где
A и C – не зависящие от температуры
величины.
где
A и C – не зависящие от температуры
величины.

На рисунке приведена температурная зависимость подвижности, полученная при этих предположениях. При низких температурах доминирует примесное рассеяние, при высоких – тепловое.
