Книга об алгебре и алмукабале

Ал-Хорезми известен прежде всего своей « Книгой о восполнении и противопоставлении» («Ал-китаб ал мухтасар фи

хисаб ал-джабр ва-л-мукабала»), от названия которой произошло слово « алгебра».

В теоретической части своего трактата ал-Хорезми даёт классификацию уравнений 1-й и 2-й степени и выделяет шесть их видов:

•квадраты равны корням (пример 5x2 = 10x);

•квадраты равны числу (пример 5x2 = 80);

•корни равны числу (пример 4x = 20);

•квадраты и корни равны числу (пример x2 + 10x = 39);

•квадраты и числа равны корням (пример x2 + 21 = 10x);

•корни и числа равны квадрату (пример 3x + 4 = x2).

Такая классификация объясняется требованием, чтобы в обеих частях уравнения стояли положительные члены.

Охарактеризовав каждый вид уравнений и показав на примерах правила их решения, ал-Хорезми даёт геометрическое доказательство этих правил для трёх последних видов, когда решение не сводится к простому извлечению корня.

Другие работы

•Ал-Хорезми написал книгу «Об индийском счёте», способствовавшую популяризации десятичной позиционной системы записи чисел во всём Халифате, вплоть до Испании.

•Написанная ал-Хорезми «Книга картины Земли» — первое географическое сочинение на арабском языке — оказала сильное влияние на развитие этой науки.

•Главная заслуга ал-Хорезми в истории астрономии заключается в составлении тригонометрических и астрономических таблиц («Зидж ал-Хорезми»), которые послужили основой средневековых исследований в этой области как на Востоке, так и в Западной Европе.

•«Книга о построении астролябии» не сохранилась и известна только по упоминаниям в других источниках. Из астрономических сочинений ал-Хорезми известны также «Книга о солнечных часах» и «Книга о действии с помощью астролябии» (в неполном виде включённая в сочинение ал-Фаргани). В разделах 41-42 этой книги был описан специальный циркуль для определения времени намаза. Также Аль- Хорезми в 834 году отделил алгебру от геометрии

Абу Райхан Бируни

(перс. ینوریب دمحا نب دمحم ناحیروبا

4 сентября 973, город Кят, Хорезм, —

9 декабря 1048, Газни, совр. Афганистан ) — великий учёный из Хорезма, автор многочисленных капитальных трудов по истории, географии, филологии, астрономии, математике, геодезии, минералогии, фармакологии, геологии и др.

Главное сочинение Бируни по астрономии — «Канон Мас‘уда по астрономии и звёздам». План этого сочинения близок к стандартному плану арабских зиджей, но в отличие от них здесь приведены подробные экспериментальные и математические доказательства всех излагаемых положений

Большое внимание Бируни уделял математике, особенно тригонометрии: помимо значительной части «Канона Мас‘уда», он посвятил ей сочинения «Об определении хорд в круге при помощи вписанной в него ломаной линии» (здесь рассматривается ряд принадлежащих Архимеду теорем, не сохранившихся в греческих рукописях), «Об индийских рашиках» (в этой книге обсуждается так называемое тройное правило), «Сферика», «Книга жемчужин о плоскости сферы» и др. Вопросам прикладной математики посвящены трактат «Тени», несколько трактатов об астролябии и других астрономических инструментах, ряд сочинений погеодезии.

В 1038 году Бируни написал «Минералогию, или Книгу сводок для познания драгоценностей», в которой определён удельный вес многих минералов и даны подробные сведения о более чем пятидесяти минералах, рудах, металлах, сплавах и др. Им же составлена «Фармакогнозия» — книга о медицинских лекарствах.

Достижения аль-Бируни огромны,

отметим важнейшие:

•– изготовил один из первых научных глобусов, на котором были отмечены населенные пункты, так что можно было определять их координаты;

•– сконструировал несколько приборов для определения географической широты, которые описал в «Геодезии»: широта Бухары, по его данным, 39° 20', по современным – 39° 48'; широта Чарджоу соответственно 39° 12' и 39° 08';

•– тригонометрическим способом определил радиус Земли, получив примерно 6403 км (по современным данным – 6371 км);

•– определил угол наклона эклиптики к экватору, установив его вековые изменения. Расхождения между его данными (1020 г.) и современными составляют 45'';

•– оценил расстояние до Луны как 664 земных радиуса;

•– составил каталог 1029 звезд, положения которых вычислил заново из более ранних арабских зиджей;

•– считал Солнце и звезды огненными шарами, Луну и планеты – темными телами, отражающими свет; утверждал, что звезды в сотни раз больше Земли и подобны Солнцу;

•– заметил существование двойных звезд;

•– создал шаровую астролябию, что позволило следить за восходом и заходом звезд, за их движением на разных широтах и решать большое число задач.

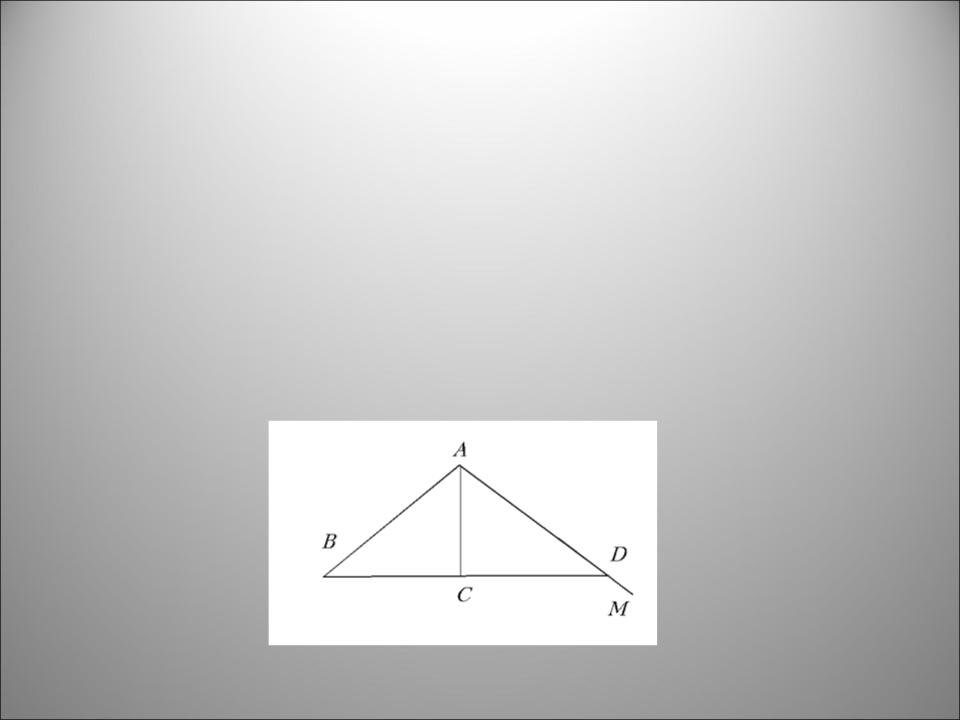
Чтобы определить ширину оврага ВС, аль-Бируни предлагает построить два прямоугольных треугольника АВС и ACD с общей стороной АС. Наблюдатель в точке А при помощи астролябии измеряет угол ВАС и строит такой же – САМ. Точку на отрезке АМ закрепляет вехой. После этого, продолжив направление прямой ВС в сторону вехи М, отыскивает точку D, которая лежит на пересечении ВС и АМ. Теперь измеряет DC, это расстояние равно искомому расстоянию ВС.

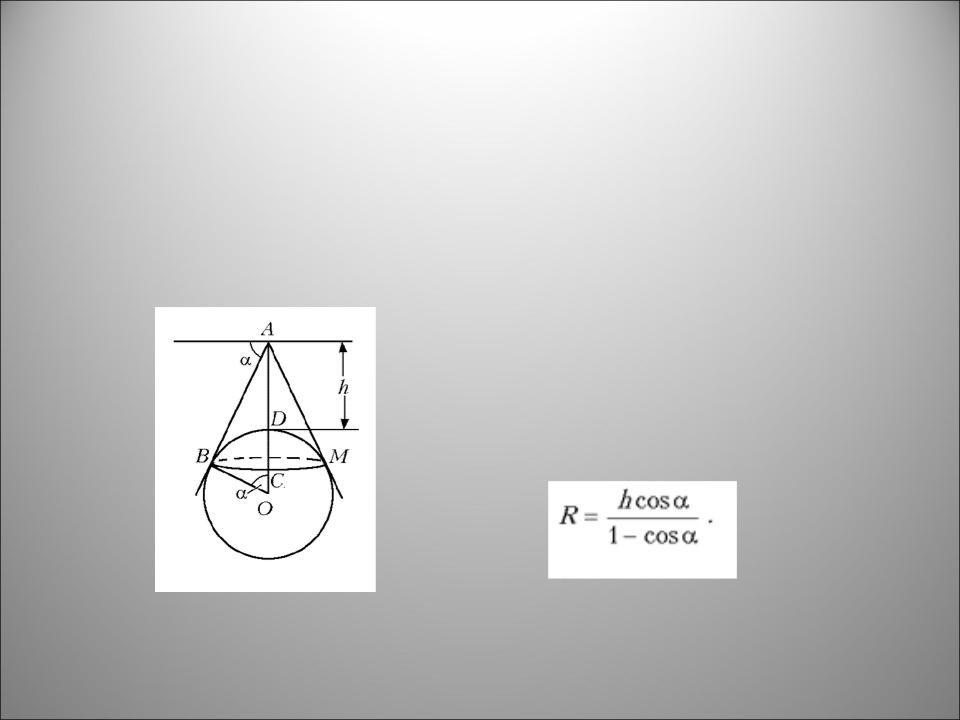
Измерить радиус Земли аль-Бируни удалось во время поездки в Индию. Угол «понижения горизонта» а он определил с помощью астролябии, а высоту горы, с которой производил измерения, – с помощью сконструированного им высотомера. Пусть h = AD – высота горы, AB и AM – касательные к поверхности Земли, OD – радиус Земли, CMB – видимый горизонт

Из рисунка видно, что R=(R+h)cosa,

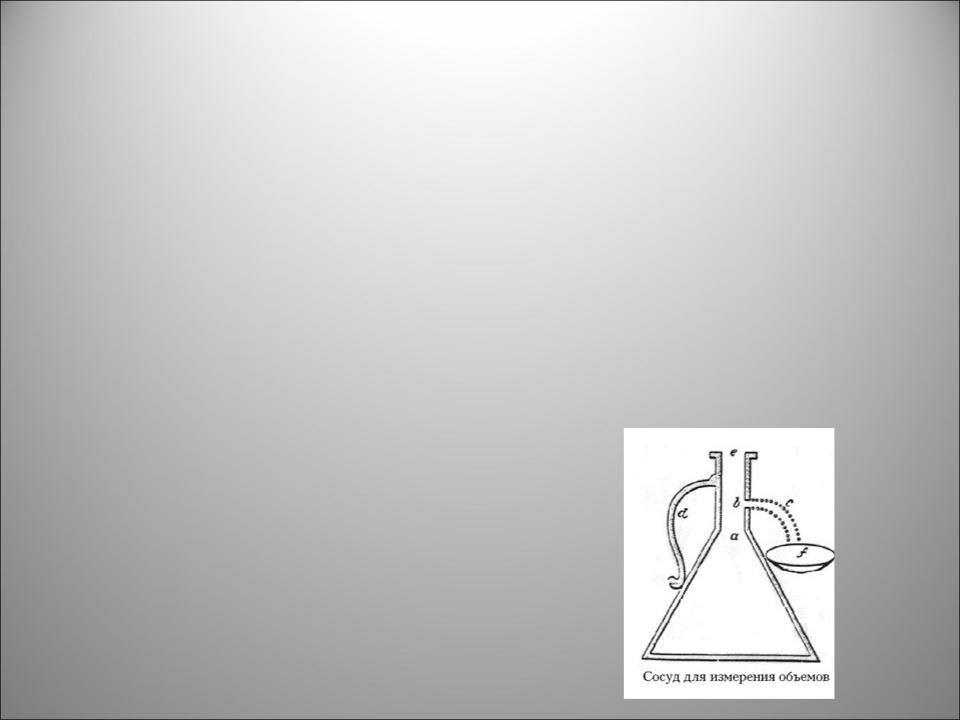
Заслугой аль-Бируни является определение удельных весов (плотностей) драгоценных камней и металлов. Для измерения объема им был сконструирован отливной сосуд. Измерения отличались высокой точностью (сравните данные аль-Бируни и современные в г/см3):

– золото: 19,05 и 19,32; – серебро: 10,43 и 10,50; – медь: 8,70 и 8,94; – железо: 7,87 и 7,85; – олово: 7,32 и 7,31.

Али ибн Иса ал-Аструлаби ал Харрани (IX в.)

— математик и астроном из Харрана, работал в Багдаде при халифе ал-Мамуне, участвовал в наблюдениях в Багдаде и Дамаске и в измерении длины 1° земного меридиана на равнине Синджар.

Написал «Трактат о действиях с астролябией», по которому получил своё прозвище. Составил также «Трактат о действиях с лунным тимпаном и диском затмений», «Книгу о тимпане горизонтов» и направленный против астрологии «Трактат об опровержении искусства приговоров звёзд».