1. Определение 7 логических функций

2. Правило поглощения, Блейка и де Моргана

3. Определение полного набора и базиса

4. Теорема поста на уровне таблицы поста

5. Сказать какие наборы называются сравнимыми

   1. . Определения монотонной, линейной и самодвойственной функции

6. Что такое сечение

7. Определение потока

8. Теорема Форда-Фалкерсона

9. Что такое насыщенное сечение

1. Определение 7 логических функций

Логической (булевой) функцией (или просто функцией) n переменных y = f(x1, x2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

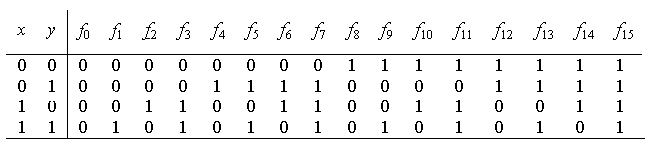
Перечислим 7 важнейших функций:

1) конъюнкция (функция И)

Заметим, что конъюнкция – это фактически обычное умножение (нулей и единиц). Иногда эту функцию обозначают x&y или xy;

2) дизъюнкция (функция или)

3) импликация (следование)

Иногда импликацию обозначают xy или x  y    (читается “из x следует y”).

Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если х = 0 (т. е. х “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если у = 1 (т. е. у “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию;

4) сложение по модулю 2 (здесь и далее, если не оговорено противное, знаком “+” мы будем обозначать такое сложение):

5) эквивалентность или подобие

Эта f₉ = 1 тогда и только тогда, когда х = у. Заметим, что будем применять оба обозначения: х^у (в основном при изучении функций) и х~ у (когда речь будет идти о логических операциях);

6) штрих Шеффера

Иногда эту функцию называют “не и” (так как она равна отрицанию конъюнкции);

7) стрелка Пирса (иногда эту функцию называют штрих Лукасевича)

Эта функция является отрицанием дизъюнкции и поэтому иногда ее называют “не или”.

2. Правило поглощения, Блейка, де Моргана.

1. Поглощение (“целое поглощает часть”):

х ху = х(1 у) = х.

2. Два распределительных закона:

х (y z) = x y  x z; х (y z) = (x y)(x z),

оба свойства могут быть доказаны простым рассуждением (например, если х = 0, тогда по свойству 1 справа выражение равно 0 и слева тоже 0, если х = 1, то справа стоит y z и слева будет то же самое).

3. Правила де Моргана:

оба эти правила обобщаются на любое число переменных:

4. Правило Блейка:

Пусть К₁ и К₂ – какие-то логические функции, тогда

что легко доказывается справа налево:

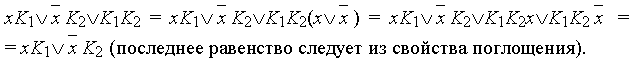
Следствием правила Блейка являются два правила обобщенного поглощения:

Заметим, что правила Блейка и следствия из него часто используются для упрощения дизъюнкции (см. разд. 5)

Замечание. Конъюнкция, дизъюнкция, отрицание были определены для объектов, принимающих лишь два значения 0 и 1. Однако бывают случаи, когда можно ввести такие операции для некоторых других объектов (эти операции также называют иногда конъюнкцией, дизъюнкцией и отрицанием), для которых также выполнены свойства 1–6. В этом случае говорят, что на этих объектах введена булева алгебра.

Например, пусть – некоторое множество точек (или элементарных событий в теории вероятности),  – множество подмножеств из  . Если A, B принадлежат  , то можно ввести сумму множеств (дизъюнкцию) A+B = AB (равную объединению точек из А и В), произведение множеств (конъюнкцию) АВ = А В (равное набору точек, входящих и в А, и в B одновременно) и дополнение (отрицание А), т. е. – множество точек из  , не входящих в А. Тогда для этих операций (и это легко проверить) будут выполнены свойства 1–6. Таким образом, множество всех подмножеств из  является булевой алгеброй