Пример 2.1. Найти объем пирамиды, ограниченной плоскостями

Найти объем пирамиды (см. рис. 6), ограниченной плоскостями: .

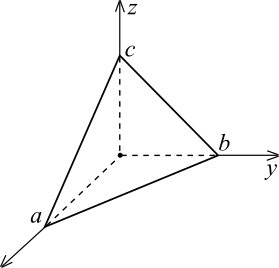
Рис. 6.

Решение. Область в двойном интеграле (2.3) для нашей пирамиды – треугольник с границами: , функция: . Тогда формула (2.7) принимает вид:

. ◄

2.4. Кроме вычисления объема (2.4) и площади (2.3) двойной интеграл можно применять для вычисления площади поверхности.

Пусть поверхность является графиком однозначной функции , определенной в области , причем частные производные

,

– непрерывные функции в этой области. В этом случае поверхность является гладкой, и ее площадь вычисляется с помощью интеграла вида (2.5), где роль подынтегральной функции играет . То есть площадь такой поверхности

. (2.10)