
- •2022 Г. СПбГут им. Проф. М. А. Бонч-Бруевича Санкт-Петербург, пр. Большевиков, д. 22
- •9. Несобственные интегралы.
- •9.1. Несобственный интеграл 1-го рода.
- •Пример 1. Интеграл сходится при и расходится при .
- •Пример 2. Интеграл .
- •Пример 3. Интеграл
- •Теорема 1.
- •Теорема 2.
- •Теорема 3.
- •Теорема 4.
- •Пример 4. Выяснить сходится или расходится интеграл
- •Теорема 5.
- •Пример 5. Исследовать на сходимость интеграл .
- •9.2. Несобственный интеграл 2-го рода.
- •Пример 1. Интеграл сходится при и расходится при .
- •Пример 2. Исследовать на сходимость интеграл .
- •Теорема 1.
- •Пример 3. При исследовать на сходимость интеграл (гамма-функцию)
- •Пример 4. Исследовать на сходимость и вычислить интеграл .
- •Литература
- •1. Функции нескольких вещественных переменных. Основные понятия
- •Пример 1.1. Найти частные производные функции
- •Пример 1.2. Найти частные производные второго порядка функции
- •Пример 1.3. В точке найти градиент функции
- •Пример 1.4. В точке найти производную по направлению градиента функции
- •Пример 1.5. Исследовать на экстремум функцию
- •Пример 1.6. В кольце найти наибольшее и наименьшее значения функции
- •2. Двойной интеграл
- •Пример 2.1. Найти объем пирамиды, ограниченной плоскостями
Теорема 1.
Если функция
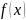 непрерывна на интервале
непрерывна на интервале
 ,
то интегралы
и
,
то интегралы
и
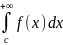 сходятся или расходятся одновременно
для любого
сходятся или расходятся одновременно
для любого
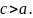
Доказательство
очевидно в
силу непрерывности функции
на интервале
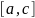 и равенства
и равенства
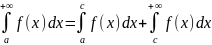 ■
■
Теорема 2.
Если функция
непрерывна на интервале
,
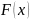 – ее первообразная, причем существует
конечный предел
– ее первообразная, причем существует
конечный предел
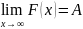 ,
то интеграл (9.1) сходится и равен
,
то интеграл (9.1) сходится и равен
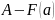 .
.
Доказательство следует из формулы Ньютона-Лейбница.■
Рассмотрим
несобственный интеграл с положительной
подынтегральной функцией. В этом
случае (см.п.8.2) интеграл с переменным
верхним пределом
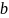 является возрастающей функцией аргумента
.
Тогда из теоремы о пределе монотонной
функции (п.2.3) следует
является возрастающей функцией аргумента
.
Тогда из теоремы о пределе монотонной
функции (п.2.3) следует
Лемма.
Если существует
постоянная
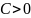 такая, что для любого значения
такая, что для любого значения
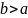 выполнено неравенство
выполнено неравенство
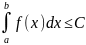 ,
,
то интеграл сходится, причем
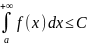 .
.
В противном случае интеграл расходится.■
На эту лемму опирается доказательство теорем, которые называются признаками сходимости.
Теорема 3.
Пусть функции
и
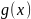 непрерывны на интервале [
непрерывны на интервале [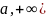 .
Пусть существует интервал [
.
Пусть существует интервал [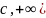 ,
,
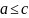 ,
на котором выполнено неравенство
,
на котором выполнено неравенство
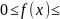 .
Тогда:
.
Тогда:
1) если расходится
интеграл
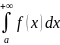 ,
то расходится и интеграл
,
то расходится и интеграл
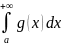 ;
;
2) если сходится интеграл , то сходится и интеграл .
Доказательство. Докажем второе утверждение, доказательство первого из него следует методом «от противного».
Пусть
сходится интеграл
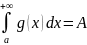 .
Тогда из теоремы 1 следует, что сходится
интеграл
.
Тогда из теоремы 1 следует, что сходится
интеграл
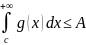 ,
и для любого
,
и для любого
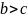 интеграл
интеграл
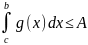 .
Из условия
и (8.10) следует, что
.
Из условия
и (8.10) следует, что
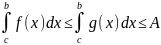 .
.
Остается сослаться на лемму и теорему 1. ■
Теорема 4.
Пусть функции
и
непрерывны на интервале [
,
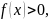
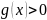 и
и
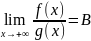 ,
,
где
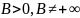 .
Тогда интегралы
и
сходятся
или расходятся одновременно.
.
Тогда интегралы
и
сходятся
или расходятся одновременно.
Доказательство.
Зададим число
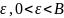 .
Для этого числа
.
Для этого числа
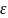 существует число
существует число
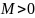 такое, что из неравенства
такое, что из неравенства
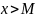 следует неравенство
следует неравенство
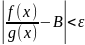 .
Последнее неравенство равносильно
системе неравенств:
.
Последнее неравенство равносильно
системе неравенств:
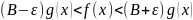 .
.
Остается сослаться на теоремы 1 и 3. ■
На практике в качестве функции сравнения удобно использовать степенную функцию. Это следует из примера 1.
Пример 4. Выяснить сходится или расходится интеграл
Решение. Для
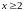 очевидна оценка подынтегральной функции:
очевидна оценка подынтегральной функции:
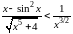 .
.
Так как
 сходится,
то сходится и заданный интеграл.◄
сходится,
то сходится и заданный интеграл.◄
Для произвольной
(знакопеременной) непрерывной функции
доказано (см. [2]) утверждение: если
сходится интеграл
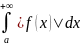 ,
то сходится и интеграл
.
■
,
то сходится и интеграл
.
■
Это утверждение позволяет ввести два новых понятия для интегралов от функций, которые принимают значения любого знака.
Несобственный интеграл называется абсолютно сходящимся, если сходится интеграл .
Несобственный интеграл называется неабсолютно или условно сходящимся, если он сходится, а интеграл расходится.
Для абсолютно сходящихся интегралов верна теорема, которая является следствием теоремы 3.
Теорема 5.
Пусть функции
и
(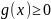 )
непрерывны на интервале [
.
Пусть
)
непрерывны на интервале [
.
Пусть
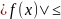 .
Тогда, если сходится интеграл
,
то абсолютно сходится интеграл
,
причем
.
Тогда, если сходится интеграл
,
то абсолютно сходится интеграл
,
причем
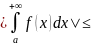 .
■
.
■
Пример 5. Исследовать на сходимость интеграл .
Решение.
Очевидна оценка подынтегральной функции:
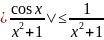 .
Интеграл
.
Интеграл
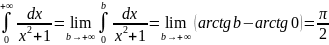 .
.
Следовательно, интеграл сходится абсолютно, причем
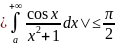 .
◄
.
◄
