Добавил:

DANiilPESHov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Высшая математика

Файл:

8. Определённый интеграл

.pdf

Скачиваний:

Добавлен:

07.03.2023

Размер:

410.99 Кб

Скачать

☆

8. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

8.1. Определение и свойства

Пусть функция ( ) принимает конечные значения в любой точке

замкнутого интервала [ ; ], < . Разобьём промежуток [ ; ] точками

0 =

, , , , … ,

на

интервалы

[ ; ], [ ; ],

−1

0 1

[ ;

], … , [

;

Обозначим через ∆ длину -того интервала:

∆

−1

−

, = 1, 2, … , . В каждом -том интервале выберем произвольную

−1

точку . Составим сумму

= ∑

(

) ∆ .

(8.1)

Сумма (8.1) называется и н т е г р а л ь н о й суммой для заданной функции

( ) и интервала [ ; ]. Введем ранг разбиения:

λ = max ∆ , = 1, … , ,

(8.2)

и устремим λ к нулю. Если при λ → 0 существует конечный предел у интегральной суммы (8.1), не зависящий ни от способа разбиения, ни от

выбора точек		, то он называется о п р е д е л е н н ы м и н т е г р а л о м		о т

ф у н к ц и и ( )		п о п р о м е ж у т к у [ ; ] и обозначается
		∫	( ) .

Функция	( ) называется в		этом случае и н т е г р и р у е м о й	н а
и н т е р в а л е [ ; ].
В качестве определения удобно взять следующую формулу:
		∫ ( ) = − ∫ ( ) #8.3		(8.3)

А также		∫ ( ) = 0.
		∫ ( ) = 0.		(8.4)

К понятию определённого интеграла приводят многие физические и геометрические задачи, в частности, задача о вычислении площади криволинейной трапеции.

Рассмотрим фигуру (она называется криволинейной трапецией), ограниченную вертикалями = , = , осью и графиком функции =( ), принимающей положительные значения и непрерывной на интервале [ ; ]. В этом случае интегральная сумма (8.1) равна площади ступенчатой (заштрихованной) фигуры, близкой к криволинейной трапеции (рис. 20).

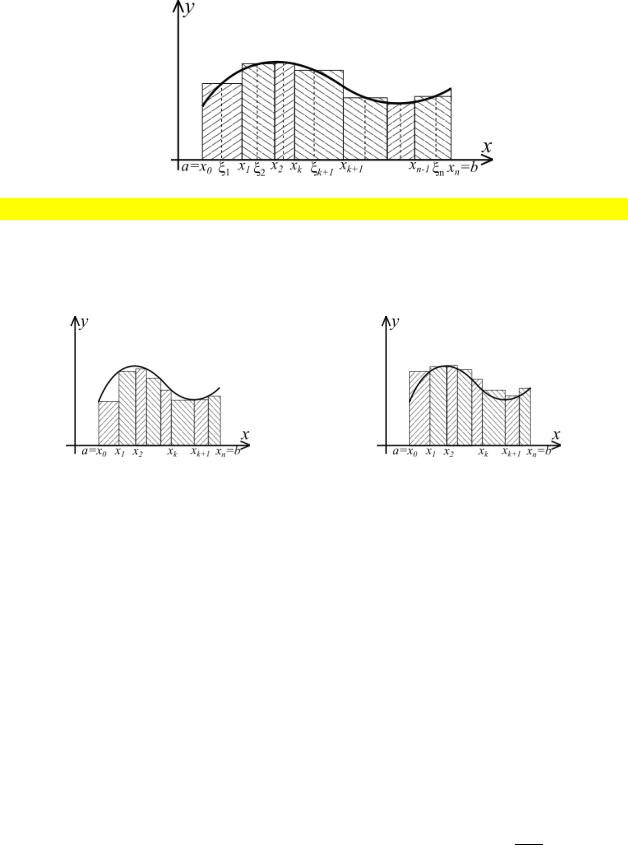
Рис. 20

Построим для данного разбиения еще две суммы: (1)

= ∑

∆

(2)

= ∑

∆

, где

– наименьшее значение функции ( ),

наибольшее значение на интервале [

; ].

−1

–

		Рис. 21.
Очевидно (см. рис. 21) выполнение двух неравенств:
(1)	≤	≤ (2), (1)		≤ ≤ (2),	(8.5)

где - площадь криволинейной трапеции.				Легко видеть, что при λ → 0
(дроблении на все меньшие интервалы)			сумма (1) возрастает,		оставаясь

ограниченной сверху в силу второго из неравенств (8.5), а сумма (2) убывает,

оставаясь ограниченной снизу. Тогда из теоремы о пределе монотонной

функции п.2.3 следует, что существуют пределы (1) =					lim (1)	и (2) =
					λ→0
lim (2), причем (1)					λ→0
lim (2), причем (1)		≤ ≤ (2).
λ→0
λ→0	Рассмотрим разность (2)		− (1)
	Рассмотрим разность (2)		− (1)	и докажем что она стремится к нулю при

λ → 0. Тогда из теоремы о пределе суммы следует равенство пределов (1) == (2).

Действительно, зададим число > 0, построим 1 = − . В силу непрерывности функции ( ) существует число > 0 такое, что при λ < δ

разность −			<	для любого интервала разбиения. Тогда
			1
(2)	− (1)	= ∑		(	− )∆	<	∑	∆	= ( − ) = .
			=1			1	=1		1

Следовательно, в силу первого из неравенств (8.5), по теореме о «сжатой переменной» п.2.2 существует предел интегральной суммы и, тем самым, определенный интеграл, и его значение совпадает с площадью криволинейной трапеции . То есть

= ∫	( ) .	(8.6) ■

Мы получили также, что положительная непрерывная функция является интегрируемой. Можно доказать (см. [2]), что интегрируемыми являются и непрерывные, и кусочно-непрерывные функции (т.е. функции, имеющие только конечное число разрывов 1-го рода), принимающие значения любого знака.

Приведем основные свойства определенного интеграла.

1) Так как определенный интеграл представляет собой число, зависящее только от подынтегральной функции и интервала, на котором она задана, то верно равенство

∫ ( ) = ∫ ( ) .

То есть определенный интеграл не зависит от обозначения переменной интегрирования. ■

2) Свойство линейности. Пусть функции 1( ) и 2( ) – интегрируемы на [ ; ], , - числа. Тогда

∫ (1( ) + 2( )) = ∫	1( ) + ∫ 2( ) .	(8.7)
Доказательство этого утверждения следует из определения
определенного интеграла и теоремы о пределе суммы. ■
3) Пусть подынтегральная функция ( ) = = , тогда
∫ = ( − ).		(8.8)

Доказательство формулы (8.8) следует из того, что в данном случае интегральная сумма (8.1) равна ( − ) и не зависит ни от способа разбиения, ни от выбора точек . ■

Следствие. В частности, если = 1, то ∫ = − , если = 0, то

∫ 0 = 0.

4) С в о й с т в о а д д и т и в н о с т и .		Пусть < < , функция ( ) –
интегрируема на всех трех интервалах [ ; ], [ ; ] и [ ; ]. Тогда
∫	( ) = ∫	( ) + ∫ ( ) .	(8.9)

Доказательство этого утверждения также следует из определения определенного интеграла и теоремы о пределе суммы, причем в качестве одной из точек разбиения следует взять точку . ■

Следствие. Используя формулы (8.3) и (8.4) можно доказать, что формула (8.9) будет верна при любом расположении чисел , и .

8.2. ИНТЕГРИРОВАНИЕ НЕРАВЕНСТВ.

Теорема 1. Пусть функции 1( ) и 2( ) – интегрируемы на [ ; ], < ,

причем 1( ) ≤ 2( ) при [ ; ]. Тогда
∫	( ) ≤ ∫		( ) .	(8.10)
	1		2
Доказательство следует из определения определенного интеграла и
теоремы о предельном переходе в неравенстве. ■
Следствие. Пусть функция ( )		– интегрируема на [ ; ], < ,		( ) ≥
0 при [ ; ]. Тогда
∫ ( ) ≥ 0.				(8.11)

Замечание. Если интегрируемая функция ( ) удовлетворяет строгому неравенству ( ) > 0 при [ ; ], нельзя утверждать, что вместо (8.11) будет выполняться строгое неравенство для интеграла. Но для непрерывных функций такое утверждение верно.

Теорема 2. Пусть функция ( ) – непрерывна на [ ; ], < , ( ) > 0 при [ ; ]. Тогда

∫	( ) > 0.	(8.12)

Доказательство. По теореме Вейерштрасса существуют наименьшее ( ) и наибольшее ( ) значения функции ( ), которые достигаются на [ ; ], причем в силу условия теоремы > 0, > 0. Тогда из теоремы 1 и (8.8) получается, что

	( − ) ≤ ∫ ( ) ≤ ( − ),				(8.13)

откуда и следует утверждение теоремы. ■
Следствие. Пусть функции 1( ) и			2( ) – непрерывны на [ ; ], < ,
причем 1( )	< 2( ) при [ ; ]. Тогда
	∫	( ) < ∫		( ) .	(8.14)
		1		2

Замечание. Неравенство (8.13) верно для любой (принимающей значения любого знака) непрерывной функции.

Теорема 3. Пусть функция ( ) – интегрируема на промежутке [ ; ], <. Тогда

\|∫	( ) \| ≤ ∫ \| ( )\| .	(8.15)

Доказательство следует из определения определенного интеграла, неравенства для модулей, называемого неравенством треугольника и теоремы

определьном переходе в неравенстве. ■

8.3.ТЕОРЕМА О СРЕДНЕМ И ЕЕ ОБОБЩЕНИЕ

Теорема. Пусть функции ( ) и ( ) – непрерывны на [ ; ], < , причем функция ( ) сохраняет знак на [ ; ]. Тогда существует (хоть одно) число : < < , такое что

∫	( ) ( ) = ( ) ∫	( ) .	(8.16)

Доказательство. Пусть сначала ( ) > 0. Аналогично с (8.13) имеет место

неравенство
∫ ( ) ≤ ∫ ( ) ( ) ≤ ∫ ( ) .						(8.17)

Разделим неравенство (8.17) на интеграл ∫ ( ) , который в силу (8.12) является
положительным числом. Получим неравенство ≤ ≤ , где
			∫ ( )( )
	=				.
	=		∫ ( )		.
			∫ ( )

По теореме Больцано-Коши существует хотя бы одно число , < < , такое что
( ) = .
Если функция ( ) < 0, то введем функцию				̃
Если функция ( ) < 0, то введем функцию				( ) = − ( ) > 0, для которой, как
доказано, верно равенство (8.16). То есть
∫ ( )(− ( )) = ( ) ∫ (− ( )) .

Остается сократить на (-1). ■
Следствие (теорема о среднем). В частности, если ( ) = 1, а ( ) -
непрерывна на [ ; ], < , то существует число : < < такое, что
∫ ( ) = ( )( − )						(8.18)

или
1		∫ ( ) = ( ).				(8.19)
	−	∫ ( ) = ( ).				(8.19)
	−
(Выражение в левой части равенства				(8.19) называется с р е д н и м
з н а ч е н и е м функции ( ) по промежутку [ ; ]).
Геометрически равенство (8.18)			означает, что существует такое число
: < < , что площадь криволинейной трапеции (8.5) равна						площади

прямоугольника с основанием [ ; ] и высотой, равной ( ) (см. рис.22).

Рис. 22. Геометрическая интерпретация теоремы о среднем

8.4. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА

Теорема Барроу. Пусть функция ( ) непрерывна на интервале [ , ]. Введем функцию

(	)		( ) ,	[	, .	(8.20)
		= ∫
					]

Тогда

′( ) = ( ).

То есть интеграл с переменным верхним пределом (8.20) от непрерывной функции является первообразной подынтегральной функции.

Доказательство. Пусть x > 0 . Рассмотрим

( +∆ )− ( )		=	1	(∫+∆	( ) − ∫	( ) ) =
∆			∆

= ∆1 (∫ ( ) + ∫ +∆ ( ) − ∫ ( ) ) = ∆1 ∫ +∆ ( ) .

По теореме о среднем существует такая точка ̅ [ , + ∆ ], что

+∆

∫( ) = ( ̅)∆ .

Тогда

( +∆ )− ( ) = ( ̅).

∆

Из условия ̅ [ , + ∆ ] следует, что если ∆ → 0, то ̅→ . Поскольку функция( ) непрерывна, то из того, что ̅→ , следует, что ( ̅)→ ( ). Тем самым доказано существование предела справа. Аналогично доказывается, что предел слева существует и совпадает с пределом справа. Тогда

′( ) = lim	( + ∆ ) − ( )	=	lim ( ̅)= ( ).
′( ) = lim	∆	=	lim ( ̅)= ( ).
∆ →0	∆		∆ →0
Теорема доказана. ■
Из теоремы Барроу вытекает формула			Ньютона – Лейбница -

способ вычисления определённого интеграла ∫ ( ) в случае непрерывной

подынтегральной функции.

Теорема. Пусть функция ( ) непрерывна на интервале [ , ] и ( ) – ее первообразная ( ′( )= ( )). Тогда

∫

(

)

(

)

−

(

)

(8.21)

Доказательство. Для функции ( ), определенной формулой (8.20) верны свойства:

( ) = ∫ ( ) ,

( ) = ∫ ( ) = 0.

Следовательно,

∫ ( ) = ( ) − ( ).

(8.22)

Поскольку две первообразные функции ( ) отличаются на постоянную , и верно

очевидное равенство

( ) − ( ) = ( ( ) + ) − ( ( ) + ) = ( ) − ( ),

то в последнем равенстве (8.22) функцию

( ) можно заменить на

( ). Тогда, введя

обозначение (называемое подстановкой):

( ) − ( ) = ( )| ,

получим формулу (8.21). ■

Пример. Вычислить интеграл

x	3	dx

Решение. По формуле 1 таблицы 2 находим первообразную и подставляем пределы

4			4					5	4			5
4		3	4	3/2		2		5		2		5		62
	x	3	dx = x	3/2	dx =	2	x	2	=	2	4	2	−1 =	62
	x		dx = x		dx =		x		=		4		−1 =

1			1			5				5				5
1			1						1
									1

◄

8.5.ЗАМЕНА ПЕРЕМЕННОЙ И ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ

ВОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ

Теорема. (Замена переменной). Пусть две переменные , [ , ], и

, [ , ], связаны взаимно-однозначной зависимостью, т.е. известны две

взаимно-обратные функции: = ( ) и	= ( ),	причем = ( ), =
( ), = ( ), = ( ). Пусть функция ( ) и		её производная ′( )

непрерывны на интервале [ , ], функция ( ) непрерывна на интервале [ , ]. Тогда

(

)

(

( )

′

( ) =

(

)

− ( ) ,

(8.23)

∫

= ∫

)

где ( ) – первообразная функции

( ) = ( ( )) ′( ).

Доказательство следует из теоремы о замене в неопределенном

интеграле и формулы Ньютона-Лейбница. ■

Заметим, что

при

вычислении определённого

интеграла

можно

возвращаться к первоначальной переменной и пользоваться формулой (7.6). Но согласно приведенной теореме это не обязательно, достаточно пересчитать и подставить пределы интегрирования для переменной .

Пример 1. Вычислить интеграл

a	a
	a
	2

−

x	2	dx

																											0
Решение. Сделаем подстановку x = a sin t :
a											x = a sin t, dx = a cos tdt,																						/2					a	2 /2


			a2 − x2 dx = x = 0 t = 0,																												= a2 cos2 tdt =										(1+ cos 2t )dt =
			a2 − x2 dx = x = 0 t = 0,																												= a2 cos2 tdt =										(1+ cos 2t )dt =
0											x = a t =																					0			2						0
											x = a t =

																				2

	a2					1					2						2
=				t +			sin 2t							= a						.
=				t +			sin 2t							= a						.
		2				2						0							4
												0
Вычислим для сравнения этот интеграл с помощью первообразной,
найденной в примере 2 п. 7.4.
∫													2																							2								2
		√ 2			− 2				= (				2		arcsin						(			) +						√ 2		− 2)\| =				2	arcsin(1) =							2	. ◄
		√ 2			− 2				= (						arcsin						(			) +				2		√ 2		− 2)\| =			2		arcsin(1) =							4	. ◄
0													2															2				0			2									4
																																0
																											9				x
Пример 2. Вычислить интеграл																															x	dx .


																											4			x −1
																											4

Решение. Применив подстановку																									x = t , получаем
																		= t, x = t2 ,
					9											x																3 2t2			3
									x							x																										1
									x																																	1
											dx	=											x			4			9		=			dt = 2		t +1				+			dt =


							x −1							dx = 2tdt,																		t −1										t −1
							x −1							dx = 2tdt,																		t −1										t −1
					4																		t				2			3		2			2
																							t				2			3															◄
							t2															3
							t2															3
					= 2					+ t + ln (t −1)													= 7 + 2 ln 2.
					= 2			2		+ t + ln (t −1)													= 7 + 2 ln 2.
								2														2
																						2

Приведем два случая, в которых вычисление интеграла упрощается в силу симметрии подынтегральной функции.

Лемма 1. Пусть четная функция ( ) интегрируема на интервалах

[− , ], [− , 0] и [0, ]. Тогда

∫− ( ) = 2 ∫0 ( ) .

Лемма 2. Пусть нечетная функция ( ) интегрируема на интервалах

[− , ], [− , 0] и [0, ]. Тогда

∫− ( ) = 0.

Доказательство этих двух лемм проводится одинаково. Разбиваем промежуток [− , ] на две части [0, ] и [− , 0]. В интеграле ∫−0 ( )

делаем замену = − . Тогда для четной функции ( )

∫−0 ( ) = ∫0 ( ) ,

для нечетной –

∫−0 ( ) = − ∫0 ( ) ,

откуда и следуют утверждения лемм. ■

Теорема.	(Интегрирование по	частям).	Пусть	функции
( ), ( ), ′( ), ′( ) – непрерывны на [ ; ]. Тогда
∫	( ) ′( ) = ( ) ( )\|	− ∫ ( ) ′( ) .		(8.24)

Доказательство следует из теоремы об интегрировании по частям в
неопределенном интеграле и формулы Ньютона-Лейбница.			■

Пример. Вычислить интеграл

x cos

xdx

Решение. Применим формулу интегрирования по частям:


2	u = x,du = dx,			/2	2			/2
x cos xdx =	u = x,du = dx,	= x sin x		/2	− sin xdx =		+ cos x	/2
x cos xdx =	v = cos x, v = sin x	= x sin x	0		− sin xdx =	2	+ cos x	0
0	v = cos x, v = sin x				0	2
0					0

−1

.◄

Соседние файлы в папке 1сем

#
07.03.2023421.15 Кб704.1 Бесконечно малые и непрерывности2.pdf
#
07.03.2023445.37 Кб715. Производные.pdf
#
07.03.2023459.15 Кб696. Исследование функции.pdf
#
07.03.2023404.74 Кб697. Дифференциалы и интегралы функций.pdf
#
07.03.2023321.17 Кб687.6 - 7.8 Методы интегрирования.pdf
#
07.03.2023410.99 Кб698. Определённый интеграл.pdf
#
07.03.2023517.4 Кб688.6 Вычисление площади с помощью определённого интеграла.pdf