
ИСиТ / 09.03.02 Интеллектуальные информационные системы и технологии / 2 курс 2 семестр / Алексеев Александр Борисович / Высшая математика / Методички от Алексеева PDF (в порядке посылаемости) — копия / 1сем / 7. Дифференциалы и интегралы функций
.pdf
6.ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
6.1.ДИФФЕРЕНЦИАЛ ФУНКЦИИ 1-ГО ПОРЯДКА И ЕГО СВОЙСТВА
Пусть функция |
= ( ) дифференцируема |
в |
точке |
. |
|
Д и ф ф е р е н ц и а л о м |
1 - г о п о р я д к а |
ф у н к ц и и ( ) |
в |
этой |
точке |
называется |
|
|
|
|
|
|
= ′ или |
( ) = ′( ) , |
|
|
(6.1) |
где дифференциал независимой переменной равен ее приращению, то есть
= ∆.
Из формулы (6.1) следует, что производную ′( ) можно рассматривать как отношение дифференциалов .
Геометрический смысл дифференциала и его отличие от приращения функции видны на рисунке 19.
Рис. 19
Из (4.6) следует связь между приращением функции ∆ ( ) и ее
дифференциалом: |
|
∆ ( ) = ( ) + (∆ )∆, |
(6.2) |
где (∆ ) – бесконечно малая при ∆ → 0.
Следовательно, дифференциал отличается от приращения на бесконечно малую высшего порядка и используется поэтому в приближенных вычислениях вместо приращения функции.
Свойства 1-го дифференциала. 1. (( )) = ( ), = .

2.(( ) + ( )) = ( ) + ( ).
3.(( )( )) = ( )( ) + ( )( ).
4. (( )( )) = ( )( )− ( )( ).
5. Дифференциал 1-го порядка обладает свойством инвариантности, то есть выражение для дифференциала одинаково в случаях, когда х – независимая переменная или сама является функцией.
Доказательство. Пусть = ( ), = ( ).
Тогда по правилу дифференцирования сложной функции
= ( ( ( ))) = ′ ′ = ′ . ■
Доказательства остальных свойств дифференциала следуют из свойств производных (п. 4.2.2).
6.2. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ И ИХ СВОЙСТВА
Пусть функция = ( ) имеет производную –го порядка в точке .
Д и ф ф е р е н ц и а л о м - г о п о р я д к а ф у н к ц и и ( ) в этой точке называется дифференциал от дифференциала ( − 1)-го порядка, то есть
= (−1). |
(6.3) |
Так как приращение независимой переменной |
= ∆ играет роль |
постоянной, то |
|
= ( )( )( ) . |
(6.4) |
Из формулы (6.4) следует, что производную –го порядка ( )( ) также
можно рассматривать как отношение ( ).
Для дифференциалов высших порядков сохраняются свойства 1. и 2. Свойства 3. и 4. усложняются, так как усложняются формулы для производных высших порядков, в частности, свойство 3. записывается через биномиальные коэффициенты . Например,
2( ) = (′′ + 2′ ′ + ′′)( )2 = 2 + 2 + 2 . (6.5)
Свойство инвариантности 5. не сохраняется для дифференциалов высших порядков.

7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
7.1. ПЕРВООБРАЗНАЯ И ЕЕ СВОЙСТВА
Пусть функция ( ) определена на некотором конечном или бесконечном промежутке числовой оси. Функция ( ) называется первообразной функции ( ), если во всех внутренних точках промежутка функция ( ) имеет производную и
′( ) = ( ). |
(7.1) |
Легко проверить, что первообразная у функции не единственна.
Свойства первообразных одной функции сформулируем в виде двух теорем.
Теорема 1. Если функция ( ) – первообразная функции ( ), то и функция 1( ) = ( ) + , где - любая постоянная, также является первообразной той же функции ( ).
Доказательство. Условие (7.1) для функции 1( ) проверяется дифференцированием
1′( ) = ( ( ) + )′ = ′( ) + ′ = ( ) + 0 = ( ). ■
Верно и обратное утверждение.
Теорема 2. Пусть 1( ) и 2( ) – две первообразные одной функции ( ) на некотором промежутке. Тогда на этом промежутке
1( ) − 2( ) = ,
где – постоянная.
Доказательство. Введем функцию ( ) = 1( ) − 2( ). Очевидно, ее производная на нашем промежутке равна нулю:
′( ) = 1′( ) − 2′( ) = ( ) − ( ) = 0.
Остается сослаться на п. 5.2 (необходимое и достаточное условие постоянства функции). ■
7.2.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
Неопределенным интегралом от функции ( ) называется совокупность всех первообразных этой функции и обозначается
∫ ( ) . |
(7.2) |
Выражение ( ) в (7.2) называется подынтегральным выражением, а ( ) – подынтегральной функцией , процесс отыскания первообразных – интегрированием.
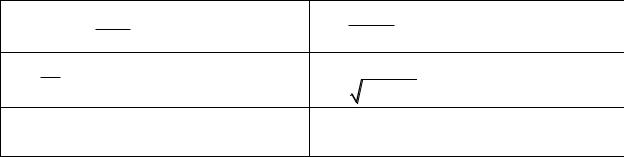
Из теорем 1 и 2 п. 7.1 следует, что неопределенный интеграл можно представить в виде
∫ ( ) = ( ) + , |
(7.3) |
где ( ) - какая-либо первообразная функции ( ), – произвольная постоянная. То есть, меняя в (7.3) постоянную , можно получить любую первообразную функции ( ).
В разделе «Определенный интеграл» будет доказано, что у
непрерывной функции ( ) существует первообразная. Не оговаривая особо,
в дальнейшем будем предполагать выполненным условие непрерывности подынтегральной функции.
Свойства неопределенного интеграла:
1.∫(( ) + ( )) = ∫ ( ) + ∫ ( ) , , −
,
2.(∫ ( ))′ = ( ),
3.(∫ ( )) = ( ) ,
4.∫ ′( ) = ( ) + ,
5.∫ ( ) = ( ) + .
Доказательство этих свойств проводится (согласно определению (7.3)) с помощью дифференцирования левой и правой частей равенства. ■
7.3. ТАБЛИЦА ИНТЕГРАЛОВ
Так как интегрирование есть действие, обратное дифференцированию, то таблица основных интегралов получается из таблицы производных 4.2.5.
1. |
|
x |
a |
dx |
|
||||
|
|
2.dxx =
3.exdx
|
x |
a+1 |
|
|
= |
|
, a −1 |
||
a |
+1 |
|||
|
|
ln  x
x + C, x 0
+ C, x 0
= ex + C
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
8. |
|
|
|
dx |
|
= −ctgx + C |
|
|
|
|
|||||||||
sin |
2 |
x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9. |
|
|
|
|
dx |
|
|
|
|
|
= arcsin |
x |
|
+ C, a 0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||
|
|
a |
2 |
− x |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
|
|
dx |
|
|
|
|
= |
1 |
arctg |
x |
+ C, a 0 , |
|||||||
x |
2 |
|
2 |
|
|
|
a |
||||||||||||
|
|
|
|
|
+ a |
|
|
|
|
|
a |
|
|
||||||

4. |
|
|
|
5. |
|
6. |
|
|
|
7. |
|
|
x |
|
|
a |
x |
|
|
a |
dx = |
|
+ C |
, a>0, a≠ 1 |
|||
|
|
||||||
|
ln a |
||||||
|
|
|
|
|
|
||
cos xdx = sin x + C |
|||||||
sin xdx = −cos x + C |
|||||||
|
dx |
= tgx + C |
|
||||
|
|
|
|||||
cos2 x |
|
||||||
11. |
|
chxdx = shx + C |
|||
|
|||||
12. |
|
shxdx = chx + C |
|||
|
|||||
13. |
|
1 |
|
dx = thx + C |
|
|
2 |
|
|||
|
|
|
|
||
|
|
ch |
|
x |
|
14. |
|
1 |
|
dx = −cthx + C |
|
2 |
|
||||
|
|
sh |
|
x |
|
Замечание. В силу тождеств: arcsin + arccos = /2 и arctg + arcctg = /2 неопределенные интегралы № 9 и № 10 могут быть записаны и через другие функции.
Пример 1. Пусть ( ) – первообразная функции ( ). Тогда для ≠ 0
∫ ( + ) = |
1 |
( + ) + , |
(7.4) |
|
Доказательство также проводится с помощью дифференцирования левой и правой частей равенства (7.4) и формулы (4.9). ◄
Пример 2. Из (7.4) и интегралов 1 и 2 таблицы 2 следует, что
|
|
|
1 |
dx = |
1 |
ln ax |
+ b |
||
|
ax |
+ b |
a |
||||||
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
1 (ax + b) |
−s+1 |
||
|
|
s dx |
= |
|
|||||
(ax + b) |
a |
|
(−s +1) |
||||||
|
|
|
|
|
|||||
Пример 3. Найти интеграл x3 +  x + 2dx . x
x + 2dx . x
+C
+C
,
.
◄
Решение. Преобразовав подынтегральное выражение, воспользуемся свойствами неопределенного интеграла и формулами 1 и 2 таблицы 2. Тогда
3 |
|
|
|
|
|
1 |
||
|
x + |
x + 2 |
dx = x2 |
+ x− |
||||
|
|
|||||||
|
2 |
|||||||
|
|
|||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x3 |
|
|
|
|
|
|
|
|
|
|||
+ |
|
dx = |
|
+ 2 x + 2ln x + C . |
◄ |
||
|
|
||||||
|
x |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Найти интеграл |
|
sin |
2 |
x |
dx . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Используем формулу |
2sin |
2 |
x |
=1− cos x для преобразования |
|||||||||||||
|
|||||||||||||||||
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подынтегрального выражения. Тогда из формул 1 и 5 таблицы 2 получим |
|
||||||||||||||||
sin2 |
x |
dx = |
1 |
(1− cos x)dx = |
1 |
x − |
1 |
sin x + C |
◄ |
||||||||
|
|
|
|
||||||||||||||
2 |
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
2 |
|
|
||
Пример 5. Найти интеграл ∫ |
|
|
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
2+ + |
|
|
|
|
|
|
|||||||||||

Решение. 1) Пусть 2 − 4 < 0. Тогда, используя (7.4) и интеграл 10 из таблицы 2, получим
|
|
|
1 |
dx = |
|
x |
2 |
+ px + q |
|
||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2) Пусть 2 − 4 = 0.
2)
|
|
|
1 |
|
|
p |
2 |
||
x + |
+ |
|||
2 |
|
|||
|
|
|
||
Тогда 2
|
|
|
|
|
|
|
x + |
p |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
dx = |
|
arctg |
|
|
+ C . |
||
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|||
|
p |
|
|
p |
2 |
|
p |
2 |
|
|
q − |
|
|
q − |
|
q − |
|
|
|||
4 |
|
4 |
4 |
|
||||||
|
|
|
|
|
||||||
+ + = ( + 2)2. Очевидно, (пример
1−1
∫( +2)2 = +2 + .
3)Пусть 2 − 4 > 0. Тогда уравнение 2 + + = 0 имеет два разных
вещественных корня 1 |
и 2, подынтегральная дробь раскладывается в сумму |
|||||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
||||
|
|
= |
|
= |
|
|
|
|
( |
|
|
− |
|
|
). |
|||||||
|
2+ + |
( − )( − ) |
( − ) |
− |
1 |
− |
2 |
|||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|||
Следовательно, интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∫ |
|
1 |
|
= |
|
1 |
|
| |
− 1 |
| + . |
◄ |
|
|
||||||||
|
2+ + |
( − ) |
|
|
|
|||||||||||||||||
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
7.4. ЗАМЕНА ПЕРЕМЕННОЙ В НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Теорема. Пусть две переменные и связаны взаимно-однозначной зависимостью, т.е. известны две взаимно-обратные дифференцируемые функции = ( ) и = ( ), имеющие непрерывные производные. Тогда
∫ ( ) = ∫ ( ( )) ′( ) . |
(7.5) |
Доказательство. Продифференцируем равенство (7.5), учитывая, что в правой части
– сложная функция, зависящая от . Тогда
( ) = ( ( )) ′( ) ′( ) = ( ),
т.к. производные взаимно-обратных функций удовлетворяют условию (4.7). Следовательно, равны и неопределенные интегралы. ■
Формула (7.5) применяется, если для интеграла в правой части найдется первообразная, а именно,
∫ ( ( )) ′( ) = ( ) + .
Тогда
∫ ( ) = ( ( )) + . |
(7.6) |
Замечание. В некоторых случаях подынтегральная функция может быть представлена в виде
( ) = ( ( )) ′( ). |
(7.7) |
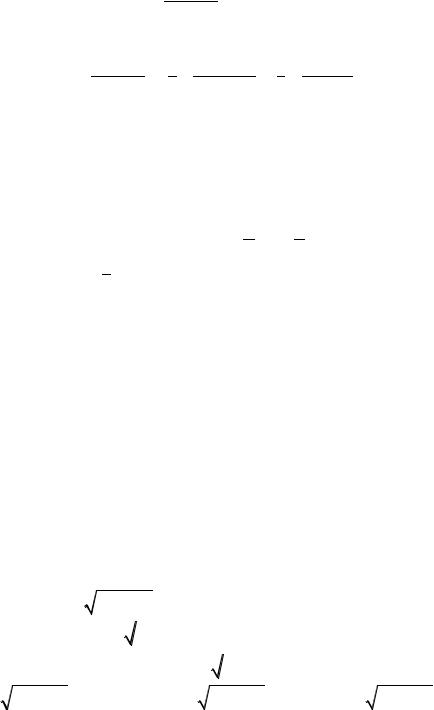
Тогда |
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
′( ) |
( |
) |
( |
) |
( ) |
( |
) |
= |
∫ ( ) = ∫ |
( ) |
= ∫ ( |
|
) ( |
|
) = ∫ |
|
|
|||
( ) + = ( ( )) + , |
|
|
|
|
|
(7.8) |
|||||
где ( ) – первообразная функции ( ).
Такой прием называется подведением под знак дифференциала.
В частности, его можно применить для доказательства (7.4).
Пример 1. Найти интеграл ∫ ( +1) .
2− +1
Решение. Используя производную знаменателя, разложим интеграл в сумму двух интегралов:
( +1) |
1 (2 −1) 3 |
|
∫2− +1 = 2 ∫ 2− +1 + 2 ∫ 2− +1.
Впервом интеграле сделаем замену: = 2 − + 1, = (2 − 1) .
Тогда (заметим, что > 0)
1 |
∫ |
(2 −1) |
= |
1 |
∫ |
|
= |
1 |
= |
1 |
ln( 2 |
− + 1) + . |
||
|
|
|
|
|
|
|
|
|||||||
2 |
2− +1 |
2 |
|
2 |
|
|||||||||
|
|
|
|
|
2 |
|
||||||||
Во втором интеграле (см. пример 5 п. 7.3) в знаменателе выделим полный квадрат
2 − + 1 = ( − 12)2 + 34
исделаем замену: = − 12 , = . Тогда
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
= √ |
|
|
|
2 |
−1 |
|
|
+ . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∫ |
= |
∫ |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2− +1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
( +1) |
|
|
|
1 |
ln( 2 − + 1) + √ |
|
|
|
2 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∫ |
= |
3 |
|
+ . ◄ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2− +1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Пример 2. Найти интеграл ∫ √ 2 − 2 , > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Используем замену: = . Тогда = . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||
∫ √ 2 − 2 = 2 ∫ 2 |
= |
|
∫(1 + 2 ) = |
|
|
( + |
2 ) + |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
== |
(arcsin ( |
) + |
|
|
2arcsin ( |
)) + = |
arcsin ( |
) + |
√ 2 |
− 2 + . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3. Найти |
|
|
|
dx |
|
|
|
|
, a 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Сделаем замену t = |
|
x2 + a2 + x, t 0 и найдем дифференциал |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
x |
2 |
+ a |
2 |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dx |
|
. |
||||||||||||||||||||||||||
|
|
dt = |
|
|
|
|
|
|
|
|
+1 dx dt = |
|
|
|
|
|
|
|
|
dx |
= |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
2 |
|
+ a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ a |
2 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
x |
2 |
+ a |
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Следовательно,

|
|
dx |
|
= |
|
dt |
= ln t + C = ln |
( |
x + |
x |
2 |
+ a |
2 |
) |
+ C . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
x |
2 |
+ a |
2 |
|
t |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замечание. Аналогичным образом (на области допустимых значений) берется интеграл
|
|
|
|
|
dx |
|
|
|
|
||
|
|
|
|
x |
2 |
+ b |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
при < 0, причем надо учитывать, что переменная |
t |
может быть меньше |
|||||||||
нуля: |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= ln x + |
x |
2 |
+ b + C . |
|
◄ |
||||
|
|
|
|
||||||||
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
||||||
|
x |
+ b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7.5. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ В НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Теорема. Пусть функции ( ) и ( ) имеют непрерывные производные
′( ) и ′( ). Тогда
∫ ( ) ′( ) = ( )( ) − ∫ ( ) ′( ) . |
(7.9) |
Формула (7.9) может быть переписана в кратком варианте через |
|
дифференциалы, а именно, |
|
∫ = − ∫ . |
(7.10) |
Доказательство также очевидно следует из дифференцирования левой и правой частей равенства (7.9). ■
Пример 1. Найти интеграл |
|
|
Решение. Обозначив u = x, dv
x cos xdx .
= cos xdx , получаем
u= x, du = dx,
x cos xdx = dv = cos xdx, v = sin x = x sin x − sin xdx = x sin x + cos x + C . ◄
Иногда приходится несколько раз применить формулу интегрирования по частям.
Пример 2. Найти интеграл
Решение. Обозначив u = ln
|
x |
2 |
x, |
|
ln |
2 |
xdx . |
|
||
dv = xdx |
||
, получаем

|
|
|
u = ln2 x, du = 2 ln x |
1 |
dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x ln2 xdx = |
|
|
|
|
|
|
|
x |
= |
x2 |
|
ln2 |
x − |
x2 |
2 ln x |
1 |
dx = |
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
dv = xdx, v = |
x |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
u = ln x, du = |
1 |
dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x2 |
|
|
|
|
|
|
x2 |
|
|
x2 |
|
|
|
x |
|
||||||||||||||
|
ln2 x − |
x ln xdx = |
x |
|
ln2 |
|
ln x − |
|||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
x2 = |
|
|
x − |
|
|
|
dx = |
||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
dv = xdx, v = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
x2 |
ln2 x − |
x2 |
ln x + |
x2 |
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 3. Найти интеграл Решение. Обозначим u = x Тогда
|
e |
x |
cos xdx . |
|
|||
|
|
||
, dv = cos xdx |
|||
◄
.
|
|
x |
|
|
|
u = e |
x |
, du = e |
x |
dx, |
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|||||||
e |
cos xdx = |
|
|
|
|
|
= e |
sin x − e |
sin xdx = |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dv |
= cos xdx, v = sin x |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
u = e |
x |
, du = e |
x |
dx, |
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|||||||
= |
|
|
|
= e |
sin x |
+ e |
cos x − e |
cos xdx. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dv = sin xdx, v |
= −cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В результате мы пришли к уравнению |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
e |
x |
cos xdx |
= e |
x |
sin x + e |
x |
cos x − e |
x |
cos xdx |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где неизвестным является исходный интеграл. Решая уравнение, одну из первообразных. Окончательно,
|
x |
|
e |
x |
sin x + e |
x |
cos x |
|
e |
cos xdx = |
|
|
+ C. |
||||
|
|
|
|
|
||||
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
Пример 4. Найти интеграл ∫ |
|
|
|
. |
|
( 2+1)2 |
||
Решение. Представим подынтегральную функцию в виде:
|
|
1 |
|
|
2+1− 2 |
|
1 |
|
|
|
2 |
|
|
||||||
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
− |
|
|
|
|
. |
( |
2 |
+1) |
2 |
( |
2 |
+1) |
2 |
|
2 |
+1 |
( |
2 |
+1) |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
получаем
◄
Интеграл от первого слагаемого – табличный, а для второго применим формулу интегрирования по частям (7.9), считая, что
|
( ) = , ′( ) = |
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
( 2+1)2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда ′( ) = 1, ( ) = |
−1 |
|
, и |
|
|
|
|
|
|
|
|
|
|
|
|
||
2( 2+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫ |
2 |
= ∫ |
|
|
= |
− |
|
+ |
1 |
∫ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
2 2 |
( |
2 |
+1) |
2 |
2 |
+1) |
2 |
2 |
|||||||||
|
( +1) |
|
|
|
|
2( |
|
|
+1 |
||||||||
Окончательно
|
|
|
|
∫ |
|
|
|
|
= |
|
|
|
+ |
1 |
∫ |
|
= |
|
|
|
+ |
1 |
+ . |
◄ |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 2 |
|
|
2 |
|
|
2 |
2 |
+1 |
2 |
+1) |
2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
( +1) |
|
|
|
2( |
+1) |
|
|
|
|
|
2( |
|
|
|
|
|
|
||||||||||||||||||||||||
Пример 5. Найти интеграл ∫ √ |
2 |
+ 2 |
, > 0. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Решение. Представим интеграл в виде суммы двух интегралов и для |
||||||||||||||||||||||||||||||||||||||||||||||||
второго применим формулу интегрирования по частям (7.9), считая, что |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( ) = , ′( ) = |
|
|
|
. Тогда ′( ) = 1, ( ) = √ 2 + 2, и |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
√ 2+ 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2+ 2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
= 2 ∫ |
|
|
|
|||||||||||||||||||||||||
∫ √ |
2 + 2 |
= ∫ |
|
|
= ∫ |
|
|
|
+ ∫ |
+ |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
√ 2+ 2 |
√ 2+ 2 |
|
√ 2+ 2 |
√ 2+ 2 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
2 + 2 |
− ∫ √ |
2 + 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Как в примере 3, получилось уравнение, где неизвестным является |
||||||||||||||||||||||||||||||||||||||||||||||||
исходный интеграл. Решив его и использовав пример 3 п.7.4, получим |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
( √ |
|
+ 2 ln( + √ |
|
)) + . |
|
|
|
|||||||||||||||||||||||||||||||||||||||
∫ √ |
2 + 2 |
= |
2 + 2 |
2 + 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
