
Оглавление |
|
2. ПРЕДЕЛ ФУНКЦИИ ................................................................................................................. |
8 |
2.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ |
|
ФУНКЦИИ............................................................................................................................................... |
8 |
2.2. ТЕОРЕМЫ О ПРЕДЕЛАХ ............................................................................................... |
10 |
2.3. ОДНОСТОРОННИЕ ПРЕДЕЛЫ...................................................................................... |
14 |
2.4. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ ...................................................................................... |
15 |
1. ОСНОВНЫЕ ПОНЯТИЯ |
|
1.1. Пусть каждому значению переменной |
из множества |
соответствует одно определенное значение другой |
переменной . |
Величина называется н е з а в и с и м о й переменной. Величина –
за в и с и м о й |
переменной. Закон, т. е. правило |
соответствия между этими |
величинами |
называется ф у н к ц и о н а л ь н о й |
з а в и с и м о с т ь ю или |
ф у н к ц и е й |
и обозначается : или = ( ). При этом независимая |
|
переменная называется аргументом , а зависимая переменная –
з н а ч е н и е м э т о й ф у н к ц и и . |
||
Множество |
возможных |
значений называется о б л а с т ь ю |
о п р е д е л е н и я |
функции и |
обозначается ( ). В данном пособии будем |
рассматривать функции вещественного аргумента, которые принимают
вещественные значения. |
Множество возможных значений называется |
|
о б л а с т ь ю и з м е н е н и я |
( о б л а с т ь ю з н а ч е н и й ) |
функции . Ее будем |
обозначать ( ). |
|
|
Графиком функции называется множество |
точек плоскости , |
|
координаты которых ( , ) связаны соотношением = ( ), где ( ). Отметим, что при таком определении мы рассматриваем о д н о з н а ч н ы е
функции, то есть любая вертикальная прямая пересекает график функции только в одной точке.
Функция может быть задана различными способами: описательно, таблично, аналитически, графически. Если функция задана одной или несколькими формулами, связывающими переменные и , то говорят, что
ф у н к ц и я з а д а н а а н а л и т и ч е с к и . Если уравнение, связывающее переменные и , разрешено относительно переменной , то говорят о я в н о з а д а н н о й функции. Если связь между переменными и записана в виде уравнения F( x, y) = 0 , не разрешенного относительно переменной , то говорят, что функция задана н е я в н о .
Зависимость функции от аргумента может осуществляться через посредство третьей переменной t , называемой п а р а м е т р о м . В этом случае говорят, что функция задана п а р а м е т р и ч е с к и .
В дальнейших пунктах опишем свойства функций, заданных аналитически и отражение этих свойств на графиках функций.
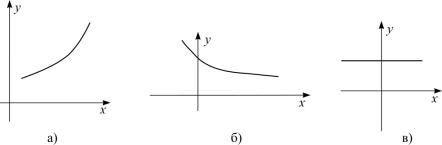
1.2. Функция называется в о з р а с т а ю щ е й на интервале ( ; ), если бóльшим значениям аргумента соответствуют бóльшие значения функции
(рис. 1,a), т. е. для любых 1, 2 ( ; ), |
таких что 1 < 2 |
выполняется |
неравенство |
|
|
(1) < (2) |
(1.1) |
|
Функция называется у б ы в а ю щ е й |
на интервале ( ; ), если бóльшим |
|
значениям аргумента соответствуют меньшие значения функции (рис. 1,б), т. е. для любых 1, 2 ( ; ), таких что 1 < 2 выполняется неравенство
(1) > (2) . |
(1.2) |
Убывающая или возрастающая функция называется монотонной. |
|
Функция, сохраняющая значение на интервале ( ; ), называется на этом интервале п о с т о я н н о й (const). Ее график – прямая, параллельная оси
(рис. 1,в).
Если в неравенствах (1.1)–(1.2) возможен и знак равенства: (1) ≤ (2) или (1) ≥ (2) то функция называется соответственно н е у б ы в а ю щ е й
или н е в о з р а с т а ю щ е й .
Рис. 1 Функция называется о г р а н и ч е н н о й на интервале ( ; ), если на этом
интервале выполняется неравенство |
|
||
|
|
|( )| ≤ , |
(1.3) |
где постоянная > 0. Если на интервале ( ; ) выполняется неравенство |
|||
|
|
( ) ≤ ( ( ) ≥ ), |
(1.4) |
где – какая-то |
постоянная, то функция называется о г р а н и ч е н н о й |
||
с в е р х у |
( с н и з у ) |
постоянной на этом интервале. |
|
1.3. |
Функция |
называется ч е т н о й , если область |
ее определения |
симметрична относительно нуля и для любого значения ( ) справедливо равенство (− ) = ( ). График четной функции имеет ось симметрии – ось
.
Функция называется н е ч е т н о й , если область ее определения симметрична относительно нуля и для любого значения ( ) справедливо равенство (− ) = − ( ). График нечетной функции имеет центр симметрии
– точку (0, 0). Примеры графиков четной и нечетной функций представлены на рис. 2 (рис. 2,a – четная, рис. 2,б – нечетная).

Рис. 2
1.4. Функция называется п е р и о д и ч е с к о й , если существует такое число ≠ 0, что для всех допустимых значений справедливо равенство
|
( + ) = ( ). |
(1.5) |
При этом п е р и о д о м |
функции называется |
наименьшее |
положительное число 0, для которого верно равенство (1.5). Примеры графиков таких функций представлены на рис. 3.
Рис. 3
1.5. Функция называется с л о ж н о й (с у п е р п о з и ц и е й двух функций), если ее аргумент сам является функцией. Обозначение: = ( ( )). Область определения «внешней» (последней по порядку действия) функции ( ). должна содержать область значений «внутренней» = ( ). Это определение распространяется на любое конечное число функций.
1.6. Пусть на множестве
D
задана монотонная функция
y =
f
( x)
,
имеющая множество значений |
E . Тогда между двумя переменными и |
существует взаимно-однозначное соответствие, то есть каждому значению одной переменной соответствует одно и только одно значение другой. В этом
случае существует и функция |
x = |
f |
−1 |
(y)( f −1 – обозначение функции), |
|
которая называется обратной к функции y = f ( x) . Графиком этих функций является одна кривая. Если у функции x = f −1 (y) , как привычно, обозначить
аргумент буквой x , а значение функцию
y =
функции
f |
−1 |
( x), x |
|
–
E
буквой y , то получим новую
, y D ,
которую тоже называют обратной к функции = ( ), что не вызывает
затруднений, так как функция ( f ( y = f ( x))) и такой обратной ( y
−1
=
) – это закон соответствия. Графики прямой f −1( x), x E, y D ) функций симметричны
относительно прямой y = x . Очевидно, функция f является обратной к

функции |
f |
−1 |
, поэтому две функции |
f |
и f |
−1 |
называются в з а и м н о - |
|
|
о б р а т н ы м и .
Примеры.
1) На рисунке 4 представлены графики показательной и логарифмической функций, которые взаимно-обратны.
2) Функция
2 |
, x R |
y = x |
Рис.4 не монотонная и не имеет обратной. Но каждая
из функций:
2 |
, x 0;+ ) |
y = x |
и
y = x |
2 |
, x (−;0 |
|
– монотонна в области
своего задания и имеет обратную, соответственно,
5).
y = |
x |
и
y
= − |
x |
(см. рис.
а) |
б) |
Рис. 5
3) Рассмотрим функцию случае одному значению
множество значений |
x D( f ) |
y = cos x, D( f ) : (− ; + ), E( f ) : −1;1 . |
В этом |
|
y E( f ) : −1;1 |
соответствует бесконечное |
|
. Однако на промежутке 0; y = cos x |
строго |
|
убывает и принимает все значения от 1до –1, и, значит, на нем имеет обратную= arccos . Обе функции изображены на рисунке 6.

Рис. 6
1.7.Прямая, проходящая хотя бы через две точки кривой, называется
секущей . Пусть секущая проходит через точки и 1 (рис. 7, прямая 1), причем точка – неподвижная точка на кривой, а точка 1 перемещается по кривой, приближаясь к точке . Прямая, которая займет предельное
положение секущей 1 называется к а с а т е л ь н о й к к р и в о й в т о ч к е(рис. 7, прямая 2).
Рис. 7
Кривая, имеющая касательную, которая непрерывно меняется от точки к точке, называется г л а д к о й .
1.8. Кривая называется в ы п у к л о й , если любая секущая пересекает ее только в двух точках.
Понятие выпуклости переносится на график функции и, тем самым, на саму функцию. Но так как график функции имеет ориентацию относительно системы координат, то для него различают следующие два случая.
Если все точки графика функции на промежутке ( ; ) лежат выше любой касательной, то функция называется в ы п у к л о й в н и з и л и в о г н у т о й на промежутке ( ; ) (рис. 8,a).
Если все точки графика функции на промежутке ( ; ) лежат ниже любой касательной, то функция называется в ы п у к л о й в в е р х и л и в ы п у к л о й на этом промежутке (рис. 8,б).

Рис. 8 Точка 0 называется точкой п е р е г и б а , если в этой точке функция
меняет тип выпуклости (рис. 9)
|
Рис.9 |
|
|
|
|
1.9. Функция |
имеет м а к с и м у м |
( м и н и м у м ) |
в |
точке 0, если |
|
существует такая |
окрестность этой |
точки ( ) = ( − δ; + δ), |
|||
|
|
|
0 |
0 |
0 |
принадлежащая области определения функции, что для всех |
( ), ≠ |
||||
|
|
|
|
|
0 |
0, выполнено неравенство |
|
|
|
|
|
|
( ) < (0) |
( ( ) > (0)). |
|
(1.6) |
|
Для обозначения максимума или минимума существует объединяющий |
|||||
их термин – э к с т р е м у м . Точка 0 называется т о ч к о й |
э к с т р е м у м а |
||||
(точкой максимума или минимума). Примеры функций, имеющих экстремум, приведены на рис. 10.
Рис. 10
1.10. Неограниченная кривая может иметь асимптоты. А с и м п т о т о й кривой называется прямая линия такая, что если двигаться по кривой, то расстояние от кривой до прямой (асимптоты) стремится к нулю.
Для графиков различают в е р т и к а л ь н ы е и н е в е р т и к а л ь н ы е
асимптоты, т.к. уравнения этих прямых имеют различный вид. Ниже приведены примеры асимптот: вертикальная: = 0 (рис. 11,а), наклонная:= + (рис. 11,б), горизонтальная (частный случай наклонной): =
(рис. 11,в).

|
Рис. 11 |
|
1.11. |
Среди множества функций, заданных аналитически, выделяют |
|
функции, |
которые называются о с н о в н ы м и |
э л е м е н т а р н ы м и |
ф у н к ц и я м и :
показательная
постоянная
y = a |
x |
(a 0,a |
|
y = 1);
c , c |
– константа; |
|
логарифмическая |
y |
|
степенная
= log |
a |
x (a |
|
|
y = x |
α |
|
|
0,a 1) |
|
;
;
тригонометрические
тригонометрические
y = sin y = arcsin x ,
x, y
y =
= cos x, y = tgx, y =
arc cos x, y = arctgx,
ctgx ;
y = arcctgx
обратные
.
Э л е м е н т а р н ы м и ф у н к ц и я м и называются те, которые могут быть получены из основных элементарных функций при помощи арифметических действий, сложные функции, построенные из них и обратные к ним.
Примерами элементарных функций являются:
м н о г о ч л е н ы ( п о л и н о м ы ) –
где
an
0
,
|
|
i=n |
y = Pn (x) = a0 + a1x + a2 x2 |
+ ...an xn = ai xi , |
|
|
|
i=0 |
при этом число n |
называется с т е п е н ь ю м н о г о ч л е н а , |
|
(многочлен первой степени называется л и н е й н о й ф у н к ц и е й , второй степени – к в а д р а т и ч н о й );
р а ц и о н а л ь н ы е ф у н к ц и и ( р а ц и о н а л ь н ы е д р о б и ) :
y = Pn ((x))
где Pn (x), Qm (x) – многочлены;
Qm x ,
и р р а ц и о н а л ь н ы е ф у н к ц и и (иррациональной функцией называется функция, которая задана с помощью суперпозиций рациональных функций, степеней с рациональными показателями и четырех арифметических
действий, например,
y= 3 x2 +
x2 + 
 x x2 +1
x x2 +1
).
Если функция задана разными условиями на разных промежутках, то она
не элементарна. |
|
|
|
|
x, x |
( |
−;1 , |
||
|
|
|
) |
|
1 |
|
|
|
|
|
, x −1;2), |
|||
Пример. Построить график функции y = |
|
|||
|
||||
x |
|
|
|
|
2, x 2; + )

Решение. Функция строится из элементарных функций, заданных на определенных промежутках, где и построим графики этих функций. Символ «°» означает, что соответствующая точка не принадлежит графику. Окончательно получим график, изображенный на рис. 12.
Рис. 12
2.ПРЕДЕЛ ФУНКЦИИ
2.1.ОПРЕДЕЛЕНИЕ ПРЕДЕЛА. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО
БОЛЬШИЕ ФУНКЦИИ
Пусть функция = ( ) определена в некоторой окрестности точки 0,
исключая, может быть, саму эту точку. |
|
|
Число называется п р е д е л о м функции ( ) при |
x , стремящемся к |
x0 |
(обозначение → 0) если для любого сколь угодно малого > 0 существует такое число > 0, что для всех значений , удовлетворяющих неравенствам
0 < | − 0| < , |
(2.1) |
выполнено неравенство
| ( ) − | < .
Обозначение:
lim ( ) = или
→0
(2.2)
f ( x) |
→ |
A . |
|
x→x |
|
|
0 |
|
Теорема 1. Если у функции ( ) существовует предел lim ( ) = , то
→0
в окрестности ( 0) функция ( ) – ограничена, причем для ( 0) | ( )| < | | + .
Доказательство следует из свойств модуля и неравенств (2.1) и (2.2).
Если число = 0, то функция ( ) называется б е с к о н е ч н о м а л о й
при → 0.
Теорема 2. Для того, чтобы существовал предел lim ( ) =
→0
необходимо и достаточно, чтобы ( ) = ( ) − была бесконечно малой при
→ 0.
Доказательство очевидно следует из определения бесконечно малой и подстановки функции ( ) = ( ) − в неравенство (2.2). ◄
Выше приведены определения для конечных значений и 0. Они могут быть переписаны для случаев, когда или 0 обращаются в бесконечность

(∞). Символ ∞ используется для обозначения б е с к о н е ч н о б о л ь ш о й функции (или переменной) при → 0. При этом соответствующие неравенства в определении предела должны быть заменены на неравенства типа | | > , если → ∞, > , если → +∞, < − , если → −∞, и т.п.
Например, символ
lim ( ) = −∞
→+∞
означает, что для любого сколь угодно большого числа > 0 существует число > 0 такое, что из неравенства > следует ( ) < − . Остальные подобные определения рекомендуем написать самостоятельно.
Связь между бесконечно большими и бесконечно малыми показывает
Теорема 3. Для того, чтобы функция ( ) была бесконечно большой при→ 0 необходимо и достаточно, чтобы ( ) = (1) была бесконечно малой
при → 0.
Доказательство проводится в два этапа.
Пусть сперва ( ) = (1) - бесконечно малая при → 0. Зададим число
> 0. По нему построим = 1. Так как ( ) - бесконечно малая, существует такое > 0, что для всех значений , удовлетворяющих неравенствам 0 <
| − 0| < , выполнено неравенство | ( )| < . То есть |(1)| < 1, что эквивалентно неравенству | ( )| > . Последнее означает, что ( ) - бесконечно большая.
Пусть теперь ( ) - бесконечно большая при → 0. Зададим число > 0. По нему построим = 1. Так как ( ) - бесконечно большая, существует такое > 0, что для всех значений , удовлетворяющих неравенствам 0 <
| − | < , выполнено неравенство | ( )| > . Тогда | ( )| = | |
1 |
| < |
1 |
= |
|||
|
|
||||||
0 |
|
|
|
() |
|
|
|
|
|
|
|
|
|||
, то есть ( ) - бесконечно малая. ◄ |
|
|
|
|
|
||
Подобным |
же |
образом |
определяется |
п р е д е л |
|||
п о с л е д о в а т е л ь н о с т и . |
А именно, последовательность занумерованных |
||||||
чисел , , где - множество натуральных чисел, можно рассматривать как функцию натурального аргумента: = ( ). Тогда число называется
п р е д е л о м п о с л е д о в а т е л ь н о с т и при → ∞, если для любого сколь угодно малого числа > 0 существует номер такой, что при всех номерах
> выполняется неравенство | − | < . Поэтому все в дальнейшем сформулированные утверждения о пределах функций верны и для последовательностей.
Пример. Пусть ( ) = , ( ) = (−∞; +∞). Тогда для любого 0 |
|
lim = 0. |
(2.3) |
→0 |
|

Доказательство. Очевидно, что в этом случае неравенства (2.1) и (2.2) совпадают при = . ◄
Для отыскания пределов в случае более сложных функций следует использовать свойства пределов и теорему о непрерывности элементарных функций.
2.2. ТЕОРЕМЫ О ПРЕДЕЛАХ
Для бесконечно малых верны следующие леммы, на которые опирается доказательство теорем о пределах.
Лемма 1. Пусть ( ) и ( ) - бесконечно малые при → 0. Тогда их сумма ( ) = ( ) + ( ) – тоже бесконечно малая при → 0.
Доказательство. Зададим число > 0. По нему построим 1 = 2 = 2.
Так как ( ) - бесконечно малая, то существует такое число 1 > 0, что для всех , удовлетворяющих неравенству 0 < | − 0| < 1, выполнено неравенство
| ( )| < 1. |
(2.4) |
Аналогично для ( ) существует такое число 2 > 0, что для всех , |
|
удовлетворяющих неравенству 0 < | − 0| < 2, выполнено неравенство |
|
| ( )| < 2. |
(2.5) |
Возьмем = min { 1, 2}. Тогда для всех , удовлетворяющих |
|
неравенству 0 < | − 0| < , выполнены оба неравенства (2.4) и (2.5) и, |
|
следовательно, |
|
| ( ) | = | ( ) + ( )| ≤ | ( )| + | ( )| < 1 + 2 = . |
◄ |
Лемма 2. Пусть ( ) – бесконечно малая при → 0, а функция ( ) – ограниченная в окрестности точки 0. Тогда произведение ( ) = ( ) ( ) – бесконечно малая при → 0.
Доказательство аналогично. (Советуем его провести в качестве упражнения). ◄
Следствие 1. Произведение бесконечно малой на постоянную есть бесконечно малая.
Следствие 2. Произведение двух бесконечно малых - тоже бесконечно малая.
Пусть существуют пределы lim ( ) = , lim ( ) = , причем и –
→ 0 → 0
конечные числа, 0 – любое конечное число или бесконечность. Сформулируем несколько теорем, которые описывают свойства пределов.
Теорема о пределе постоянной.
Пусть = ( ) = = , ( ) = (−∞; +∞). Тогда для любого 0
пределом постоянной является эта же постоянная, то есть
