

|
|
31 |
Угол – это "острый угол" между направляющим вектором прямой и |
||
нормалью к плоскости . |
Нормаль к плоскости N = (6;−1;2) , направляющий |
|
вектор прямой |
s = (4;0;1) |
. Окончательно из формулы (17) получаем |
|
||
|
|
|
( |
) |
|
|
26 |
|
||
sin = |
6 4 + |
|
−1 |
0 + 2 1 |
= |
|
|
|
||
36 |
+1 + 4 |
16 + 0 +1 |
41 |
|
17 |
|||||
|
|
|||||||||
0,984
,
1,396 радиан или, переводя в градусную Пример 31. Написать уравнение плоскости, параллельные прямые:
меру, 80 . |
◄ |
проходящей |
через две |
|
|
|
|
l |
: |
3x + 2 y + 3z + 4 |
= 0, |
|
|
||
1 |
|
|
|
|
|
4x + 4 y + 5z + 6 |
= 0 |
и
l |
|
: |
x −1 |
= |
y + 2 |
= |
z − 2 |
. |
|
2 |
2 |
3 |
−4 |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
Решение. Через две параллельные прямые можно провести плоскость, и при том только одну. Для этого можно взять две точки на одной прямой, одну на
другой и записать уравнение плоскости, проходящей через три точки (29). |
||||||||
Параллельность прямых доказана в примере 23. Выбрав три точки: |
||||||||
A(0,1, −2) l1; |
B (1, −2, 2) l2 |
; |
C (−1, −5,6) l2 |
, |
||||
запишем уравнение плоскости, проходящей через три точки |
|
|||||||
x |
y −1 |
z + 2 |
|
|
|
|||
1 |
−3 |
|
4 |
= 0, |
|
|||
−1 |
−6 |
( |
8 |
|
) |
|
|
|
|
( |
) |
|
|
|
|
||
−12 |
|
y −1 − 9 |
|
z + |
2 |
|
= 0, |
|
|
|
4 y + 3z + 2 = 0. |
◄ |
|||||
|
|
|
|
|
|
|
|
|
Пример 32. Написать уравнение плоскости, проходящей через пересекающиеся прямые:
l |
: |
x − y + 2z − 7 = 0, |
|
|
|||
1 |
|
||
|
|
2x + y − z = 0 |
x + 2 y + z − 9 = 0,
иl2 : 3x + y + z − 9 = 0.
Решение. В примере 24 показано, что заданные прямые пересекаются. Через пересекающиеся прямые можно провести плоскость, и при том только одну. Сведем решение к решению примера 13. Направляющие векторы прямых, параллельные искомой плоскости, найдены в примере 24. Точку, принадлежащую плоскости, можно взять на любой прямой, в том числе и точку пересечения (пример 24). Получаем
x −1 |
y − 2 |
z − 4 |
|
−1 |
5 |
3 |
= 0, |
1 |
2 |
−5 |
|
( |
) |
|
( |
|
) |
|
( |
|
) |
|
−31 x −1 |
− 2 |
|
y − 2 |
|
− 7 |
|
z − 4 |
|
= 0, |
|
|
−31x − 2 y − 7z + 63 = 0. |
◄ |
||||||||
Решить пример можно и другим способом. Надо взять на одной прямой две точки, на другой одну точку и записать уравнение плоскости, проходящей через три точки (29). Рекомендуем это проделать самостоятельно и сравнить ответы.

32
Пример 33. Написать уравнения
которых проходит через прямую l1 :
а другая – через прямую |
l2 |
: |
x − |
|
2 |
||||
|
|
|
двух параллельных плоскостей, одна из
|
3x + 2 y + 3z + 4 = 0, |
||||
|
|
|
|
|
|
4x + 4 y + 5z + 6 = 0, |
|||||
1 |
= |
y − 3 |
= |
z + 2 |
. |
|
−1 |
1 |
|||
|
|
|
|
||
Решение. Заданные прямые являются скрещивающимися (пример 27). Следовательно, существует единственная пара параллельных плоскостей, в которых лежат эти прямые. Направляющие векторы прямых параллельны каждой из плоскостей. Вектор нормали к плоскостям N = (1;10;8). Осталось на
каждой прямой взять по точке и воспользоваться формулой (27). Возьмем точку A(0,1, −2) l1 , получим уравнение первой плоскости:
x+10( y −1) + 8(z + 2) = 0,
x+10 y + 8z + 6 = 0.
Взяв точку B (1,3, −2) l2 |
, аналогично получаем уравнение для другой |
плоскости |
|
|
|
|
|
|
|
|
|
|
x +10 y + 8z + 45 = 0. |
|
◄ |
|
|
|
|
|
|
|
Пример 34. Найти |
точку |
M симметричную точке |
P(1,3, −4) |
относительно |
||
плоскости |
3x + y − 2z = 0 |
. |
|
|
|
|
|
|
|
|
|
||
Решение. Две точки симметричны относительно плоскости, если они лежат на одной прямой, перпендикулярной плоскости, и находятся на одинаковом расстоянии от плоскости. Нормаль к плоскости является направляющим вектором прямой, перпендикулярной плоскости. Уравнения
x = 3t +1, |
y = t + 3, |
z = −2t − 4 |
, |
|
|
|
задают прямую, перпендикулярную плоскости, и проходящую через точку
|
P(1,3, −4) . Найдем значение параметра для точки |
O – точки пересечения этой |
||||||||||||||||
прямой с плоскостью: |
( |
|
) |
|
( |
|
|
) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
3 |
|
3t +1 + t + 3 − 2 |
|
−2t − |
4 |
|
= 0, |
|
|
|||
|
|
|
|
|
|
|
|
|
14t = −14, |
t = −1. |
|
|
|
|
|
|
||
|
|
|
Для точки P(1,3, −4) |
значение параметра |
t |
= 0 |
. Так как точки |
P и |
M |
|||||||||
находятся на одинаковом расстоянии от точки O , то для искомой точки |
M |
|||||||||||||||||
Значение параметра |
t = −2 |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Откуда находим координаты искомой точки: M (−5,1,0). |
|
◄ |
|||||||||||||
Пример 35. Проверить, |
|
что точка |
|
|
A(2,5, −6) |
не лежит на |
прямой |
|||||||||||
|
x −1 |
= |
y +1 |
= z + 3. Написать уравнение плоскости, |
какой принадлежат эти |
|||||||||||||
|
|
|
|
|||||||||||||||
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
прямая и точка.

Решение.
получаем
33
Подставляя координаты заданной точки в уравнения прямой,
2 −1 |
|
5 +1 |
. Следовательно, точка |
A(2,5, −6) |
не лежит на прямой. По |
|
2 |
3 |
|||||
|
|
|
|
аксиоме стереометрии через прямую и точку, не лежащую на прямой, можно провести плоскость и только одну (рис. 19).
В. .А
.А
Рис. 19
Возьмем на прямой точку B(1, −1, −3) и, соединив ее с точкой A(2,5, −6) ,
получим вектор BA = (1;6;−3). Направляющий вектор прямой s = (2;3;1) Векторы BA, s параллельны плоскости. По формуле (30) записываем
.
x − 2 |
y − 5 |
1 |
6 |
2 |
3 |
z + 6 |
|
−3 |
= |
1 |
|
0
.
Вычисляя определитель, окончательно получаем |
|
−15x + 7 y + 9z + 49 = 0. |
◄ |
|
Другой вариант решения задачи: взять на прямой две точки и воспользоваться формулой 29. Рекомендуем читателям проделать вычисления самостоятельно.
2.4 Кривые на плоскости и в пространстве
Одним из удобных способов описания кривой ( l ) в трехмерном пространстве является задание трех уравнений вида
x = x(t), y = y(t), z = z(t), t ,
(36)
где каждому значению переменной t соответствует одна и только одна точка кривой (l), причем ( x(t), y(t), z(t) ) – координаты этой точки. Переменная t
называется параметром, а уравнения (36) – параметрическим заданием кривой (l).
Кривая (l) называется гладкой , если функции x(t), y(t), z(t) имеют непрерывные производные x '(t), y '(t) и z '(t).
Если на кривой задано направление , то она называется путем . В уравнениях (36) направление можно связать, например, с возрастанием параметра t.

|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
Как известно (см., например, [1]), |
касательная в |
точке с |
||||||||||
координатами ( x0 , y0 , z0 ) к кривой , |
заданной в виде (36), |
описывается |
|||||||||||
уравнениями прямой в канонической форме |
|
|
|
|
|
||||||||
|
x − x |
= |
y − y |
= |
z − z |
|
, |
|
|||||
|
|
|
0 |
|
|
0 |
|
|
0 |
(37) |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
x '(t |
|
) |
|
y '(t |
|
) |
|
z '(t |
|
) |
|
|
|
0 |
|
0 |
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
где |
x0 = x(t0 ), y0 = y(t0 ), z0 = z(t0 ) , |
при этом хоть одно из чисел, стоящих в |
|||||||||||
знаменателях уравнений (37), не должно равняться нулю.
Пример 36. Найти канонические уравнения касательной к винтовой линии
(рис. 19) |
x = a cost, y = a sin t, z = ct, (a 0, c 0), |
в точке M |
0 |
(0, a, c ). |
|
|
|
2 |
|
|
|
|
|
Рис. 20 Рис. 21
Решение. На рис. 19 нарисован один виток винтовой линии, соответствующий
изменения параметра t от 0 до 2 . Точке M 0 |
соответствует значение |
t = |
|
. |
|||||||||||||||
2 |
|||||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Производные x '(t) = −a sin t, y '(t) = a cost, z '(t) = c , при этом x ' |
|
|
= −a, |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
y ' |
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда уравнения касательной |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
= |
y − a |
= |
z − c |
. |
|
|
|
|
◄ |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
−a |
|
0 |
|
|
|
c |
|
|
|
|
|
|
||||
|
|
Для кривой, лежащей в плоскости x0y, в уравнениях (36) |
z = 0. |
|
|
||||||||||||||
Уравнение касательной (37) в этом случае |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x − x0 |
= |
y − y0 |
. |
|
|
|
|
(38) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x '(t0 ) |
|
y '(t0 ) |
|
|
|
|
|
|
||||||
Приведем несколько примеров таких кривых.
Окружность радиуса R с центром в точке описывается уравнением
M |
(x |
, y |
) |
0 |
0 |
0 |
|
(рис. 21)
(x − x0 )2 + ( y − y0 )2 = R2.
35
За параметр t удобно взять угол из полярной системы координат, если
полюс совпадает с точкой |
M |
0 |
, а полярная ось параллельна положительной |
|
полуоси X. Тогда уравнения (36)
x = x0 + R cost, y = y0 + R sin t, 0 t 2 .
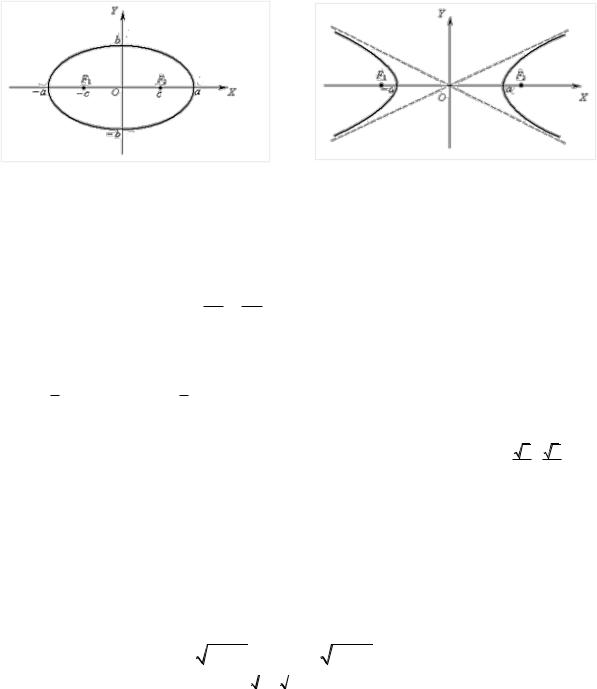
Известно (см. [1]), что каноническое уравнение эллипса (рис. 22) с
центром симметрии в начале координат имеет вид
x2 |
|
y2 |
(39) |
|
|
+ |
|
=1, (a 0, b 0). |
|
a2 |
b2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 23 |
|
|
|
|
|||||
|
|
|
Следовательно, параметрическое описание эллипса имеет вид |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = a cost, |
|
y = bsin t, 0 t 2 . |
|
|
|
|
|||||||||||||||||||
|
|
|
Аналогично для гиперболы (рис. 22) (см. [1]) каноническое |
||||||||||||||||||||||||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
=1, (a 0, b 0). |
|
|
|
(40) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
b |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
В качестве параметрических уравнений (36) можно взять |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = acht, |
|
y = bsht, − t + . |
|
|
|
|
|||||||||||||||||||
где |
cht = |
1 |
(e |
t |
+ e |
−t |
), sht = |
1 |
(e |
t |
− e |
−t |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример |
|
|
|
37. |
Для |
лемнискаты |
|
|
|
Бернулли (x2 + y2 )2 = 2xy |
|
написать |
|||||||||||||||||||||||||||||
параметрические уравнения (36) и найти касательную в точке M0 ( |
2 |
, |
2 |
). |
|||||||||||||||||||||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
Используя формулы |
|
x = r cos , |
y = r sin , перепишем уравнение |
|||||||||||||||||||||||||||||||||||
(x |
2 |
+ y |
2 |
) |
2 |
|
= 2xy |
в полярных координатах. Получим |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
2 |
= sin 2 . |
|
|
|
(41) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Кривая |
(рис. |
24) |
существует, если sin 2 0. Это означает, что |
|||||||||||||||||||||||||||||||||||
|
|
0; |
|
|
|
|
|
3 |
|
. |
Возьмем за параметр t угол , т.е. t = . Тогда, учитывая |
||||||||||||||||||||||||||||||
|
2 |
|
; |
2 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(41), уравнения (36) примут вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
sin 2t cost, y = |
sin 2t sin t. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
) соответствует t0 = 4 . |
|
|
|
|
||||||||||||||||||||||
|
|
|
Точке M 0 |
|
с координатами |
|
|
2 |
, |
|
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
||||||||||||||||||||||||||||||
Производные

36
x '(t) = |
cos3t |
, y '(t) = |
sin 3t |
, x '( |
|
)= − |
2 |
, y '( |
|
)= |
2 |
. |
|
sin 2t |
sin 2t |
4 |
2 |
4 |
2 |
||||||||
|
|
|
|
|
|
|
Следовательно, уравнение касательной
x − |
2 |
|
y − |
2 |
|
|
2 |
= |
2 |
. |
|||
|
|
|||||
|
|
|
|
|||
− |
2 |
|
2 |
|
|
|
2 |
|
2 |
|
|
||
|
|
|
|
Рис. 24 После преобразований окончательно получаем
x + y = |
2. |
◄
Если плоская кривая является графиком |
однозначной функции |
||
y = f (x), a x b, |
или графиком однозначной функции |
x = g( y), c y d, |
|
|
|
||
то в качестве параметра можно взять |
t = x |
или |
t = y, |
соответственно. |
||||
|
|
|
||||||
Уравнение (38) касательной в точке с координатами (x0 , y0 ) в этом |
||||||||
случае имеет вид: |
|
|
|
|
|
|
|
|
x − x |
= |
y − y |
, |
y |
= f (x ), |
|
||
0 |
|
0 |
|
|||||
1 |
|
f '(x ) |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
x − x |
= |
y − y |
, x |
= g( y ), |
|
|||
0 |
|
0 |
|
|||||
g '( y ) |
|
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
соответственно, что приводит к стандартному уравнению y = y0 + f '(x0 )(x − x0 ),
или
Пример 38. Для
уравнением |
y |
2 |
|
x = x0 + g '( y0 )( y − y0 ).
параболы (рис. 25), заданной (см. [1]) каноническим
= 2 px, p 0 , найти касательную в точке с координатами
(x0 , y0 ) , где
|
|
y |
2 |
|
x |
= |
0 . |
||
|
||||
0 |
|
2 p |
||
|
|
|||

37
|
|
|
|
|
|
y |
2 |
|
|
Решение. Данная парабола является графиком однозначной функции |
x = |
|
. |
||||||
2 p |
|||||||||
|
|
||||||||
|
|
|
|
|
|
|
|||
|
y |
|
y |
|
|
|
|
|
|
Производная x ' = |
|
, x '( y0 ) = |
0 |
. Следовательно, уравнение касательной |
|
|
|
||
p |
p |
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
y |
|
|
|
y |
2 |
|
y |
y |
|
y |
2 |
|
y |
y |
|
y |
2 |
|
y |
|
|
x = x |
+ |
( y − y |
|
) = |
|
+ |
− |
|
= |
− |
|
= |
|
). |
|||||||||
0 |
o |
|
0 |
0 |
|
|
0 |
0 |
|
|
0 |
0 (2 y − y |
0 |
||||||||||
0 |
|
p |
|
|
2 p |
|
p |
|
p |
|
p |
|
2 p |
|
2 p |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рис. 25 |
|
|
|
||
Окончательно, |
|
|
|
|
|
2 px = 2 y |
|
y − y |
|
2 |
. |
0 |
0 |
|
|||
|
|
|
|
||
◄
2.5Поверхности второго порядка
Втрехмерном пространстве с декартовой системой координат
уравнение поверхности может быть задано в явной форме в неявной форме
F = (x, y, z) = 0.
z =
f (x, y)
или
(42)
Если в уравнении (42) хоть одна из переменных x, y или z входит в квадрате (или две переменные перемножаются), то такая поверхность называется поверхностью второго порядка (точное определение см. [1]). Опишем несколько различных видов таких поверхностей.
Сферой радиуса R с центром в точке
M |
0 |
(x |
, y |
, z |
0 |
) |
|
0 |
0 |
|
|
называется
поверхность, образованная точками, удаленными на расстояние R от центра.
Из формулы для расстояния между точками M0 (x0 , y0 , z0 ) получается уравнение сферы (рис. 25):
и |
M |
|
(x, y, z)
(x − x0 )2 + ( y − y0 )2 + (z − z0 )2 = R2.
На рис. 26 x0 = y0 = z0 = 0.

38
Рис. 26 |
|
|
Эллипсоид с полуосями |
a, b, c |
(a 0, b 0, c |
координат (рис. 27) описывается уравнением
Рис.
0)
27
и центром в начале
x |
2 |
|
y |
2 |
|
z |
2 |
|
|
|
+ |
|
+ |
|
=1. |
||||
a |
2 |
b |
2 |
c |
2 |
||||
|
|
|
|||||||
|
|
|
|
|
|
Если совпадают два параметра из трех, например,
a = b,
то уравнение
x |
2 |
|
y |
2 |
|
z |
|
|
+ |
|
+ |
||||
a |
2 |
a |
2 |
c |
|||
|
|
||||||
|
|
|
|
2 2
=1
описывает эллипсоид вращения (в данном случае вокруг оси Z).
Если a = b = c = R , то эллипсоид превращается в сферу радиуса R (рис.
26).
Эллиптический параболоид (рис. 28) описывается уравнением
|
x |
2 |
|
y |
2 |
|
|
z = |
|
+ |
|
, (a 0, b 0). |
|||
a |
2 |
b |
2 |
||||
|
|
|
|||||
|
|
|
|
|
Рис. 28 |
|
|
Рис. 29 |
|
Сечение горизонтальными плоскостями – эллипсы, сечения |
||||
вертикальными плоскостями – параболы. |
||||
Если a = b, то параболоид называется параболоидом вращения |
||||
(вокруг оси Z). |
|
|
|
|
Уравнение |
|
|
|
|
z2 = |
x2 |
+ |
y2 |
, (a 0, b 0), |
a2 |
|
|||
|
|
b2 |
||
описывает конус (рис. 29).

39
Горизонтальные сечения – эллипсы, вертикальные сечения – гиперболы,
а сечения плоскостями
x = 0
и
y = 0
– прямые
z = |
y |
|
b |
||
|
и |
z |
= |
x |
, |
|
|
|
|
a |
|
соответственно. Уравнение
|
y |
2 |
|
x |
2 |
|
|
z = |
|
− |
|
, (a 0, b 0), |
|||
b |
2 |
a |
2 |
||||
|
|
|
|||||
|
|
|
|
|
описывает гиперболический параболоид (рис. 30).4
Горизонтальные сечения параболы, а сечения плоскостью
Рис. 30
– гиперболы,
z = 0 |
– прямые |
|
вертикальные сечения –
y = |
b |
x. |
|
|
|
|
a |
|
Уравнение
x |
2 |
|
y |
2 |
|
z |
2 |
|
|
|
+ |
|
− |
|
=1, (a 0, b 0, c 0), |
||||
a |
2 |
b |
2 |
c |
2 |
||||
|
|
|
|||||||
|
|
|
|
|
|
описывает однополостной гиперболоид (рис. 31).
(43)
Рис. 31 Рис. 32 Горизонтальные сечения – эллипсы, вертикальные сечения – гиперболы. Уравнение
x2 |
+ |
y2 |
− |
z2 |
= −1, (a 0, b 0, c 0), |
(44) |
a2 |
b2 |
c2 |
4 Аналогичные поверхности (по-другому ориентированные относительно осей координат)
описывают и уравнения: z = axy, (a 0); z = x2 − y2 , (a 0, b 0). a2 b2

40
описывает двуполостной гиперболоид (рис. 32). Здесь тоже горизонтальные сечения – эллипсы, а вертикальные сечения – гиперболы.
Замечание. Другое распределение знаков в уравнениях (43), (44) меняет ориентацию поверхности относительно осей координат.
Если в уравнение поверхности не входит одна из трех переменных x, y или z, то поверхность называется цилиндрической , и соответствующая координатная ось параллельна этой поверхности.
Например, уравнение
x |
2 |
|
y |
2 |
|
|
|
+ |
|
=1, (a 0, b 0), |
|||
a |
2 |
b |
2 |
|||
|
|
|||||
|
|
|
|
описывает эллиптический цилиндр , в горизонтальных сечениях которого
один и тот же эллипс (рис. 33), а уравнение
z = ax |
2 |
, (a 0), |
|
описывает
параболический цилиндр , в вертикальных (перпендикулярно оси y) сечениях которого парабола (рис. 34).
Рис. 33 |
Рис. 34 |
Уравнение касательной плоскости к |
поверхности , заданной |
уравнением (42) в точке |
M |
0 |
(x |
, y , z |
0 |
) |
, как известно (см. [1]), имеет вид |
|
|||||
|
|
0 |
0 |
|
|
||||||||
|
A(x − x |
) + B( y − y ) + C(z − z |
0 |
) = 0, |
(45) |
||||||||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
||
где |
A = Fx '(x0 , y0 , z0 ), B = Fy '(x0 , y0 , z0 ), C = Fz '(x0 , |
y0 |
, z0 ). |
|
|||||||||
Нормалью (перпендикуляром) к поверхности в точке |
|
M |
0 |
(x |
, y |
, |
z |
0 |
) |
|||||||||||
|
|
0 |
0 |
|
|
|
||||||||||||||
называется нормаль к касательной плоскости в этой точке. Следовательно, |
|
|
|
|||||||||||||||||
N = ( A; B; C) = (F '(x |
, y |
, z |
0 |
); F |
'(x , y |
0 |
, z |
0 |
); F '(x , y |
0 |
, z |
0 |
)). |
|
|
|
|
|
||
x |
0 |
0 |
|
y |
0 |
|
z |
0 |
|
|
|
|
|
|
|
|||||
Пример 39. Написать уравнение касательной плоскости к параболоиду вращения z = x2 + y2 в точке с координатами (1, −1, 2).
Решение. F (x, y, z) = x2 + y2 − z. |
|
|
|
|||
Тогда |
F |
' = 2x, F '(1, −1, 2) = 2, F |
' = 2 y, F '(1, −1, 2) = −2, F |
' = −1. |
||
x |
x |
y |
y |
z |
|
|
Следовательно, уравнение касательной плоскости: |
|
|
||||
|
|
|
2(x −1) − 2( y +1) − (z − 2) = 0. |
|
◄ |
|
|
|
|
|
|
|
|
Пример 40. Найти линию пересечения параболоида z = x2 + y2 |
и плоскости |
|||||
z = 2x + 2 y. |
|
|
|
|
|
|
Решение. Линию пересечения образуют точки, удовлетворяющие системе уравнений:
