ИСиТ / 09.03.02 Интеллектуальные информационные системы и технологии / 2 курс 2 семестр / Алексеев Александр Борисович / Высшая математика / Методички от Алексеева (в порядке посылаемости) / 2сем / 7.1. Преобразование Лапласа (продолжение)

7.6. Сверткой двух функций , заданных на всей оси, называется функция , определяемая формулой

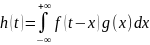, (7.18)

если интеграл сходится при любом значении . Свертка обозначается символом

.

Доказаны следующие свойства свертки.

1. , то есть свертка симметрична.

2. Свертка двух оригиналов является оригиналом, причем формула (7.18) принимает вид:

. (7.19)

Доказательство свойства 1. получается, если в интеграле (7.18) сделать замену переменной: .

Пределы интегрирования в (7.19) следуют из того, что

. ■

Теорема 7.11 (о свертке). Пусть , . Тогда свертка (7.19) имеет изображение

. (7.20)

Доказательство см. в [1]. ■

Пример 7.12. Найти оригинал для изображения

.

Решение. Разложим на произведение двух сомножителей и применим теорему о свертке. Тогда

. ►

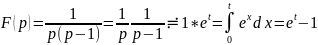Заметим, что аналогичное решение получается из теоремы об интегрировании оригинала. Еще один способ решения получится, если разложить дробь на простейшие:

.

Изображение (7.17) решения задачи Коши (7.14) при нулевых начальных условиях можно рассматривать как произведение двух изображений: и . Тогда решение задачи (7.14) получаем с помощью свертки (7.19) или (в силу симметрии) в виде

. (7.21)

Решим пример 6.14 (уравнение с нулевыми начальными условиями) с помощью преобразования Лапласа.

Решение. Для этого уравнения

, .

Формула (7.21) дает

,

что совпадает с решением примера 6.14. ►

7.7. Перечислим методы восстановления оригиналов.

1. Обратиться к таблице.

В книгах таблицы бывают разного размера, поэтому есть возможность найти нужный оригинал.

2. Разложение дроби на простейшие.

Если изображение – правильная дробь, следует ее разложить на простейшие и заглянуть в таблицу, где всегда есть оригиналы, соответствующие таким изображениям (см. пример 7.12).

3. Использование свертки.

Если изображение можно представить в виде произведения табличных изображений, то оригинал находится в виде свертки соответствующих оригиналов (см. пример 7.12). Причем такая операция может быть повторена неоднократно.

4. Вычисление интеграла на комплексной плоскости.

В теории функций комплексной переменной (см. [1]) доказано, что оригинал восстанавливается с помощью интеграла

,

где контуром интегрирования на плоскости комплексной переменной является вертикальная прямая, проходящая через значение , то есть в области регулярности функции .

7.8. Интегральным уравнением называется уравнение, содержащее неизвестную функцию под знаком интеграла.

Интегральное уравнение называется уравнением Вольтерра второго рода, если оно имеет вид:

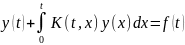, (7.22)

и уравнением Вольтерра первого рода в таком случае:

. (7.23)

Здесь – неизвестная функция, - заданные, при этом функция называется ядром интегрального уравнения (интегрального оператора).

Интегральное уравнение Вольтерра называется уравнением типа свертки, если ядро зависит только от разности аргументов, т.е. 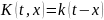. В этом случае уравнения (7.22) и (7.23) принимают вид:

, (7.24)

. (7.25)

Уравнения типа свертки (7.24) и (7.25), если функци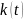и и являются оригиналами, решаются с помощью преобразования Лапласа. А именно, применив к уравнениям (7.24) и (7.25) преобразование Лапласа, по теореме о свертке получим:

(7.26)

. (7.27)

Здесь , , , уравнение (7.26) является преобразованием уравнения (7.24), а уравнение (7.27) – уравнения (7.25). Их решение:

, (7.28)

. (7.29)

Восстановив оригиналы для изображений (7.28) и (7.29), получим решение уравнений (7.24) и (7.25). ■

Пример 7.13. Решить уравнение

.

Решение. Применим преобразование Лапласа и воспользуемся таблицей оригиналов и изображений. Тогда

.

Решив это уравнение относительно 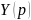, получим

.

Оригинал найдем с помощью теоремы о свертке:

. ►

Замечание. Уравнения Вольтерра второго рода всегда разрешимы. А уравнения типа свертки (7.24) всегда разрешимы на множестве оригиналов. Это видно из формулы (7.28). Если и – правильные дроби, то выражение тоже будет правильной дробью из-за единицы в знаменателе.

Уравнения Вольтерра первого рода не всегда разрешимы на множестве обычных оригиналов. Иногда их решениями являются так называемые обобщенные функции (см., например, [2]).

Пример 7.14. Решить уравнения

.

Решение. После преобразования Лапласа получим

.

Отсюда: . Решением уравнения является функция , решением уравнения : – производная дельта-функции (см. [2]). ►

7.9. Дельта-функция Дирака может быть определена как предел импульсных функций, а именно,

, (7.30)

где импульсная функция определяется условием:

.

Функция описывает прямоугольный импульс высотой с площадью, равной 1, и может быть выражена через функции Хевисайда:

), (7.31)

где .

Найдем изображение функции (выражения (7.31)) с помощью теоремы запаздывания. Получим

. (7.32)

Тогда, используя (7.30) и (7.32), изображение дельта-функции находим с помощью предельного перехода:

.

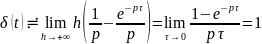Итак

,

а из теоремы о дифференцировании оригинала –

.

Литература.

1. Краснов М.Л., Киселев А.И., и др. «Вся высшая математика», т. 4, М., 2001.

2. Шилов Г.Е. «Математический анализ. Второй специальный курс» М., «Наука», 1965.

ф(t) = j т sin(t - т) d