
- •6. Обыкновенные дифференциальные уравнения
- •6.1. Обыкновенным дифференциальным уравнением
- •6.2. С разделенными переменными
- •Пример 6.1.
- •6.3. Однородным дифференциальным уравнением 1-го порядка
- •Пример 6.2.
- •6.4. Линейным дифференциальным уравнением 1-го порядка
- •Пример 6.3.
- •6.4. Уравнение Бернулли
- •Пример 6.4.
- •6.5. Уравнением в полных дифференциалах и интегрирующим множителем
- •Пример 6.4.
- •Пример 6.4.
]
Оглавление
6. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1
6.1. Обыкновенным дифференциальным уравнением 1
6.2. с разделенными переменными 3
Пример 6.1. 3
6.3. Однородным дифференциальным уравнением 1-го порядка 3
Пример 6.2. 4
6.4. Линейным дифференциальным уравнением 1-го порядка 4
Пример 6.3. 5
6.4. уравнение Бернулли 5
Пример 6.4. 6
6.5. Уравнением в полных дифференциалах и интегрирующим множителем 6
Пример 6.4. 6
Пример 6.4. 7
6. Обыкновенные дифференциальные уравнения
6.1. Обыкновенным дифференциальным уравнением
Обыкновенным дифференциальным уравнением называется уравнение, в которое, кроме независимой переменной и неизвестной функции, входят производные этой функции или ее дифференциалы.
Общий вид обыкновенного дифференциального уравнения:
 ,
(6.1)
,
(6.1)
где
 – независимая переменная и
– независимая переменная и
 – искомая функция этой переменной.
Число
– искомая функция этой переменной.
Число
 -
наивысший
порядок производных
неизвестной функции, входящих в уравнение,
называется порядком
дифференциального уравнения.
-
наивысший
порядок производных
неизвестной функции, входящих в уравнение,
называется порядком
дифференциального уравнения.
В частности, обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
 .
(6.2)
.
(6.2)
Решением
(частным решением) дифференциального
уравнения
называется любая функция
 ,
которая при подстановке в уравнение
обращает его в тождество.
,
которая при подстановке в уравнение
обращает его в тождество.
Частные случаи уравнений (6.1) и (6.2):
 ,
(6.3)
,
(6.3)
 (6.4)
(6.4)
называются дифференциальными уравнениями, разрешенными относительно старшей производной.
В простейшем случае, уравнение (6.4) имеет вид
 .
(6.5)
.
(6.5)
Нахождение его решений есть основная задача интегрального исчисления, и все множество этих решений дается формулой
 ,
(6.6)
,
(6.6)
где
–
какая-то первообразная функции
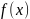 ,
,
 – произвольная постоянная. Таким
образом, уравнение (6.5) имеет семейство
решений, зависящее от произвольной
постоянной, при этом любое частное
решение получается из формулы (6.6) при
конкретных значениях постоянной
.
– произвольная постоянная. Таким
образом, уравнение (6.5) имеет семейство
решений, зависящее от произвольной
постоянной, при этом любое частное
решение получается из формулы (6.6) при
конкретных значениях постоянной
.
Аналогично,
уравнение (6.2) (или (6.4)) имеет семейство
решений
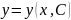 ,
зависящее
от произвольной постоянной, из которого
получаются частные решения при конкретных
значениях постоянной
.
Такое решение называется общим
решением
уравнения (6.2) (или (6.4)).
,
зависящее
от произвольной постоянной, из которого
получаются частные решения при конкретных
значениях постоянной
.
Такое решение называется общим
решением
уравнения (6.2) (или (6.4)).
Общим
решением
уравнения (6.1) (или (6.3)) является семейство
решений
 ,
зависящее
от произвольных постоянных
,
зависящее
от произвольных постоянных
 ,
из которого получаются частные решения
при конкретных значениях постоянных
.
,
из которого получаются частные решения
при конкретных значениях постоянных
.
Задача, в которой требуется найти решение дифференциального уравнения (6.4), удовлетворяющее начальному условию
 ,
(6.7)
,
(6.7)
где
 ,
,
 –
заданные числа, называется задачей
Коши.
–
заданные числа, называется задачей
Коши.
Доказана Теорема существования и единственности решения задачи Коши для уравнения 1-го порядка (6.4).
Пусть
функция
 непрерывна и имеет непрерывную частную
производную
непрерывна и имеет непрерывную частную
производную
 в окрестности точки с координатами (
,
).
Тогда задача Коши для уравнения (6.4)
с условием (6.7)
имеет
в этой окрестности единственное решение.
в окрестности точки с координатами (
,
).
Тогда задача Коши для уравнения (6.4)
с условием (6.7)
имеет
в этой окрестности единственное решение.
Если известно общее решение уравнения (6.4), то, используя условие (6.7), получим уравнение

для отыскания значения постоянной , соответствующего решению заданной задачи Коши.
Уравнение
(6.4)
может иметь решения, которые не получаются
из общего решения
ни при каком значении постоянной
.
Такие решения называются особыми
решениями.
Они
могут существовать только в окрестности
тех точек
 ,
где не выполнены условия теоремы
существования и единственности решения
задачи Коши. То же самое верно и для
уравнения
- го
порядка
(6.3).
(Подробнее (см.[.]).
Здесь мы особые решения рассматривать
не будем.)
,
где не выполнены условия теоремы
существования и единственности решения
задачи Коши. То же самое верно и для
уравнения
- го
порядка
(6.3).
(Подробнее (см.[.]).
Здесь мы особые решения рассматривать
не будем.)
Задача Коши для уравнения - го порядка (6.3) формулируется с помощью условий:
,
 ,
(6.8)
,
(6.8)
где
,
 –
заданные числа. Для этой задачи Коши
также доказана теорема
существования и единственности.
–
заданные числа. Для этой задачи Коши
также доказана теорема
существования и единственности.
Пусть
функция
 переменных
переменных
 непрерывна и имеет непрерывные частные
производные
непрерывна и имеет непрерывные частные
производные
 в окрестности точки с координатами (
,
).
Тогда задача Коши для уравнения (6.3)
с условиями (6.8)
имеет
в этой окрестности единственное решение.
в окрестности точки с координатами (
,
).
Тогда задача Коши для уравнения (6.3)
с условиями (6.8)
имеет
в этой окрестности единственное решение.
Если известно общее решение уравнения (6.3), зависящее от произвольных постоянных, то значения этих постоянных, соответствующие решению заданной задачи Коши, находятся из системы (6.8) уравнений с неизвестными.
