Добавил:

DANiilPESHov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Высшая математика

Файл:

3.1. 2-ой инт. (продолжение); Тройноый интеграл

.docx

Скачиваний:

Добавлен:

07.03.2023

Размер:

116.03 Кб

Скачать

☆

2. ДВОЙНОЙ ИНТЕГРАЛ (продолжение)

2.5. Если в области использовать полярные координаты точки (функция теперь рассматривается как функция двух переменных ) и область для построения интегральной суммы разбивать линиями постоянства (окружности) и (лучи, выходящие из полюса), то получившийся двойной интеграл называется двойным интегралом в полярных координатах и обозначается символом

Его вычисление для области в виде круга радиуса , центр которого совпадает с полюсом полярной системы координат, дается формулой

. (2.11)

Для области, представленной на рис 7, двойной интеграл в полярных координатах вычисляется по формуле

. (2.12)

Рис. 7.

Пример 2.2. Найти площадь поверхности сферы радиуса .

Решение. Эта сфера описывается уравнением: и состоит из двух одинаковых полусфер, верхней и нижней. Достаточно найти площадь верхней (см. рис.1 а)) и умножить на 2.

Функция, задающая верхнюю полусферу: . Найдем частные производные , и сосчитаем выражение . Получим

. (2.13)

Площадь верхней полусферы найдем при помощи двойного интеграла (2.10) с подынтегральной функцией (2.13), область интегрирования : круг радиуса R с центром в начале координат. Такой интеграл удобнее вычислять в полярных координатах (см. (2.11)):

Следовательно, вся площадь равна . ◄

Выбор системы координат при вычислении двойного интеграла зависит от вида области интегрирования и подынтегральной функции.

Пример 2.3. Найти объем тела, ограниченного цилиндрической поверхностью и плоскостями при условии (рис 8).

Рис. 8. Рис. 9.

Решение. Область интегрирования удобно (см. рис.9) разбить на две части: треугольник (заштрихован) и оставшаяся часть круга . При вычислении интеграла в первой части ( ) надо использовать декартовы координаты, а во второй ( ) – полярные. Тогда

. ◄

2.6. В двойном интеграле можно сделать общую замену переменных. Пусть переменные и являются функциями . Тогда справедлива формула

, (2.14)

где определитель вида:

. (2.15)

Он называется якобианом преобразования.

Приведем пример вычисления площади фигуры, ограниченной эллипсом, заданным каноническим уравнением , с помощью перехода к эллиптическим координатам . Эти координаты задаются формулами:

, (2.16)

причем для данной фигуры: , . Якобиан преобразования (2.16) равен

. (2.17)

Тогда

. (2.18)

3. ТРОЙНОЙ ИНТЕГРАЛ

3.1. Определение тройного интеграла аналогично определению двойного интеграла. Пусть ограниченная область трехмерного пространства и функция точки, определенная в этой области, т. е. функция, принимающая в каждой точке области определенное значение. Разобьем на частей , , …, , объемы которых обозначим через , , …, . Выберем в каждой подобласти точки , , …, и составим сумму произведений (она, как обычно, называется интегральной суммой)

. (3.1)

Пусть – максимальное расстояние между двумя точками подобласти (диаметр этой подобласти) и , – ранг разбиения.

Предел суммы (3.1) при , не зависящий ни от способа разбиения, ни от выбора точек , , …, , называется тройным интегралом от функции по области :

. (3.2)

Функция в этом случае называется интегрируемой в области .

Свойства тройного интеграла аналогичны свойствам двойного интеграла, так как аналогичны определения этих интегралов. А именно, имеют место свойства линейности, аддитивности и т.п. Можно также доказать, что, если функция непрерывна в области , то она в ней интегрируема. Имеют место теорема о «среднем», теорема об интегрировании неравенств и т.д.

3.2. Если в области , то из (3.2) следует, что тройной интеграл равен объему этой области:

. (3.3)

В этом состоит геометрический смысл тройного интеграла.

3.3. Введем в трехмерном пространстве декартову систему координат. Пусть в области задана интегрируемая функция , которую теперь можно рассматривать как функцию трех переменных , где – декартовы координаты точки . Так как интеграл – это предел интегральной суммы, независящий от способа разбиения области , разобьем область на подобласти (здесь удобнее подобласти нумеровать тремя индексами, а не одним) плоскостями, параллельными координатным плоскостям. В этом случае большинство подобластей являются параллелепипедами со сторонами , и , объем которых равен произведению . Тройной интеграл, полученный в результате такого разбиения, называется тройным интегралом в декартовых координатах и обозначается символом

. (3.4)

Пусть область – параллелепипед, ограниченный плоскостями, параллельными координатным плоскостям: , , . В этом случае все подобласти такого разбиения - параллелепипеды объема , где – длина участка разбиения интервала на оси , – длина участка разбиения интервала на оси , а – длина участка разбиения интервала на оси . Можно доказать, что вычисление тройного интеграла в декартовых координатах сводится к вычислению трех определенных интегралов. Верна следующая формула:

, (3.5)

причем интегралы в правой части (3.5) можно менять местами.

Если область – выпукла (см. рис. 10), то поверхность , ограничивающая область , пересекается не более чем в двух точках любой прямой. Тогда поверхность разбивается на две части: верхнюю и нижнюю, которые являются графиками двух однозначных функций. Пусть функция, соответствующая нижней части, – , верхней - . Трехмерная область проектируется на плоскость в виде двумерной области , а линия касания верхней и нижней частей поверхности – на границу области . Прямая, параллельная оси и проходящая через любую точку области , войдет внутрь области через поверхность и выйдет из нее через поверхность .

Рис. 10.

Доказано, что в этом случае вычисление тройного интеграла в декартовых координатах сводится к определенному и двойному интегралам по формуле:

. (3.6)

Двойной интеграл можно, в свою очередь, привести к повторному, как это показано в формулах (2.8) и (2.9).

В формуле (3.6) можно получить другой порядок интегрирования путем проектирования области на плоскость или на плоскость .

Если область не является выпуклой, ее следует разбить на удобные подобласти и применить для вычисления тройного интеграла свойство аддитивности.

Пример 3.1. Найти объем тела , ограниченного поверхностями и плоскостями .

Решение. Поверхности, ограничивающие тело сверху и снизу, пересекаются по линиям, которые получаются из решения системы уравнений

Кроме этого, тело по бокам ограничено плоскостями . Тогда в формуле (3.6) , , а область интегрирования – квадрат, ограниченный прямыми , . Следовательно, используя свойства четности (нечетности) подынтегральных функций, получим

. ◄

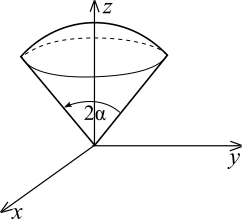
3.4. Цилиндрические координаты точки в трехмерном пространстве фактически представляют собой объединение координаты с полярными координатами на плоскости . А именно, положение точки определяется (см. рис. 11) тремя числами: , где

координата есть расстояние от точки до оси и – угол, образованный полуплоскостью, проходящей через ось и точку , с плоскостью . Угол отсчитывается от положительного направления оси против часовой стрелки. Точкам оси соответствует , координата для них неопределенна.

Связь между декартовыми и цилиндрическими координатами выражается формулами:

. (3.7)

Следовательно, для вычисления тройного интеграла в цилиндрических координатах, который имеет вид

, (3.8)

достаточно в формуле (3.6) двойной интеграл по области вычислять в полярных координатах ).

Рис. 11. Рис. 12.

Пример 3.2. Вычислить объем шара радиуса .

Решение. Из уравнения сферы, ограничивающей шар, получаем уравнения нижней и верхней полусфер:

Формулы (3.3) и (3.6) приведут к двойному интегралу:

где область – круг радиуса : . Этот двойной интеграл удобнее вычислять в полярных координатах. Тогда получим

. (3.9)

3.5. Сферические координаты точки в трехмерном пространстве (см. рис. 12) – это три числа: , где – длина отрезка , – угол, который полуплоскость, проходящая через ось и точку , образует с плоскостью , – угол, который отрезок образует с положительным направлением оси . При этом может изменяться от 0 до +∞, угол отсчитывается против часовой стрелки от положительного направления оси и может изменяться от 0 до (это тот же угол, что и в цилиндрических координатах), наконец, угол отсчитывается от положительного направления оси и может изменяться от 0 до .

Связь между декартовыми и сферическими координатами выражается формулами:

. (3.10)

Заметим, что началу координат, точке , соответствует , а значение двух других координат и неопределенно. Для всех точек, лежащих на оси , будет неопределенной координата , а для точек положительной полуоси и – для точек отрицательной полуоси.

Доказано, что тройной интеграл в сферических координатах имеет вид

. (3.11)

Его вычисление сводится к трем определенным (повторным) интегралам по переменным , и . Пределы интегрирования зависят от вида области .

Пример 3.3. Вычислить объем шарового сектора радиуса , угол в сечении которого равен (см. рис. 13).

Рис. 13. Рис. 14. Рис.15

Решение. Систему координат расположим так, что начало координат совпадает с вершиной конуса, а положительная полуось проходит через его ось симметрии. Тогда при вычислении тройного интеграла в сферических координатах (3.11) пределы интегрирования будут постоянными:

. (3.12)

З а м е ч а н и е. При шаровой сектор превращается в целый шар, и из (3.12) получается формула (3.9) объема шара. ◄

Удобство применения тех или иных координат для вычисления тройного интеграла зависит от вида области . Для сравнения рекомендуем решить этот пример в декартовой и цилиндрической системах координат.

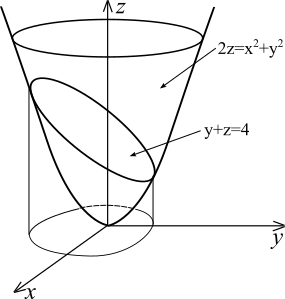
Приведем пример, в котором вместо обычных цилиндрических координат удобно применять координаты со сдвинутым полюсом.

Пример 3.4. Вычислить объем тела, ограниченного параболоидом и плоскостью .

Решение. Поверхности (см. рис. 14), ограничивающие тело сверху (плоскость) и снизу (параболоид), пересекаются по линии, которая получается из решения системы уравнений

Исключив переменную , получим (см. рис. 15) проекцию этой линии (границу области ) на плоскость : . Тогда, вводя на плоскости полярные координаты с помощью связи (с полюсом в точке (0,-1)), из формулы (3.6) получаем