
8.2. Интегрирование неравенств.
Теорема
1. Пусть
функции
и
– интегрируемы на
,
причем
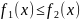 при
при
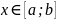 .
Тогда
.
Тогда
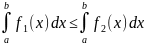 .
(8.10)
.
(8.10)
Доказательство следует из определения определенного интеграла и теоремы о предельном переходе в неравенстве. ■
Следствие.
Пусть
функция
– интегрируема на
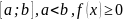 при
.
Тогда
при
.
Тогда
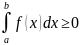 .
(8.11)
.
(8.11)
Замечание.
Если
интегрируемая функция
удовлетворяет строгому неравенству
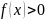 при
,
нельзя утверждать, что вместо (8.11) будет
выполняться строгое неравенство для
интеграла. Но для непрерывных функций
такое утверждение верно.
при
,
нельзя утверждать, что вместо (8.11) будет
выполняться строгое неравенство для
интеграла. Но для непрерывных функций
такое утверждение верно.
Теорема
2. Пусть
функция
– непрерывна на
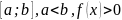 при
.
Тогда
при
.
Тогда
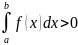 .
(8.12)
.
(8.12)
Доказательство.
По теореме Вейерштрасса существуют
наименьшее (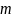 )
и наибольшее (
)
и наибольшее (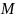 )
значения функции
,
которые достигаются на
,
причем в силу условия теоремы
)
значения функции
,
которые достигаются на
,
причем в силу условия теоремы
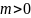 ,
,
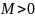 .
Тогда из теоремы 1 и (8.8) получается, что
.
Тогда из теоремы 1 и (8.8) получается, что
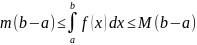 ,
(8.13)
,
(8.13)
откуда и следует утверждение теоремы. ■
Следствие.
Пусть
функции
и
– непрерывны на
,
причем
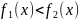 при
.
Тогда
при
.
Тогда
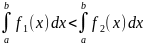 .
(8.14)
.
(8.14)
Замечание. Неравенство (8.13) верно для любой (принимающей значения любого знака) непрерывной функции.
Теорема 3. Пусть функция – интегрируема на промежутке . Тогда
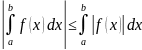 .
(8.15)
.
(8.15)
Доказательство следует из определения определенного интеграла, неравенства для модулей, называемого неравенством треугольника и теоремы о предельном переходе в неравенстве. ■
8.3. Теорема о среднем и ее обобщение
Теорема.
Пусть
функции
и
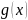 – непрерывны на
,
– непрерывны на
,
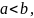 причем
функция
сохраняет
знак на
. Тогда
существует (хоть одно) число
причем
функция
сохраняет
знак на
. Тогда
существует (хоть одно) число
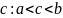 ,
такое что
,
такое что
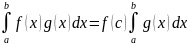 .
(8.16)
.
(8.16)
Доказательство.
Пусть сначала
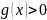 .
Аналогично
с (8.13)
имеет место неравенство
.
Аналогично
с (8.13)
имеет место неравенство
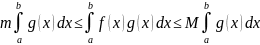 .
(8.17)
.
(8.17)
Разделим
неравенство (8.17)
на интеграл
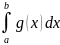 ,
который в силу (8.12) является положительным
числом.
Получим неравенство
,
который в силу (8.12) является положительным
числом.
Получим неравенство
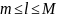 ,
где
,
где
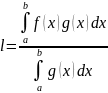 .
.
По
теореме Больцано-Коши существует
хотя бы одно число
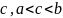 ,
такое что
,
такое что
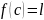 .
.
Если
функция
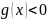 ,
то введем функцию
,
то введем функцию
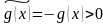 ,
для которой, как доказано, верно равенство
(8.16).
То есть
,
для которой, как доказано, верно равенство
(8.16).
То есть
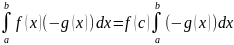 .
.
Остается сократить на (-1). ■
Следствие
(теорема
о среднем).
В
частности,
если
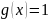 ,
а
-
непрерывна
на
,
а
-
непрерывна
на
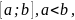 то
существует число
такое, что
то
существует число
такое, что
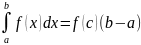 (8.18)
(8.18)
или
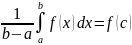 .
(8.19)
.
(8.19)
(Выражение в левой части равенства (8.19) называется средним значением функции по промежутку ).
Геометрически
равенство (8.18)
означает, что существует такое число
,
что площадь криволинейной трапеции
(8.5)
равна площади прямоугольника с основанием
и высотой, равной
 (см. рис.22).
(см. рис.22).
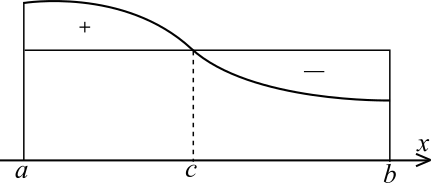
Рис. 22. Геометрическая интерпретация теоремы о среднем
8.4. Формула ньютона-лейбница
Теорема
Барроу. Пусть
функция
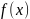 непрерывна на интервале
непрерывна на интервале
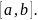 Введем функцию
Введем функцию
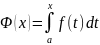 ,
,
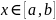 .
(8.20)
.
(8.20)
Тогда
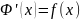 .
.
То есть интеграл с переменным верхним пределом (8.20) от непрерывной функции является первообразной подынтегральной функции.
Доказательство. Пусть Δx > 0 . Рассмотрим
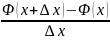 =
=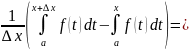
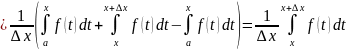 .
.
По
теореме
о среднем
существует такая точка
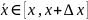 ,
что
,
что
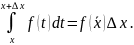
Тогда
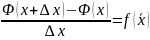 .
.
Из
условия
следует, что если
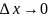 ,
то
,
то
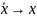 .
Поскольку функция
непрерывна, то из того, что
,
следует, что
.
Поскольку функция
непрерывна, то из того, что
,
следует, что
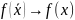 .
Тем самым доказано существование предела
справа. Аналогично доказывается, что
предел слева существует и совпадает с
пределом справа. Тогда
.
Тем самым доказано существование предела
справа. Аналогично доказывается, что
предел слева существует и совпадает с
пределом справа. Тогда
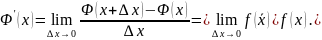
Теорема доказана. ■
Из теоремы Барроу вытекает формула Ньютона – Лейбница - способ вычисления определённого интеграла в случае непрерывной подынтегральной функции.
Теорема.
Пусть функция
непрерывна на интервале
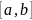 и
и
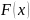 – ее первообразная (
– ее первообразная (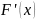 =
).
Тогда
=
).
Тогда
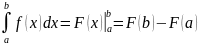 .
(8.21)
.
(8.21)
Доказательство.
Для функции
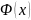 ,
определенной формулой (8.20) верны свойства:
,
определенной формулой (8.20) верны свойства:
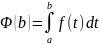 ,
,
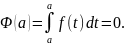
Следовательно,
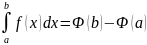 .
(8.22)
.
(8.22)
Поскольку
две первообразные функции
отличаются на постоянную
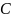 ,
и верно очевидное равенство
,
и верно очевидное равенство
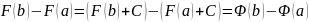 ,
,
то
в последнем равенстве (8.22) функцию
можно заменить на
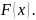 Тогда, введя обозначение (называемое
подстановкой):
Тогда, введя обозначение (называемое
подстановкой):
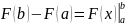 ,
,
получим формулу (8.21). ■
Пример.
Вычислить
интеграл
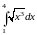 .
.
Решение. По формуле 1 таблицы 2 находим первообразную и подставляем пределы
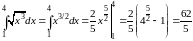 ◄
◄
