8. Решение систем линейных уравнений в excel
Сначала рассмотрим решение системы линейных уравнений методом Крамера. Для этого используем уже решенный пример 9.
В EXCEL реализована функция вычисления определителей (см. п.7). Запишем матрицу коэффициентов и матрицы, полученные из нее заменой по очереди всех столбцов на столбец свободных членов. Листинг вычислений представлен на рис. 8:
Рис. 8
Матрицы
записаны в диапазонах
,
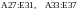а значения определителей – в ячейках
.
Столбец свободных членов – в G2:G6.
Решение системы – в I2:I6.
Тот
же пример
решим с помощью обратной
матрицы. В
EXCEL
реализованы функции для нахождения
обратных матриц и перемножения матриц
(см. п.7). Листинг решения представлен на
рис. 9. В диапазоне
записана матрица коэффициентов, в
ячейках
– вектор свободных членов, в диапазоне
обратная матрица, в ячейках
– решение системы, полеченное как
результат умножения матрицы
на матрицу
.
Рис. 9
Предложим еще один способ решения линейных систем в EXCELL. Возможно, для систем он не покажется эффективным, однако знакомство с ним полезно для решения задач оптимизации, в частности задач линейного программирования. Инструментом для этого метода служит процедура Поиск решения, которая находится в Надстройках. После вызова процедуры появляется окно, представленное на рис. 11.
Покажем решение системы на примере.
►Пример
16. Решить
систему
Рис. 10
В
ячейки
введена матрица коэффициентов
уравнений системы, в
– коэффициенты последнего уравнения,
в ячейки G3:G6
- столбец свободных членов. Ячейки B1:E1
отведем для значений неизвестных. В
ячейках F3:F6
сосчитаем сумму произведений коэффициентов
каждого уравнения на неизвестные (для
этого воспользуемся встроенной функцией
СУММПРОИЗВ). Выберем ячейку F6
в качестве целевой и вызовем процедуру
Поиск
решения.
В окошке установим, что целевая ячейка
должна быть равной
свободному члену последнего уравнения,
и заполним поля. В поле «изменяя
ячейки»
введем B1:E1.
В поле «ограничения»
будем вводить первые
уравнения. А именно, значение в ячейке
F3
должно равняться заданному значению в
ячейке G3
(1-е уравнение). Аналогично добавляем
два других уравнения. После заполнения
всех полей нажимаем
.
Решение системы находится в ячейках B1:E1.
Рис. 11
Литература
1. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1977.
2. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Издательство «Лань», 1998.
3. Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая математика: Учебник. Т. 1. – М.: Эдиториал УРСС, 2000.
4. Данко П.Е, Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1999. Ч.1.- 304 с. - Ч.2. - 416 с.
5. Фридман Г. Н., Леора С.Н. Математика & Mathematica. Избранные задачи для избранных студентов. – Невский Диалект, БХВ-Петербург , 2010, 299 с.
6. Пащенко И.Г. Excel 2007. -М.: Эксмо, 2009. -496 с.
Введение 3
1. Матрицы и действия с матрицами 4
1.1. Основные понятия. 4
1.2. Действия с матрицами. 5
2. Определители и их свойства 9
3. Обратная матрица. Решение матричных уравнений 14
4. Ранг матрицы 17
5. Системы линейных уравнений 18
5.1 Основные понятия. 18
5.2. Решение систем по формулам Крамера. 20
5.3. Решение системы с помощью обратной матрицы. 22
5.4. Исследование систем линейных уравнений. Метод Гаусса 23
5.5. Однородные системы. 28
6. Собственные значения и собственные векторы матрицы 30
7. Действия с матрицами на компьютере в EXCEL 33
Литература 40