5. Системы линейных уравнений

5.1 Основные понятия.

Системой линейных уравнений с неизвестными (линейной системой) называется система вида

(7)

где − заданные числа. Числа называются коэффициентами системы, а числа - свободными членами.

Линейная система называется однородной, если все свободные члены равны нулю, т.е.

(8)

В противном случае линейная система называется неоднородной.

Решением системы (7) называется упорядоченная совокупность чисел:

, (9)

при подстановке которых вместо каждое уравнение системы обращается в тождество.

Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Однородная система (8) всегда совместна, так как она имеет очевидное решение: . Нулевое решение однородной системы называется тривиальным.

Две системы называются равносильными или эквивалентными, если любое решение одной из них является также решением и другой, и обратно, т.е. они имеют одно и то же множество решений. В частности, любые две несовместные системы являются эквивалентными.

Линейную систему можно записать в матричной форме. Введем матрицы:

– матрица коэффициентов при неизвестных,

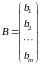– матрица-столбец свободных членов,

– матрица-столбец неизвестных.

Тогда систему (7) можно записать в виде матричного уравнения , а решение (9) в виде матрицы-столбца . Иногда для экономии места в ответах упражнений будем его записывать в виде матрицы-строки.

Матрица коэффициентов называется основной матрицей системы. Матрица, составленная из коэффициентов и свободных членов

называется расширенной матрицей системы.

Выражение «решить систему» означает, что надо выяснить, совместна ли система, а в случае совместности – найти все ее решения

5.2. Решение систем по формулам Крамера.

Теорема Крамера.

Пусть дана система, в которой число уравнений совпадает с числом неизвестных

(10)

Если определитель основной матрицы системы

, (11)

не равен нулю, то система имеет единственное решение , где

Определители , получены из определителя заменой соответствующего столбца на столбец свободных членов.

►Пример 6. По формулам Крамера найти решение системы уравнений

Решение. Вычислим определители и найдем решение:

Ответ: .◄

Упражнения.

Решить системы по формулам Крамера:

1) 2) 3)

Ответы: 1) , 2) , 3) .

5.3. Решение системы с помощью обратной матрицы.

Система из уравнений с неизвестными в матричной форме имеет вид ,

где , , .

Если матрица невырожденная, то система имеет единственное решение, которое вычисляется по формуле (5)

.

►Пример 7. С помощью обратной матрицы найти решение системы

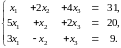
Решение. Проведем необходимые вычисления:

.

Ответ: . ◄

Упражнения.

Найти решение систем с помощью обратной матрицы:

а) б) в)

г)

Ответы: а) ; б) ; в) г) .