
Добавил:
DANiilPESHov
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:ИСиТ / 09.03.02 Интеллектуальные информационные системы и технологии / 2 курс 2 семестр / Алексеев Александр Борисович / Высшая математика / Высшая математика / Пробник целой методички / Методичка_ОЛЛ(2).docx

 .
.

 ,
функция:
,
функция:
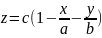 .
Тогда формула (2.7) принимает вид:
.
Тогда формула (2.7) принимает вид: .
◄
.
◄ ,
,

 вычисляется с помощью интеграла вида
(2.5), где роль подынтегральной функции
играет
вычисляется с помощью интеграла вида
(2.5), где роль подынтегральной функции
играет
 .
То есть площадь такой поверхности
.
То есть площадь такой поверхности .
(2.10)
.
(2.10)