
- •2022 Г. СПбГут им. Проф. М. А. Бонч-Бруевича Санкт-Петербург, пр. Большевиков, д. 22
- •9. Несобственные интегралы.
- •9.1. Несобственный интеграл 1-го рода.
- •Пример 1. Интеграл сходится при и расходится при .
- •Пример 2. Интеграл .
- •Пример 3. Интеграл
- •Теорема 1.
- •Теорема 2.
- •Теорема 3.
- •Теорема 4.
- •Пример 4. Выяснить сходится или расходится интеграл
- •Теорема 5.
- •Пример 5. Исследовать на сходимость интеграл .
- •9.2. Несобственный интеграл 2-го рода.
- •Пример 1. Интеграл сходится при и расходится при .
- •Пример 2. Исследовать на сходимость интеграл .
- •Теорема 1.
- •Пример 3. При исследовать на сходимость интеграл (гамма-функцию)
- •Пример 4. Исследовать на сходимость и вычислить интеграл .
- •Литература
- •1. Функции нескольких вещественных переменных. Основные понятия
- •Пример 1.1. Найти частные производные функции
- •Пример 1.2. Найти частные производные второго порядка функции
- •Пример 1.3. В точке найти градиент функции
- •Пример 1.4. В точке найти производную по направлению градиента функции
- •Пример 1.5. Исследовать на экстремум функцию
- •Пример 1.6. В кольце найти наибольшее и наименьшее значения функции
- •2. Двойной интеграл
- •Пример 2.1. Найти объем пирамиды, ограниченной плоскостями
2. Двойной интеграл
2.1. Пусть в
ограниченной плоской области
определена функция точки
 .
Разобьем область
на
подобластей
.
Разобьем область
на
подобластей
 (см. рис. 3). Обозначим через
(см. рис. 3). Обозначим через
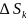 площадь подобласти
площадь подобласти
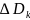 ,
через
,
через
 – ее диаметр (наибольшее расстояние
между двумя любыми точками
).
Введем ранг разбиения
– ее диаметр (наибольшее расстояние
между двумя любыми точками
).
Введем ранг разбиения
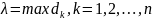 .
В каждой подобласти
выберем точку
.
В каждой подобласти
выберем точку
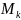 и составим интегральную сумму
и составим интегральную сумму
 .
(2.1)
.
(2.1)
Двойным
интегралом от функции
по области
называется предел интегральной суммы
при
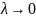
 ,
(2.2)
,
(2.2)
если этот предел существует и конечен независимо от разбиения области и выбора точек . Функция точки в этом случае называется интегрируемой в области .
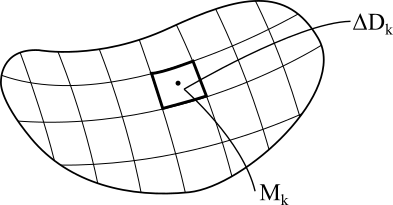
Рис. 3.
Так как алгоритм
определения двойного интеграла повторяет
соответствующий алгоритм для определенного
интеграла, то свойства двойного
интеграла аналогичны свойствам
определенного интеграла. А именно, имеют
место свойства линейности, аддитивности
и т.п. В частности, если
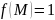 ,
то
,
то
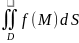 равен площади области
,
то есть
равен площади области
,
то есть
 .
(2.3)
.
(2.3)
Можно доказать, что, если функция непрерывна в области , то она в ней интегрируема. Верны также теорема о «среднем», теорема об интегрировании неравенств и т.д.
2.2. Пусть функция
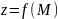 непрерывна в области
и принимает положительные значения.
Доказано, что
равен объёму тела, ограниченного
сверху графиком функции
,
с боков – цилиндрической поверхностью,
вырезающей на плоскости
непрерывна в области
и принимает положительные значения.
Доказано, что
равен объёму тела, ограниченного
сверху графиком функции
,
с боков – цилиндрической поверхностью,
вырезающей на плоскости
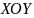 область
,
и снизу – плоскостью
(рис. 4), то есть
область
,
и снизу – плоскостью
(рис. 4), то есть
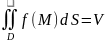 .
(2.4)
.
(2.4)
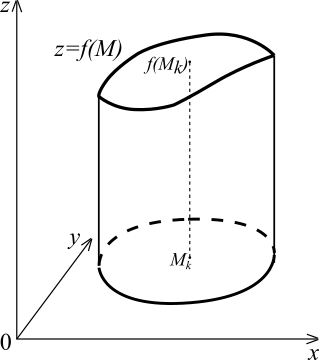
Рис. 4.
2.3. Введем на
плоскости декартову систему координат.
Пусть в области
задана интегрируемая функция
,
которую теперь можно рассматривать как
функцию двух переменных
,
где
– декартовы координаты точки
.
Так как интеграл – это предел интегральной
суммы, независящий от способа разбиения
области
,
разобьем область
на подобласти
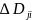 (здесь удобнее подобласти нумеровать
двумя индексами, а не одним) линиями,
параллельными осям координат. В этом
случае большинство подобластей разбиения
(кроме приграничных) будут прямоугольниками
площади, равной произведению
(здесь удобнее подобласти нумеровать
двумя индексами, а не одним) линиями,
параллельными осям координат. В этом
случае большинство подобластей разбиения
(кроме приграничных) будут прямоугольниками
площади, равной произведению
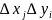 ,
где
,
где
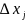 – длина стороны участка разбиения,
параллельной оси
– длина стороны участка разбиения,
параллельной оси
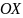 ,
а
,
а
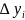 – длина стороны участка разбиения,
параллельной оси
– длина стороны участка разбиения,
параллельной оси
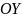 .
Двойной интеграл, полученный в результате
такого разбиения, называется двойным
интегралом в декартовых координатах
и обозначается символом
.
Двойной интеграл, полученный в результате
такого разбиения, называется двойным
интегралом в декартовых координатах
и обозначается символом
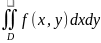 .
(2.5)
.
(2.5)
Пусть область
– прямоугольник со сторонами, параллельными
осям координат:
,
.
Тогда подобное разбиение будет содержать
только прямоугольники площади
,
где
– длина участка разбиения интервала
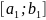 на оси
,
а
– длина участка разбиения интервала
на оси
,
а
– длина участка разбиения интервала
 на оси
,
и можно доказать, что вычисление
двойного интеграла в декартовых
координатах сводится к вычислению
двух определенных интегралов. Верны
следующие формулы:
на оси
,
и можно доказать, что вычисление
двойного интеграла в декартовых
координатах сводится к вычислению
двух определенных интегралов. Верны
следующие формулы:
 ,
(2.6)
,
(2.6)
 .
(2.7)
.
(2.7)
Если область – выпукла (см. рис. 5), то формулы (2.6) и (2.7) принимают вид:
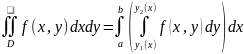 ,
(2.8)
,
(2.8)
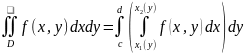 .
(2.9)
.
(2.9)
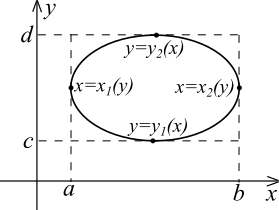
Рис. 5.
Здесь
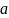 и
(
и
и
(
и
 )
– пределы, в которых зажата область
по оси
(по оси
),
)
– пределы, в которых зажата область
по оси
(по оси
),
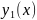 (
(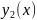 )
– функция, графиком которой является
нижняя (верхняя) часть границы, а
)
– функция, графиком которой является
нижняя (верхняя) часть границы, а
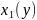 (
(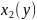 )
– функция, графиком которой является
левая (правая) часть границы.
)
– функция, графиком которой является
левая (правая) часть границы.
Интегралы в правой части формул (2.6) - (2.9) дают способ вычисления двойного интеграла в декартовых координатах и называются повторными. Доказательства формул (2.8) и (2.9) получаются из (2.6) и (2.7), соответственно, если поместить область в прямоугольник (см. рис. 5), продолжить на него функцию нулем и применить свойство аддитивности.
Для вычисления двойного интеграла по любой области следует разбить ее на удобные для формулы (2.7) (или (2.8)) подобласти и применить свойство аддитивности.
