Пример 1.3. В точке найти градиент функции
.
Решение. Находим частные производные:
,
.
В точке
,
.
Тогда
.
◄
Пример 1.4. В точке найти производную по направлению градиента функции
.
Решение. По формуле (1.27)
.
(Рекомендуем доказать, что, если применить формулу (1.23), получится тот же результат). ◄
1.11. Точка называется точкой локального максимума (точкой локального минимума) функции , если у точки существует окрестность такая, что для любой точки из этой окрестности выполняется неравенство
.
Точки локальных максимумов и минимумов функции называются точками экстремума функции.
Верно следующее утверждение (необходимое условие экстремума). Пусть точка – точка экстремума функции и в этой точке существуют частные производные и . Тогда в этой точке
и
.
(1.29)
Условие (1.29) равносильно тому, что в точке
,
(1.30)
где
- нулевой вектор.
Заметим, что условие (1.29) необходимо для экстремума, но не достаточно. Есть примеры функций, у которых нет экстремумов, но существуют точки, в которых первые частные производные равны нулю. Поэтому любые точки, в которых выполнено условие (1.29) называются стационарными точками.
Пусть – стационарная точка функции . Пусть в этой точке существуют вторые частные производные
.
Введем
.
Достаточным условием экстремума
функции
в точке
является следующее утверждение:
если
,
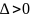то функция
имеет в точке
экстремум, причем максимум, если
(или
),
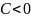и минимум, если
(или
);
если
,
то точка
точкой экстремума не является;
если
,
то необходимо дополнительное исследование.
Пример 1.5. Исследовать на экстремум функцию
.
Решение. Частные производные первого порядка найдены в примере 1.3. Система (1.29) в этом случае имеет вид:
Следовательно, решая систему, получим координаты стационарной точки:
Частные производные второго порядка:
,
,
.
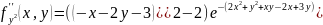Следовательно,
,
.
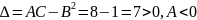Тогда в точке (1, -2) у функции максимум, причем максимальное значение функции
.
◄
1.12. Задача об отыскании наибольшего и наименьшего значений непрерывной функции в замкнутой области решается по следующей схеме: сначала находят стационарные точки внутри области и на границе области, а также точки, в которых производные не существуют, затем вычисляют значения функции во всех этих точках и среди них выбирают наибольшее и наименьшее.
Пример 1.6. В кольце найти наибольшее и наименьшее значения функции
В кольце
найти наибольшее и наименьшее значения
функции
.
Решение. Найдем стационарные точки, приравняв нулю частные производные первого порядка:
Точка
принадлежит области
,
значение функции в ней равно
.
Граница области
состоит из двух окружностей:
и
.
Первая из них описывается параметрически:
.
На ней функция зависит от одной переменной
.
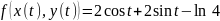Ее производная
равна нулю при
.
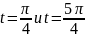Вычислим значения функции в этих точках
и добавим значение функции в точке
,
соответствующей (в силу периодичности
функции) концам промежутка
.
Получим
.
Аналогично на
второй окружности (
)
получаем три значения функции
.
Из полученных семи значений и выбираем
наибольшее:
и наименьшее:
.
(Рекомендуем проверить с помощью вторых производных, что в точке нет экстремума). ◄