Пример 3. При исследовать на сходимость интеграл (гамма-функцию)

.

Решение. Разобьем интеграл на сумму двух слагаемых, каждое из которых содержит только одну особенность:

.

Первое слагаемое при является несобственным интегралом 2-го рода, который сходится по признаку сравнения со степенной функцией, и является обычным определенным интегралом при .

Второе слагаемое – несобственный интеграл 1-го рода, который также сходится. Сравним при подынтегральную функцию с функцией . Из примера 2 п. 4.4 следует, что , т.е. для заданного числа существует число такое, что из неравенства следует неравенство . Остается сослаться на пример 1 и теоремы 1 и 3 п. 9.1. ◄

Пример 4. Исследовать на сходимость и вычислить интеграл .

Решение. Разобьем аналогичным образом интеграл на сумму двух слагаемых:

.

Первое слагаемое является несобственным интегралом 2-го рода, подынтегральная функция в нуле стремится к бесконечности. Второе слагаемое – несобственный интеграл 1-го рода.

Для этого второго интеграла, так как , верна оценка

. (9.10)

Так как показатель степени 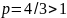, из теоремы 3 и примера 1 п. 9.1 следует, что второй интеграл сходится.

Для первого интеграла, так как , верна другая оценка (с показателем степени )

, (9.11)

которая, благодаря признаку сравнения со степенной функцией и примеру 1, доказывает, что и первый интеграл сходится.

Оценки (9.10) и (9.11) вместе доказывают, что наш интеграл сходится. Для его вычисления надо найти предел

. (9.12)

Неопределенный интеграл берется с помощью замены переменной: . Тогда

. (9.13)

Последний интеграл в (9.13) найден в примере 2 п.7.6.2. Подставляя в (9.12), получим

. ◄

Литература

1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. (В 3-х томах). — М. 2003. т.1— 680с.

2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. (В 3-х томах). — М. 2003. т.2— 864с.

3. Краснов М.Л. Вся высшая математика. Т.1. /М, Л. Краснов, Л. И. Киселев, М. И. Макаренко. – М., 2003, – 328с.

4. Краснов М.Л. Вся высшая математика. Т.2. /М, Л. Краснов, Л. И. Киселев, М. И. Макаренко. – М., 2004, – 192с.

5. Берман Г.Н. Сборник задач по курсу математического анализа. – М., 1985.–384с.

6. Алексеев А.Б., Филиппова А.Ф. Элементы векторной алгебры и аналитической геометрии. Учебно-методическое пособие. СПб ГУТ, 2019,– 46с.

1. Функции нескольких вещественных переменных. Основные понятия

1.1. Говорят, что задана функция двух независимых переменных , если задан закон, т. е. правило соответствия между парами чисел 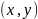и числами . При этом независимые переменные и называются аргументами, а зависимая переменная   – значением этой функции 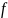. Каждой паре аргументов и соответствует определенная точка на координатной плоскости с координатами , и вместо того, чтобы говорить о значении функции при значениях аргументов и , можно говорить о значении функции в точке . Функция может быть определена на всей плоскости или только в какой-то ее части, в некоторой области , которая называется областью определения функции. Множество возможных значений чисел для функции называется областью ее значений.

Если функция задана аналитически, то есть переменные , и связаны некоторым уравнением, то область определения функции получается из возможности выполнить указанные действия. В частности, если функция есть многочлен от и , например, , то можно считать, что эта функция определена на всей плоскости. Формула задает функцию при условии: . Это условие означает, что область определения функции - круг с центром в начале координат и радиусом, равным .

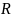Графически функция двух переменных может быть изображена в виде поверхности в трехмерном пространстве с декартовой системой координат . В частности, график функции – полусфера, расположенная над областью определения , а график функции – гиперболическая поверхность, имеющая седловую точку с координатами (0, 0).

Окрестностью точки (обозначение: ) называется множество точек , удовлетворяющих строгому неравенству: , т.е. внутренность круга с центром в точке любого радиуса . Если требуется указать радиус круга, например, , то такая окрестность называется -окрестностью и обозначается .

Точка называется внутренней точкой множества , если существует окрестность целиком принадлежащая этому множеству ( ). Точка называется граничной точкой множества , если любая окрестность содержит точки, как принадлежащие множеству , так и не принадлежащие множеству . Все множество граничных точек образует границу множества . Если множество содержит свою границу, то оно называется замкнутым, если множество не содержит границу, то оно называется открытым.

Примером замкнутого множества является область, описываемая неравенствами: 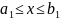, . Это - прямоугольник со сторонами, параллельными осям координат, причем граница этого прямоугольника, состоящая из отрезков, лежащих на прямых: , также включается в область. Неравенства , определяют только внутренние точки прямоугольника и, следовательно, - открытую область. Любая окрестность также является открытым множеством.

Аналогично определяются функция независимых переменных 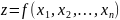, ее область определения и область значений. Все множество последовательностей вида 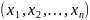называется –мерным пространством и обозначается , сами последовательности – точками пространства , а числа – координатами этой точки.

Аналогично окрестностью точки называется множество точек , удовлетворяющих неравенству: , вводятся понятия внутренней и граничной точки, замкнутого и открытого множества в пространстве .

В основном дальше рассматриваются функции двух переменных, сформулированные утверждения нетрудно перенести на функции переменных.

1.2. Введем понятие предела для функции двух переменных.

Пусть функция определена во всех точках , достаточно близких к точке , за исключением, может быть, ее самой. Число называется пределом функции при стремлении точки к точке , обозначение:

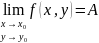или ,

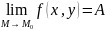если для любого заданного положительного числа существует такое положительное число , что выполняется неравенство

. (1.1)

Заметим, что неравенства в (1.1) могут быть заменены на условие: (точки принадлежат -окрестности точки ).

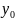Обращаем внимание, что и стремятся к своим предельным значениям и независимо друг от друга. При этом предполагается, что исключена пара значени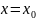й и (точка не совпадает с ). Если точка лежит на границе той области, в которой определена , то , стремящаяся к , должна принадлежать области, в которой определена функция .

Пусть имеется какая-либо пронумерованная последовательность точек , стремящаяся к , т. е. такая, что последовательность имеет предел , а последовательность имеет предел . Доказано, что если последовательность чисел для любой такой последовательности точек имеет один и тот же предел , то число есть предел функции при стремлении к в смысле сформулированного выше определения.

Так как определение (1.1) практически совпадает с определением предела функции одного вещественного переменного, теоремы о пределах сохраняются для функций двух переменных.

Кроме предельного перехода (1.1), можно рассматривать повторные пределы, соответствующие предельному переходу сначала по при постоянном , отличном от , а затем по , или наоборот:

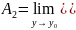или (1.2)

Из существования предела в смысле двух переменных (1.1) следует существование и совпадение повторных пределов: . Обратное – неверно.

1.3. Пусть функция определена в точке и во всех точках , достаточно близких к . Функция называется непрерывной в точке , если

, или . (1.3)

Определение (1.3) также совпадает с определением непрерывности функции одного вещественного переменного, поэтому теоремы о свойствах непрерывных функций сохраняются для функций двух переменных.

Приведем очевидное следствие, которое вытекает из определения непрерывности функции. Если функция двух переменных непрерывна в точке и, если мы положим , то функция одной переменной непрерывна в точке . Аналогично, непрерывна в точке .

Функция называется непрерывной в некоторой открытой области, если она непрерывна в каждой точке этой области (внутренней точке).

Функция называется непрерывной в замкнутой области, если она непрерывна в каждой внутренней точке этой области, а в граничных точках соотношение (1.3) выполняется при любом стремлении точек изнутри области.

Пусть - ограниченная замкнутая область на плоскости и непрерывная в функция. Такая функция обладает свойствами, аналогичными свойствам функции одной независимой переменной, непрерывной в конечном замкнутом промежутке. Доказательства этих свойств, по существу, те же, что и доказательства для функции одной независимой переменной. Сформулируем лишь результаты.

1. Функция ограничена в , т. е. существует такое положительное число , что 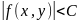для всех .

2. Функция достигает в наибольшего и наименьшего значений (теорема Вейерштрасса).

1.4. Допустим, что у функции переменная сохраняет постоянное значение и меняется только , то есть функция становится функцией одного переменного и можно вычислить ее приращение и производную в точке . Обозначим это приращение функции через (такое приращение называется частным приращением):

.

Частной производной первого порядка или функции по переменной в точке называется предел

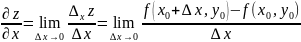, (1.4)

если он существует и конечен.

Если имеет частную производную по , то она, как известно, является непрерывной функцией аргумента при фиксированном .

Точно так же определяется частное приращение

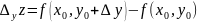
и частная производная первого порядка или функции по переменной в точке , вычисленная в предположении, что не меняется.

То есть

. (1.5)

Так как определения (1.4) и (1.5) совпадают с определением производной функции одной переменной, то при вычислении частных производных используются обычные правила и приемы дифференцирования.

Аналогично через частные приращения определяются частные производные функции независимых переменных .

1.5. Приведем формулы для производных сложных и неявных функций.

Пусть функция зависит через посредство и от одной независимой переменной , т. е. аргументы и сами являются функциями , имеющими производные и . Тем самым задана сложная функция . Пусть частные производные и непрерывны как функции двух переменных. Определим производную функции по . Если независимой переменной задать приращение , то функции и получат соответственно приращения и , а получит приращение :

. (1.6)

Из формулы конечных приращений (см. [.]) приращение (1.6) (такое приращение называется полным приращением) можно написать в виде:

,

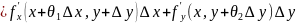где 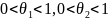. Разделим обе части этого равенства на . Тогда

. (1.7)

Устремим к нулю, тогда и также будут стремиться к нулю. В силу непрерывности всех участвующих в (1.7) функций в пределе получим

. (1.8)

Предположим, в частности, что роль независимой переменной играет переменная т. е. что функция зависит от переменной как непосредственно, так и через переменную . Принимая во внимание, что в этом случае , из равенства (1.8) следует

. (1.9)

Производная (1.9) называется полной производной от по в отличие от частной производной .

Доказанное правило дифференцирования сложных функций применяется для нахождения производной неявной функции. Положим, что уравнение

(1.10)

определяет неявную функцию , имеющую производную .

Продифференцируем уравнение (1.10), используя формулу (1.9). Тогда

,

откуда

. (1.11)

Пусть функция зависит через посредство и от двух независимых переменных и , т. е. аргументы и сами являются функциями , имеющими частные производные. Тем самым задана сложная функция . Аналогично формуле (1.9) доказываются правила дифференцирования:

, (1.12)

. (1.13)