9.2. Несобственный интеграл 2-го рода.

Здесь мы рассмотрим вопрос определения интеграла для ограниченных интервалов в случае, когда подынтегральная функция обращается в бесконечность в какой-то точке интервала. Такие интегралы называются несобственными интегралами 2-го рода.

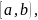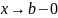Пусть функция непрерывна на интервале причем при . Тогда несобственный интеграл определяется равенством

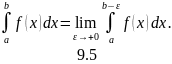
Если предел существует и конечен, то говорят, что интеграл сходится, и предел берется за значение интеграла, а если предел не существует или бесконечен, то говорят, что интеграл расходится.

Аналогично определяется несобственный интеграл, если особой точкой является другой край интервала. А именно, пусть функция непрерывна на интервале , причем при , тогда несобственный интеграл определяется равенством

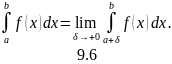
В обоих случаях смысл определения состоит в том, что нужно отойти от точки, в которой функция стремится к бесконечности, вовнутрь интервала, а затем расстояние, на которое отошли, устремить к нулю.

Как двойной предел определяется несобственный интеграл в том случае, когда функция стремится к бесконечности в обеих граничных точках интервала. А именно, пусть функция непрерывна на интервале , причем при и . Тогда несобственный интеграл определяется равенством

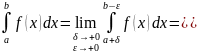
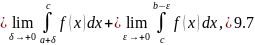
где – произвольное число.

Аналогично, через двойной предел, определяется несобственный интеграл в том случае, когда функция стремится к бесконечности во внутренней точке интервала.

Пусть функция непрерывна на множестве , причем при . Тогда несобственный интеграл определяется равенством

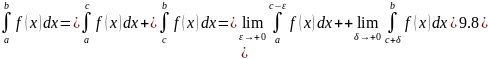
Пример 1. Интеграл сходится при и расходится при .

Доказательство так же, как и в примере 1 п.9.1 использует первообразную степенной функции. При

,

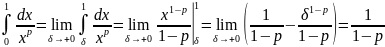т.е. интеграл сходится. Аналогично рассматривается случай и доказывается, что интеграл расходится.◄

Пример 2. Исследовать на сходимость интеграл .

Решение. Подынтегральная функция обращается в бесконечность при . Следовательно

. ◄

Замечание. Для несобственного интеграла (9.8) также вводится главное значение интеграла. А именно, по определению главным значением интеграла (9.8) называется предел

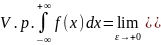. (9.9)

Очевидно также, если интеграл (9.8) сходится, то его значение совпадает с главным значением (9.9). Но возможны ситуации, когда интеграл (9.8) расходится, а главное значение (9.9) – конечно.

Для интеграла (9.7) главное значение можно ввести аналогичным образом.

Для сходящихся несобственных интегралов 2-го рода также справедливы все свойства определённого интеграла.

Сформулируем утверждение для интеграла (9.5), аналогичное теореме 2. Подобные утверждения верны и для остальных интегралов.

Теорема 1.

Если функция непрерывна на интервале – ее первообразная, причем существует конечный предел 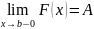, то интеграл (9.5) сходится и равен .

Доказательство, очевидно, также следует из формулы Ньютона-Лейбница. ■

Для положительной подынтегральной функции верны признаки сходимости, аналогичные теоремам, сформулированным для несобственных интегралов 1-го рода.

На практике также в качестве функции сравнения удобно использовать степенную функцию. Это следует из примера 1.

В частности, подынтегральная функция из примера 2 удовлетворяет оценке сверху через степенную функцию с показателем 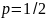, что обеспечивает сходимость интеграла.

Аналогичным образом для функций, принимающих значения любого знака, вводятся понятия абсолютной и условной сходимости и доказываются соответствующие утверждения.

Замечание. Несобственные интегралы могут сразу содержать особенности, присущие интегралам 1-го и 2-го родов. При исследовании сходимости таких интегралов надо «разделять трудности».