Методическое пособие по высшей математике. Второй семестр

А. Б. Алексеев

2022 Г. СПбГут им. Проф. М. А. Бонч-Бруевича Санкт-Петербург, пр. Большевиков, д. 22

Оглавление

9. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ. 2

9.1. Несобственный интеграл 1-го рода. 2

Теорема 1. 4

Теорема 2. 4

Лемма. 4

Теорема 3. 5

Теорема 4. 5

Теорема 5. 7

9.2. Несобственный интеграл 2-го рода. 7

Теорема 1. 10

Литература 12

1. ФУНКЦИИ НЕСКОЛЬКИХ ВЕЩЕСТВЕННЫХ ПЕРЕМЕННЫХ. ОСНОВНЫЕ ПОНЯТИЯ 13

Пример 1.1. Найти частные производные функции 17

Пример 1.2. Найти частные производные второго порядка функции 18

Пример 1.3. В точке найти градиент функции 21

Пример 1.4. В точке найти производную по направлению градиента функции 21

Пример 1.5. Исследовать на экстремум функцию 22

Пример 1.6. В кольце найти наибольшее и наименьшее значения функции 23

2. ДВОЙНОЙ ИНТЕГРАЛ 24

Пример 2.1. Найти объем пирамиды, ограниченной плоскостями 26

9. Несобственные интегралы.

9.1. Несобственный интеграл 1-го рода.

Напомним, что определённый интеграл в основном рассматривался при условии непрерывности функции 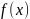на замкнутом конечном интервале 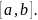Здесь мы рассмотрим вопрос определения интеграла для неограниченных интервалов. Такие интегралы называются несобственными интегралами 1-го рода.

Пусть функция непрерывна на интервале 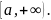Тогда несобственный интеграл 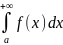определяется равенством

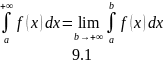
Если предел (9.1) существует и конечен, то говорят, что интеграл сходится, и предел берется за значение интеграла, а если предел не существует или бесконечен, то говорят, что интеграл расходится.

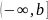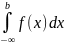Аналогично строится определение несобственного интеграла и для других видов неограниченных интервалов. А именно, пусть функция непрерывна на интервале , тогда несобственный интеграл определяется равенством

Если функция непрерывна на всей оси 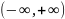, то несобственный интеграл определяется как двойной предел:

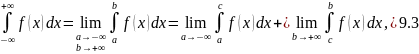
где 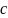– произвольное число.

Пример 1. Интеграл сходится при и расходится при .

Решение. Для 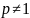найдем первообразную, используя интеграл 1 из таблицы 2, и подставим в формулу Ньютона-Лейбница, тогда

.

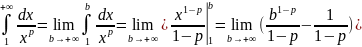Если , то предел конечен 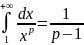и , если 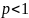, то предел бесконечен и интеграл расходится.

Для 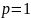первообразная 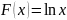стремится к 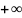при 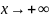. Следовательно, предел бесконечен и интеграл расходится. ◄

Пример 2. Интеграл .

Решение. Воспользуемся первообразной подынтегральной функции, найденной в примере 4 п.7.5. Тогда

. ◄

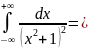
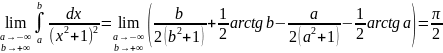Замечание. Для несобственного интеграла (9.3) вводится характеристика, которая называется главным значением интеграла. А именно, по определению главным значением интеграла (9.3) называется предел

Здесь при нахождении предела концы промежутка симметрично уходят на бесконечность. Очевидно, если интеграл (9.3) сходится, то его значение совпадает с главным значением (9.4). Но возможны ситуации, когда интеграл (9.3) расходится, а главное значение (9.4) - конечно.

Пример 3. Интеграл

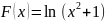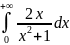Интеграл расходится из-за того, что первообразная стремится к при и каждый из интегралов и 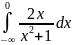расходится, но , т.к. для нечетной подынтегральной функции интеграл по симметричному промежутку 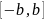равен нулю (см. лемму 2 п.8.5). ◄

Для сходящихся несобственных интегралов справедливы все свойства определённого интеграла.

В дальнейшем утверждения будем формулировать для интегралов вида (9.1), подобные утверждения верны и для интегралов (9.2) и (9.3).