
- •§1. Скалярное произведение в линейных пространствах
- •§2. Ортогональные системы
- •§3. Ряд Фурье
- •§4. Тригонометрические ряды. Задача Штурма-Лиувилля
- •§5. Сходимость ряда Фурье
- •§ 6. Интегральная формула Фурье
- •§ 7. Свойства преобразование Фурье
- •§ 8. Примеры решений индивидуальных заданий
- •§9. Индивидуальные задания
- •Литература
- •Содержание
- •Алексеев Александр Борисович, Попова Наталья Владимировна, Тащиян Григорий Михайлович ряд и интеграл фурье Учебно-методическое пособие
- •191186 СПб., наб. Р. Мойки, 61
§5. Сходимость ряда Фурье
Вопрос
о равенстве значений функции
и суммы
 её ряда Фурье оказался глубоким.
Обсуждение этого вопроса началось с
опубликования в 1804 г. работы Фурье, где
он использовал тригонометрический ряд
для решения уравнения теплопроводности,
и длится до сих пор. Это обсуждение
привело к развитию различных областей
математики. Так в работах
В.А. Стеклова (1900-1910), в частности, был
получен следующий результат
её ряда Фурье оказался глубоким.
Обсуждение этого вопроса началось с
опубликования в 1804 г. работы Фурье, где
он использовал тригонометрический ряд
для решения уравнения теплопроводности,
и длится до сих пор. Это обсуждение
привело к развитию различных областей
математики. Так в работах
В.А. Стеклова (1900-1910), в частности, был
получен следующий результат
Теорема
(Стеклов). Дважды
непрерывно дифференцируемая на множестве
 функция
,
удовлетворяющая
однородному граничному условию
(4.6), разлагается
в абсолютно и равномерно сходящийся
ряд
(4.7) по
собственным функциям данной краевой
задачи.
функция
,
удовлетворяющая
однородному граничному условию
(4.6), разлагается
в абсолютно и равномерно сходящийся
ряд
(4.7) по
собственным функциям данной краевой
задачи.
Напомним,
что ряд Фурье
функции
сходится к этой функции в смысле метрики
пространства
 .
В 1966 г. Л. Карлесон доказал, что равенство
.
В 1966 г. Л. Карлесон доказал, что равенство
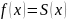 выполняется почти везде (см. замечание
к примеру 3 из §1).
Поэтому, обычно, вместо равенства
пишут
выполняется почти везде (см. замечание
к примеру 3 из §1).
Поэтому, обычно, вместо равенства
пишут
 и говорят, что функции
соответствует ряд Фурье
или функция
имеет ряд Фурье
.
и говорят, что функции
соответствует ряд Фурье
или функция
имеет ряд Фурье
.
Для справедливости равенства в конкретной точке требуется наложить дополнительные условия (условия «гладкости») на функцию . В этом пособии приводится признак Дирихле, который имеет широкое применение в задачах практики.
Определение. Функция называется кусочно-монотонной на промежутке, если этот промежуток можно разложить на конечное число частичных промежутков, внутри которых по отдельности функция монотонна.
Признак
Дирихле.
Если функция
кусочно-монотонна
в промежутке
 и имеет в нём не более
чем
конечное число точек разрыва первого
рода, то её ряд Фурье сходится, причём
и имеет в нём не более
чем
конечное число точек разрыва первого
рода, то её ряд Фурье сходится, причём

где
 и
и
 – пределы
слева и справа в точке
– пределы
слева и справа в точке
 соответственно.
соответственно.
Условия на функцию, высказанные здесь, называются условиями Дирихле.
В силу периодичности гармоник (членов ряда) из сходимости ряда Фурье на промежутке следует его сходимость всюду, т.е. на всей числовой оси. Суммой этого ряда, очевидно, будет 2l-периодическая функция, которую будем обозначать опять . Функция , определенная указанным образом, будет периодическим продолжением .
§ 6. Интегральная формула Фурье
Предположим,
что функция
на каждом конечном отрезке удовлетворяет
условиям Дирихле. Кроме того, предположим,
что функция абсолютно интегрируема на
R,
т.е. несобственный интеграл
 сходится.
сходится.
Пусть
x
– любая точка на числовой оси; выберем
любое число l,
удовлетворяющее условию
 .
Рассмотрим тригонометрический ряд
Фурье функции
в комплексной форме на симметричном
промежутке
:
.
Рассмотрим тригонометрический ряд
Фурье функции
в комплексной форме на симметричном
промежутке
:
 ,
(1)
,
(1)
где
 (2)
(2)
(переменная
интегрирования обозначена символом
 вместо x,
чтобы не путать её с заданной точкой
x).
вместо x,
чтобы не путать её с заданной точкой
x).
Подставляя выражения коэффициентов (2) в ряд (1), получим

Обозначим
 ,
,
 ,
,
 .
.
Т.к.
функция
абсолютно интегрируема на R,
то интегралы
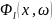 сходятся абсолютно при всех значениях
l.
Последнее
выражение для суммы
сходятся абсолютно при всех значениях
l.
Последнее
выражение для суммы
 можно записать в виде
можно записать в виде
 .
(3)
.
(3)
Это
выражение напоминает "интегральную
сумму" для несобственного интеграла
 ,
где подынтегральная
функция равна
,
где подынтегральная
функция равна
 .
.
В
«интегральной сумме»
ранг дробления стремится к нулю, когда
стремится к нулю, когда
 .
Всё это позволяет надеяться, что в
равенстве (3) можно перейти к пределу
при l→+∞.
Можно доказать, что это действительно
так.
.
Всё это позволяет надеяться, что в
равенстве (3) можно перейти к пределу
при l→+∞.
Можно доказать, что это действительно
так.
В результате получается равенство
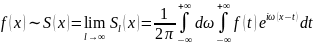 ,
,
которое называется интегральной формулой Фурье или интегралом Фурье.
Теорема. Пусть функция абсолютно интегрируема на R и удовлетворяет условиям Дирихле на каждом конечном промежутке . Тогда интеграл Фурье сходится (в смысле главного значения) и

В дальнейшем будем считать, что функция , удовлетворяющая условиям Дирихле, в точках разрыва удовлетворяет условию
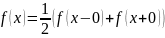 .
.
При таком условии интегральная формула Фурье, для рассматриваемого класса функций, примет вид
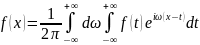 .
(4)
.
(4)
Преобразуем интегральную формулу Фурье. Используя формулу Эйлера, получим


Подынтегральная
функция во втором интеграле является
нечётной по ω,
поэтому интеграл по симметричному
промежутку
 равен 0; что касается первого интеграла,
то его подынтегральная функция –
чётная, поэтому можно интегрировать
только по половине этого промежутка,
но результат удвоить. Поэтому получаем
интегральную формулу Фурье в следующем
виде:
равен 0; что касается первого интеграла,
то его подынтегральная функция –
чётная, поэтому можно интегрировать
только по половине этого промежутка,
но результат удвоить. Поэтому получаем
интегральную формулу Фурье в следующем
виде:
 .
(5)
.
(5)
Вернёмся к интегральной формуле Фурье (4).
Определение. Преобразованием Фурье функции называется функция
 .
.
Из
условий, наложенных на функцию
,
следует, что функция
 непрерывна
на R.
Тогда интегральная
формула Фурье примет вид
непрерывна
на R.
Тогда интегральная
формула Фурье примет вид
 .
.
Поэтому, естественно, вводится понятие обратного преобразования Фурье.
Определение. Обратным преобразованием Фурье функции называется функция
 .
.
Замечание 1. Данное представление функции является аналогом ряда Фурье в комплексной форме (4.1).
Замечание
2. В
этой формуле выражение
 задает, условно говоря, пакет комплексных
гармоник с частотами, непрерывно
распределенными на промежутке
задает, условно говоря, пакет комплексных
гармоник с частотами, непрерывно
распределенными на промежутке
 и
суммарной комплексной амплитудой
и
суммарной комплексной амплитудой
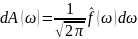 .
Функция
.
Функция
 называется
спектральной
плотностью.
Поэтому интегральную формулу Фурье,
записанную в виде
называется
спектральной
плотностью.
Поэтому интегральную формулу Фурье,
записанную в виде

можно трактовать, как разложение функции в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке
Замечание
3. Обратимся
к интегральной формуле Фурье (5).
Пользуясь тригонометрической формулой
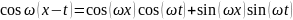 ,
из (5) выводим
,
из (5) выводим
 .
.
Если, по аналогии с формулами (4.3), обозначим

 .
(6)
.
(6)
то получим равенство
 ,
(7)
,
(7)
которое аналогично тригонометрическому ряду Фурье (4.2).
Рассмотрим частные случаи формул (6) и (7).
1.
Пусть функция
является чётной. Тогда в первой из
формул (6) подынтегральная функция
является чётной, а во второй – нечётной.
Поэтому
 =0
при всех ω,
а
=0
при всех ω,
а
 (8)
(8)
В формуле (7) при этом остаётся только первое слагаемое:
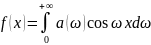 .
(9)
.
(9)
2.
Пусть функция
является нечётной. Тогда в первой из
формул (6) подынтегральная функция
является нечётной, а во второй – чётной.
Поэтому
 =0
при всех ω,
а
=0
при всех ω,
а
 .
(10)
.
(10)
В формуле (7) при этом остаётся только второе слагаемое:
 .
(11)
.
(11)
Заметим,
что в формулах (8) и (10) достаточно, чтобы
функция
была определена только на промежутке
 .
.
Формулы (9) и (11) приводят к следующим определениям преобразований.
Определение. Косинус-преобразованием Фурье функции называется функция
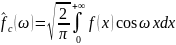 .
(12)
.
(12)
Определение.
Обратным
косинус-преобразованием Фурье
функции
 называется функция
называется функция
 .
(13)
.
(13)
Определение. Синус-преобразованием Фурье функции называется функция
 .
(14)
.
(14)
Определение.
Обратным
синус-преобразованием Фурье
функции
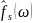 называется функция
называется функция
 .
(15)
.
(15)
Замечание 4. Пары формул (12), (13) и (14), (15) симметричны: прямое и обратное преобразования отличаются только обозначениями функций и переменных.
Замечание 5. Легко проверяются следующие утверждения:
если
функция
чётная, то
 ;
;
если
функция
нечётная то
 .
.
Замечание 6. Кроме того, формулы (9) и (13) дают чётное, а формулы (11) и (15) – нечётное продолжение функции с промежутка (0,+∞) на всю числовую ось (с указанными выше поправками в точках разрыва и в точке x=0).
