8.6. ВЫЧИСЛЕНИЕ ПЛОЩАДИ С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

Как известно (см. (8.6)), к понятию определённого интеграла приводит задача о вычислении площади криволинейной трапеции.

Пример 1. Найти площадь фигуры, ограниченной эллипсом 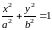с полуосями: и .

рис. 23

Решение. Так как эллипс симметричен относительно осей координат достаточно вычислить площадь четвертой части, и умножить на 4. Получаем (см. пример 1 п.8.5)

. ◄

Нетрудно понять, что площадь фигуры, заключённой между графиками функций , где для , и прямыми (рис. 24а), вычисляется по формуле

(8.25)

а) б)

Рис. 24

Пример 2. Найти площадь фигуры, заключенной между линией и параболой .

Решение. На рисунке 24б представлена фигура, ограниченная указанными линиями.

Для определения граничных точек решая уравнение , получаем . На промежутке Так фигура имеет ось симметрии , то (см. лемму 1 п. 8.5)

◄

Для некоторых областей площадь удобнее вычислять, используя полярные координаты.

Полярными координатами точки на плоскости называется пара чисел , которые характеризуют положение точки относительно полюса и полярной оси. Полярной осью называется числовая полуось на плоскости, то есть полупрямая с масштабом и направлением, а полюсом – крайняя (начальная) точка этой полуоси. Число - расстояние от точки до полюса, а - угол поворота от полярной оси до направления на точку (см. рис. 25). Положительными считаются углы против часовой стрелки. Следовательно, , а . Если точка совпадает с полюсом, то , а может считаться любым.

Рис. 25

Если полюс совпадает с началом декартовой системы координат, а полярная полуось – с положительной полуосью оси (см. рис. 27), то связь между декартовыми и полярными координатами точки выражается формулами:

.

Криволинейным сектором на плоскости (рис. 26) называется фигура, ограниченная двумя лучами, идущими из полюса под углами и , , и кривой, расстояние до точек которой зависит от угла , то есть представляет собой функцию .

Рис. 26

Доказано (см. [2]), что площадь криволинейного сектора вычисляется с помощью интеграла

(8.26)

Пример 3. Найти площадь фигуры, ограниченной линией

.

Решение. Построение этой фигуры можно сделать, накладывая сетку полярной системы на декартову с помощью формул связи. Для построения мы ограничимся простыми рассуждениями. Функция 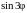имеет период . Достаточно построить линию на промежутке а затем рисунок поворачивать на . При значении . С увеличением угла от до увеличивается от до , а затем от до уменьшается до . На промежутке фигуры нет, так как (см. рис. 27).

Рис.27

В силу симметрии достаточно вычислить - площадь заштрихованной половины лепестка (см. пример 4 п.7.3), а затем умножить ее на шесть:

.

Тогда площадь всей фигуры равна

. ◄

8.7. ВЫЧИСЛЕНИЕ ОБЪЕМА С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

Пусть тело ограничено некоторой поверхностью и плоскостями , причём площадь его сечения плоскостью, перпендикулярной к оси при произвольном равна .

Рис.28

Тогда можно доказать (см. [2]), что объём этого тела вычисляется по формуле

(8.27)

Пример 1. Сечением тела плоскостью, перпендикулярной оси и проходящей через точку с абсциссой является квадрат, сторона которого равна . Найти объем тела.

Решение. Площадь сечения . Тогда объем тела (рис.28)

. ◄

Пример 2. Вычислить объем тела, ограниченного параболоидом и конусом (см. [6]).

Решение. Вершины конуса и параболоида находятся в начале координат. Сечения, перпендикулярные оси и проходящие через точку , для обеих поверхностей являются эллипсами (рис.29).

Рис.29

Для параболоида: , полуоси эллипса . Для конуса: , полуоси эллипса .

Сечение тела представляет собой фигуру, расположенную между двумя эллипсами. Следовательно, площадь сечения (см. пример 1 п.8.6):ц

.

Решив систему уравнений: и , получаем, что поверхности пересекаются при (вершины) и .

Воспользовавшись формулой (8.27), где заменено на , вычислим объем тела

. ◄

Пусть задана криволинейная трапеция, ограниченная графиком функции осью и прямыми Если вращать эту трапецию вокруг оси , то получится тело вращения, объём которого вычисляется по формуле:

. (8.28)

Рис.30

Формула (8.28) является частным случаем формулы (8.27), поскольку (см. рис.30) в поперечном сечении тела вращения – круг, следовательно, .

Пример 3. Вычислить объем тора (рис.31).

Решение. Тор можно представить как фигуру, полученную вращением окружности вокруг прямой, которую примем за ось (рис.32).

Рис.31 Рис.32

Пусть радиус окружности равен , а центр окружности находится от прямой на расстоянии . Объем тора равен разности объемов, полученных от вращения верхней и нижней половин окружности.

Верхняя полуокружность является графиком функции , нижняя полуокружность - график функции .

Тогда

. ◄

8.8. ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

Пусть кривая , заданная в трехмерном пространстве, в каждой точке имеет касательную, непрерывно меняющуюся от точки к точке. (Такие кривые называются гладкими). Разобьем ее на участков точками .

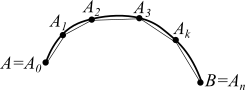
Рис. 33

Обозначим через длину отрезка, соединяющего точки . Тогда длина ломаной (см. рис.33), вписанной в кривую , равна

. (8.29)

Длиной кривой называется конечный предел

, (8.30)

не зависящий от способа разбиения, если ранг разбиения , где

. (8.31)

Можно доказать (см. [2]), что для гладких ограниченных кривых предел (8.30) существует.

Пусть кривая в трехмерном пространстве (см. [6]) задана параметрически, то есть координаты точки на кривой вычисляются как значения функций, зависящих от дополнительной переменной (параметра) , , где функции , имеют непрерывные производные для . Доказано (см. [2]), что длина дуги в этом случае вычисляется по формуле

(8.32)

Для плоской кривой можно считать 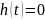, тогда формула (8.32) принимает вид

(8.33)

Пример 1. Вычислить длину одного витка винтовой линии (рис.34) .

Решение. Применяя формулу (8.32), вычисляем

,

.

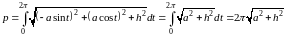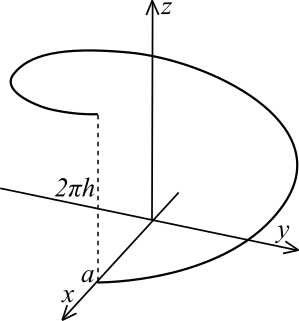
Рис.34 ◄

Если дуга является графиком однозначной функции , то за параметр можно взять переменную . Тогда , и формула (8.33) принимает вид

(8.34)

Пример 2. Вычислить длину дуги параболы от ее вершины до точки (Рис.35).

Решение. Очевидно, что . Применяя формулу (8.34) и пример 5 п.7.5, получаем

. ◄

Рис. 35 рис.36

Пример 3. Вычислить длину астроиды (рис.36, ), кривой, которая задается уравнением .

Решение. В силу симметрии кривой достаточно найти длину участка при , а затем умножить на четыре. Выразим через и найдем производную

.

Тогда

. ◄

Формула, подобная (8.34) получается и в том случае, когда дуга является графиком однозначной функции . Тогда за параметр можно взять переменную . Длина такой дуги вычисляется по формуле

(8.35)

Если кривая описана в полярных координатах, т.е. расстояние до точек кривой от полюса определяется как функция , причем кривая ограничена двумя лучами, идущими из полюса под углами и , , (см. рис.26), то для вычисления длины дуги за параметр можно взять угол . Тогда, используя соотношения

,

из формулы (8.33) получим, что длина дуги вычисляется с помощью интеграла

(8.36)

Пример 4. Вычислить длину кардиоиды .

Решение. Кардиоида представлена на рисунке 32.

Рис. 32

Так как кривая симметрична относительно полярной оси, найдем длину верхней половины и умножим ее на два. Интегрировать в этом случае надо от до . Проведем вычисления

и применим формулу (8.36)

.

Заметим, что при . ◄

Литература

1.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. (В 3-х томах). — М. 2003. т.1— 680с.

2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. (В 3-х томах). — М. 2003. т.2— 864с.

3. Краснов М.Л. Вся высшая математика. Т.1. /М, Л. Краснов, Л. И. Киселев, М. И. Макаренко. – М., 2003, – 328с.

4. Краснов М.Л. Вся высшая математика. Т.2. /М, Л. Краснов, Л. И. Киселев, М. И. Макаренко. – М., 2004, – 192с.

5. Берман Г.Н. Сборник задач по курсу математического анализа. – М., 1985.–384с.

6. Алексеев А.Б., Филиппова А.Ф. Элементы векторной алгебры и аналитической геометрии. Учебно-методическое пособие. СПб ГУТ, 2019,– 46с.