8. Определенный интеграл.
8.1. Определение и свойства
Пусть
функция
принимает конечные значения в любой
точке замкнутого интервала
.
Разобьём
промежуток
точками
на интервалы
.
Обозначим через
длину
-того интервала:
.
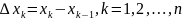В
каждом
-том
интервале выберем произвольную точку
.
Составим
сумму
.
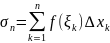(8.1)
Сумма
(8.1) называется интегральной
суммой
для заданной функции
и интервала
.
Введем ранг
разбиения:
,
(8.2)
и
устремим
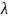к нулю.
Если
при
существует конечный предел у интегральной
суммы (8.1), не зависящий ни от способа
разбиения, ни от выбора точек
,
то он называется определенным
интегралом от функции
по
промежутку
и обозначается
.
Функция называется в этом случае интегрируемой на интервале .
В качестве определения удобно взять следующую формулу:
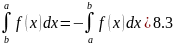(8.3)
А также
.
(8.4)
К понятию определённого интеграла приводят многие физические и геометрические задачи, в частности, задача о вычислении площади криволинейной трапеции.
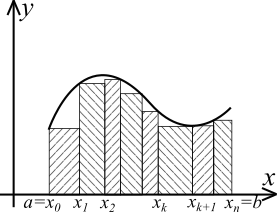
Рассмотрим
фигуру (она называется криволинейной
трапецией),
ограниченную вертикалями
,
осью
и графиком функции
,
принимающей положительные значения и
непрерывной на интервале
.
В этом случае интегральная сумма (8.1)
равна площади ступенчатой (заштрихованной)
фигуры, близкой к криволинейной трапеции
(рис.
20).
Рис. 20
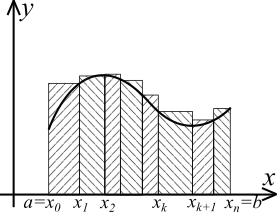
Построим
для данного разбиения еще две суммы:
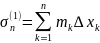и
, где
– наименьшее значение функции
,
а
– наибольшее значение на интервале
.
|
|
Рис. 21.
Очевидно (см. рис. 21) выполнение двух неравенств:
,
,
(8.5)
где
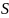- площадь криволинейной трапеции. Легко
видеть, что при
(дроблении на все меньшие интервалы)
сумма
возрастает, оставаясь ограниченной
сверху в силу второго из неравенств
(8.5), а сумма
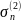убывает, оставаясь ограниченной снизу.
Тогда из теоремы о пределе монотонной
функции п.2.3 следует, что существуют
пределы
и
,
причем
.
Рассмотрим
разность
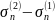и докажем что она стремится к нулю при
.
Тогда из теоремы о пределе суммы следует
равенство пределов
.
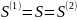Действительно,
зададим число
,
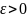построим
.
В силу непрерывности функции
существует число
такое, что при
разность
для любого интервала разбиения. Тогда
.
Следовательно,
в силу первого из неравенств (8.5), по
теореме о «сжатой переменной» п.2.2
существует предел интегральной суммы
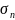и, тем самым, определенный интеграл, и
его значение совпадает с площадью
криволинейной трапеции
.
То есть
.
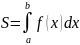(8.6)
■
Мы получили также, что положительная непрерывная функция является интегрируемой. Можно доказать (см. [2]), что интегрируемыми являются и непрерывные, и кусочно-непрерывные функции (т.е. функции, имеющие только конечное число разрывов 1-го рода), принимающие значения любого знака.
Приведем основные свойства определенного интеграла.
1) Так как определенный интеграл представляет собой число, зависящее только от подынтегральной функции и интервала, на котором она задана, то верно равенство
.
То есть определенный интеграл не зависит от обозначения переменной интегрирования. ■
2)
Свойство
линейности.
Пусть функции
и
– интегрируемы на
,
-
числа. Тогда
.
(8.7)
Доказательство этого утверждения следует из определения определенного интеграла и теоремы о пределе суммы. ■
3)
Пусть подынтегральная функция
,
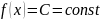тогда
.
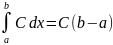(8.8)
Доказательство
формулы (8.8)
следует из того, что в данном случае
интегральная сумма (8.1)
равна
и не зависит ни от
способа разбиения, ни от выбора точек
.
■
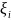Следствие.
В частности, если
,
то
,
если
,
то
.
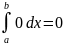4)
Свойство
аддитивности.
Пусть
,
функция
– интегрируема на всех трех интервалах
,
и
.
Тогда
.
(8.9)
Доказательство
этого утверждения также следует из
определения определенного интеграла
и теоремы о пределе суммы, причем в
качестве одной из точек разбиения
следует взять точку
.
■
Следствие. Используя формулы (8.3) и (8.4) можно доказать, что
формула
(8.9)
будет верна при любом расположении
чисел
.