
ИСиТ / 09.03.02 Интеллектуальные информационные системы и технологии / 2 курс 2 семестр / Алексеев Александр Борисович / Высшая математика / Высшая математика / Методички от Алексеева (в порядке посылаемости) / 1сем / 7.6 - 7.8 Методы интегрирования
.docx7.6. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Нахождение первообразных из множества элементарных функций возможно только для некоторых классов функций, в частности, для рациональных дробей (1.8).
Рациональная дробь

называется
правильной,
если степень знаменателя больше степени
числителя, т.е.
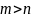 ,
и
неправильной
в противном случае.
,
и
неправильной
в противном случае.
7.6.1. Интегрирование простейших рациональных дробей
Простейшими рациональными дробями называются дроби четырех типов:
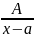 ;
; ;
;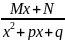 ;
;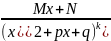 .
.
Здесь
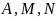 – вещественные числа,
– вещественные числа,
 - натуральное число,
- натуральное число,
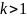 ,
дискриминант
,
дискриминант
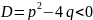 .
.
Дроби 1-го и 2-го типов интегрируются, как показано в примере 2 п. 7.3.
 ,
(7.11)
,
(7.11)
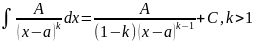 .
(7.12)
.
(7.12)
Дробь 3-го типа интегрируется, как в примере 1 п. 7.4. В результате:
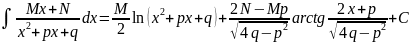 .
(7.13)
.
(7.13)
Для
интегрирования дроби 4-го типа используется
замена
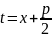 и алгоритм понижения степени знаменателя,
как в примере 4 п. 7.5,
(см.,
например, [2]).
и алгоритм понижения степени знаменателя,
как в примере 4 п. 7.5,
(см.,
например, [2]).
7.6.2. Интегрирование правильных рациональных дробей
Для правильной рациональной дроби верно утверждение: любая правильная дробь раскладывается в сумму простейших дробей (доказательство см. в [2]). ■
Следовательно, для интегрирования правильной дроби ее надо разложить на простейшие и проинтегрировать их.
Алгоритм разложения дроби на простейшие состоит в следующем. Сначала пишут разложение знаменателя дроби на множители, в соответствии с ним - необходимый вид разложения дроби на простейшие с неопределенными коэффициентами, затем находят числовые значения коэффициентов, используя сочетание двух методов: метода подстановки и метода приравнивания коэффициентов при одинаковых степенях переменной.
Пример
1.
Разложить
дробь
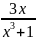 на простейшие.
на простейшие.
Решение.
Знаменатель дроби раскладывается на
множители как сумма кубов:
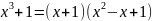 .
Тогда разложение дроби на простейшие
с неопределенными коэффициентами имеет
вид:
.
Тогда разложение дроби на простейшие
с неопределенными коэффициентами имеет
вид:
 .
.
Приведя
к общему знаменателю и приравняв
числители, получим равенство
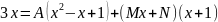 .
Отсюда, подставляя
.
Отсюда, подставляя
 ,
находим коэффициенты
,
находим коэффициенты
 .
Далее, приравняв коэффициенты при
степенях
.
Далее, приравняв коэффициенты при
степенях
 ,
получим
,
получим
 ,
то есть
,
то есть
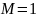 .
Окончательное разложение имеет вид:
.
Окончательное разложение имеет вид:
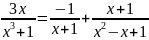 .
◄
.
◄
Рассмотрим пример интегрирования правильной дроби.
Пример
2.
Найти интеграл
 .
.
Решение. Используем разложение подынтегральной дроби на простейшие, полученное в примере 1, и интеграл из примера 1 п. 7.4. Тогда
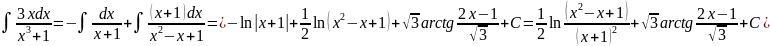 .
◄
.
◄
7.6.3. Интегрирование неправильных рациональных дробей
Для неправильной рациональной дроби имеет место следующая
Теорема (доказательство см. в [2]). Неправильная рациональная дробь представима в виде
 ,
(7.14)
,
(7.14)
где
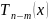 и
и
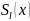 – многочлены степеней
– многочлены степеней
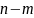 и
и
 соответственно. ■
соответственно. ■
Из формулы (7.14) следует, что интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.
Пример.
Найти интеграл
 .
.
Решение. Проведем деление многочленов в подынтегральной функции, тогда
 .
.
Разложение получившейся правильной дроби на простейшие имеет вид:
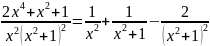 .
.
Тогда, используя таблицу и пример 4 п. 7.5, получим
 .
◄
.
◄
7.7. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
Пусть подынтегральная функция имеет вид
 ,
(7.15)
,
(7.15)
где
 - рациональная функция своих аргументов,
- рациональная функция своих аргументов,
 ,
а
,
а
 - рациональные числа. Тогда, сделав
замену
- рациональные числа. Тогда, сделав
замену
 ,
(7.16)
,
(7.16)
где
 - общий знаменатель всех дробей
, получим интеграл от рациональной дроби
с аргументом
- общий знаменатель всех дробей
, получим интеграл от рациональной дроби
с аргументом
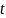 .
.
Доказательство.
В
этом случае показатели степени
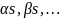 являются
целыми числами.
Из
равенства (7.16) следует, что
являются
целыми числами.
Из
равенства (7.16) следует, что
 .
.
Тогда при подстановке в (7.15) получаем рациональную функцию от аргумента . ■
Пример.
Найти интеграл
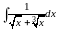
Решение.
Замена (7.16)
в этом случае имеет вид
 .
.
 ◄
◄
Примеры интегрирования других иррациональных выражений см. в [2].
7.8. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Пусть подынтегральная функция имеет вид
 ,
(7.17)
,
(7.17)
где - рациональная функция своих аргументов. Тогда замена
 (7.18)
(7.18)
приводит к интегралу от рациональной дроби с аргументом .
Доказательство.
Так
как
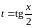 ,
то
,
то
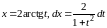 .
Функции синус и косинус выражаются
через тангенс половинного угла по
формулам:
.
Функции синус и косинус выражаются
через тангенс половинного угла по
формулам:
 .
.
Следовательно, при подстановке в (7.17) получаем новую рациональную функцию от аргумента . ■
Пример
1.
Найти интеграл
 .
.
Решение. Сделаем замену
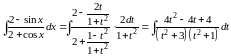 .
.
Разложение дроби на простейшие имеет вид

Приведя к общему знаменателю, получаем
 .
.
Сравним коэффициенты при одинаковых степенях:

Следовательно,
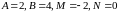 .
.

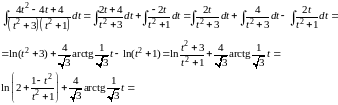
Подставляя , получаем
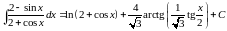 .
◄
.
◄
Для
подынтегральной функции
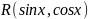 ,
обладающей некоторой симметрией,
возможна другая, более простая, замена
переменной. В частности, возможны
следующие варианты.
,
обладающей некоторой симметрией,
возможна другая, более простая, замена
переменной. В частности, возможны
следующие варианты.
1.
Если,
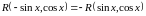 то
подстановка
то
подстановка
 .
.
2.
Если
 то
подстановка
то
подстановка
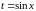 .
.
3.
Если
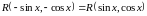 то
подстановка
то
подстановка
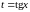 (или
(или
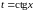 ).
).
Пример
2.
Найти интеграл
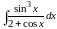 .
.
Решение. Так как сделаем подстановку
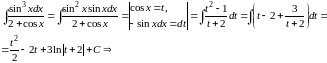
 ◄
◄
Пример
3.
Найти интеграл
 .
.
Решение.
Так как
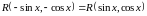 сделаем подстановку
сделаем подстановку
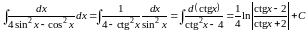 .
◄
.
◄
