- •4.3. Производные высших порядков
- •4.4. Правило лопиталя
- •5. Исследование функций
- •5.1. Теоремы о дифференцируемых функциях
- •5.2. Возрастание, убывание, экстремумы функции
- •5.3. Выпуклость, вогнутость, точки перегиба функции
- •5.4. Асимптоты графика функции
- •5.5. Схема исследования функции и построение ее графика
5.3. Выпуклость, вогнутость, точки перегиба функции
Напомним
определение:
функция
 ,
называется выпуклой
(вогнутой),
если её график расположен ниже (выше)
любой касательной к графику функции
(см. рисунки 8 и 17). Приведённое определение
предполагает дифференцируемость функции
в точках
,
т.к. существование касательной равносильно
существованию производной
(геометрический смысл производной).
,
называется выпуклой
(вогнутой),
если её график расположен ниже (выше)
любой касательной к графику функции
(см. рисунки 8 и 17). Приведённое определение
предполагает дифференцируемость функции
в точках
,
т.к. существование касательной равносильно
существованию производной
(геометрический смысл производной).
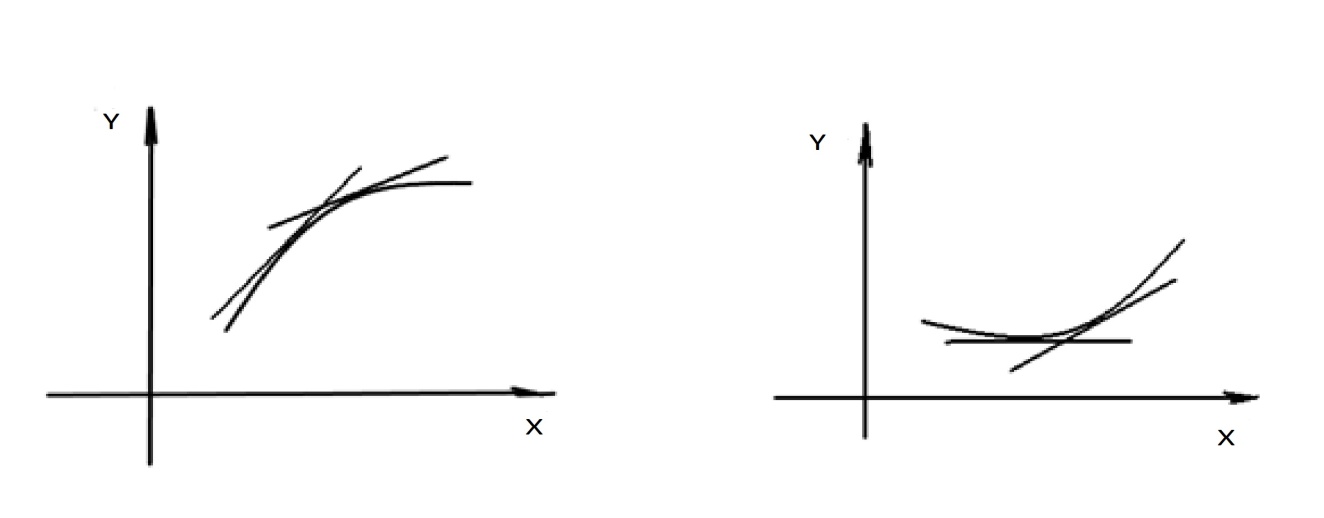 Рис.
17
Рис.
17
Теорема (Достаточный признак выпуклости (вогнутости) функции).
Пусть
функция
при
имеет вторую производную
 ,
причем
,
причем
 (
( ).
Тогда
выпукла (
вогнута) на этом промежутке.
).
Тогда
выпукла (
вогнута) на этом промежутке.
Доказательство.
Пусть
 ,
,
 .
Проведем касательную к графику функции
в точке
:
.
Проведем касательную к графику функции
в точке
:
 .
Обозначим для удобства через
.
Обозначим для удобства через
 значение ординаты
значение ординаты
 на касательной в точке
и рассмотрим
на касательной в точке
и рассмотрим
 .
.
К
разности
 применим формулу (5.5), считая
применим формулу (5.5), считая
 .
Тогда
.
Тогда
 .
.
Аналогично,
применяя формулу (5.5) к разности
 ,
получим
,
получим
 ,
,
где
 .
.
Следовательно,
если
 ,
то график функции
в точке
ниже касательной, если
,
то график функции
в точке
ниже касательной, если
 ,
то график выше касательной. ◄
,
то график выше касательной. ◄
Теорема (Достаточное условие существования точек перегиба).
Пусть функция непрерывна в точке и некоторой ее окрестности. Пусть в этой окрестности существует вторая производная за исключением, быть может, самой точки . Если при переходе через точку производная меняет знак, то - точка перегиба.
Доказательство следует из теоремы о выпуклости (вогнутости) функции). ◄
5.4. Асимптоты графика функции
Наклонная
асимптота
 возможна при стремлении
или
возможна при стремлении
или
 .
Можно доказать (см.
[..]),
что асимптота на
.
Можно доказать (см.
[..]),
что асимптота на
 существует, если существуют конечные
пределы
существует, если существуют конечные
пределы
 .
(5.7)
.
(5.7)
Аналогично при .
Вертикальная
асимптота существует только в той точке
 ,
в какой хотя бы один из односторонних
пределов бесконечен, то есть
,
в какой хотя бы один из односторонних
пределов бесконечен, то есть
 (5.8)
(5.8)
или
 .
(5.9)
.
(5.9)
5.5. Схема исследования функции и построение ее графика
Исследование функции удобно проводить по схеме, разделенной на три этапа, после чего строится график этой функции.
1 Первый этап – анализ свойств самой функции – состоит из следующих пунктов:
11область определения и область значений функции;
12четность, нечетность, периодичность функции;
13точки пересечения графика с осями;
14промежутки знакопостоянства функции;
15поведение на границе области определения и наличие асимптот.
2 Второй этап – анализ свойств первой производной функции – содержит следующие пункты:
21область определения ;
21промежутки знакопостоянства и корни , а также точки, где не существует, что позволяет определить промежутки монотонности и экстремумы функции .
3 Третий этап – анализ свойств второй производной функции – аналогично содержит пункты:
31область определения ;
32 промежутки знакопостоянства и корни , а также точки, где не существует, что позволяет определить промежутки выпуклости, вогнутости и точки перегиба функции .
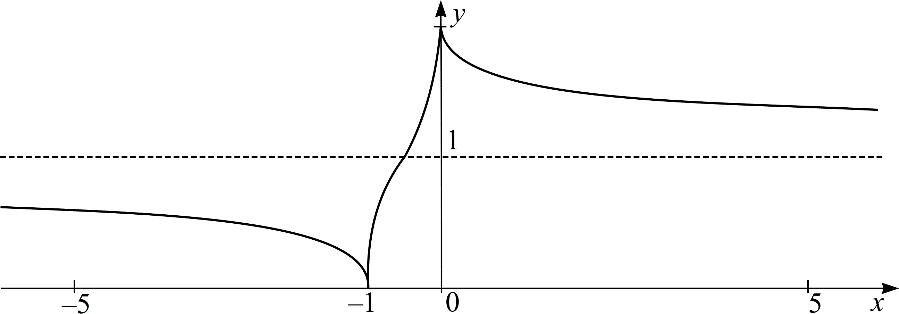
Пример.
Построить график функции
 .
.
Решение. Будем исследовать функцию, нанося на координатную плоскость получаемые при исследовании точки (рис. 18а).
1.
Область
определения функции
 .
Вертикальных асимптот нет.
.
Вертикальных асимптот нет.
Функция не обладает свойствами периодичности, четности, нечетности.
Точки
пересечения с осями: ,
,
 .
Отметим эти точки на координатной
плоскости.
.
Отметим эти точки на координатной
плоскости.
Для
отыскания наклонных асимптот вычислим
значения
 и
и
 :
:


Следовательно,
прямая
 – горизонтальная асимптота, причем
график функции стремится к этой линии
и при
– горизонтальная асимптота, причем
график функции стремится к этой линии
и при
 ,
и при
,
и при
 .
.
2.
Находим производную и определяем экстремумы, промежутки монотонности:
 .
.
Нет
точек, в которых первая производная
обращается в нуль. Однако при значениях
 производная не существует, и эти точки
могут оказаться экстремумами. Отмечаем
знаки производной на полученных
промежутках:
производная не существует, и эти точки
могут оказаться экстремумами. Отмечаем
знаки производной на полученных
промежутках:
![]()
Функция
убывает на промежутках:
 ,
возрастает на промежутке
,
возрастает на промежутке
 .
При
.
При
 у функции острый минимум, при
у функции острый минимум, при
 – острый максимум. Вычислив значения
минимума и максимума, отметим точки:
и
– острый максимум. Вычислив значения
минимума и максимума, отметим точки:
и
 .
.
3.
Вычисляем вторую производную
 .
.
Вторая
производная не существует при значениях
и равна нулю, если
 :
:

На
промежутках:
 функция выпукла вверх, а на промежутках
функция выпукла вверх, а на промежутках
 – выпукла вниз. Точка
– выпукла вниз. Точка
 –
точка перегиба,
–
точка перегиба,
 .
.
Соединив полученные точки, и используя данные о монотонности и выпуклости получаем график функции на рисунке 18б. ◄
|
|
а) б)
Рис. 18