
- •4.3. Производные высших порядков
- •4.4. Правило лопиталя
- •5. Исследование функций
- •5.1. Теоремы о дифференцируемых функциях
- •5.2. Возрастание, убывание, экстремумы функции
- •5.3. Выпуклость, вогнутость, точки перегиба функции
- •5.4. Асимптоты графика функции
- •5.5. Схема исследования функции и построение ее графика
4.3. Производные высших порядков
Пусть
в открытом интервале, содержащем точку
 ,
существует
первая производная
функции
,
существует
первая производная
функции
 .
.
Второй
производной
 в точке
функции
называется производная от её первой
производной:
в точке
функции
называется производная от её первой
производной:
 .
.
Третьей производной в точке функции называется производная от её второй производной:
 .
.
Аналогичным
образом строится определение производных
высоких порядков, причем производные
порядка
 ,
начиная с четвёртого, принято обозначать
символом
,
начиная с четвёртого, принято обозначать
символом
 .
Все они определяются формулой
.
Все они определяются формулой
 .
(4.13)
.
(4.13)
Из результатов п. 4.2.2 получаются свойства производных – го порядка:
1)
 ;
;
2)
 ;
;
3)
 ,
,
где
 – биномиальные коэффициенты.
– биномиальные коэффициенты.
В частности,
 ;
;
 .
.
Пример.
Найти производную порядка
 для функции
для функции
 .
.
Решение. Вычислим последовательно производные первого порядка, второго и далее:

 .
◄
.
◄
Полученную формулу строго можно доказать методом математической индукции.
4.4. Правило лопиталя
Производные
можно применять для раскрытия
неопределенностей вида
 и
и
 .
.
Теорема (правило Лопиталя).
Пусть
предел
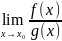 является неопределённостью вида
или
,
причём функции
является неопределённостью вида
или
,
причём функции
 и
и
 дифференцируемы в окрестности точки
дифференцируемы в окрестности точки
 кроме, быть может, самой точки
,
и
кроме, быть может, самой точки
,
и
 .
Пусть существует предел
.
Пусть существует предел
 .
Тогда существует и предел
,
причём
.
Тогда существует и предел
,
причём
 .
(4.14)
.
(4.14)
Доказательство правила Лопиталя следует из теоремы Коши (см. п. 5.1).
Аналогичное
утверждение верно и при
 .
◄
.
◄
Замечание.
Если
и предел
является неопределённостью вида
или
,
и функции
 удовлетворяют условиям теоремы, то
можно опять применить правило Лопиталя,
т.е.
удовлетворяют условиям теоремы, то
можно опять применить правило Лопиталя,
т.е.
 .
.
Примеры.
1)
Найти предел
 .
.
Решение. Вычисляем с помощью правила Лопиталя
 .
◄
.
◄
2)
Найти пределы
 .
.
Решение.
Очевидно, что пределы являются
неопределенностями
 . Применим правило Лопиталя
. Применим правило Лопиталя

При
вычислении предела снова получили
неопределенность
 Применяем правило Лопиталя, пока степень
в знаменателе не станет нулевой или
отрицательной, и получаем
Применяем правило Лопиталя, пока степень
в знаменателе не станет нулевой или
отрицательной, и получаем
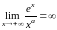 .
.
Итак
можно сравнить при
 важные бесконечно большие функции:
важные бесконечно большие функции:
 и
и
 . Функция
. Функция
 более
высокого порядка, чем
,
более
высокого порядка, чем
, более
высокого порядка, чем
,
а
следовательно, и чем
.
◄
более
высокого порядка, чем
,
а
следовательно, и чем
.
◄
Замечание. В теореме утверждается, что из существования предела следует существование предела и их равенство. Но возможно, что предел не существует, а предел существует.
Например,
предел отношения функций
 и
и
 существует (см. пример 4 на стр. 17)
существует (см. пример 4 на стр. 17)
 .
.
Но
предел отношения производных
 и
и
 не существует в силу колебаний функции
не существует в силу колебаний функции
 .
◄
.
◄
5. Исследование функций
Главную роль при исследовании поведения функции и построении ее графика играет производная этой функции. Основные моменты исследования опираются на следующие теоремы.
5.1. Теоремы о дифференцируемых функциях
Теорема Ферма.
Пусть
функция
непрерывна на замкнутом интервале
 и дифференцируема внутри этого интервала,
т.е. при
и дифференцируема внутри этого интервала,
т.е. при
 .
Пусть в некоторой внутренней точке
.
Пусть в некоторой внутренней точке
 функция
достигает своего наибольшего или
наименьшего значения. Тогда в этой точке
первая производная функции равна нулю,
т.е.
функция
достигает своего наибольшего или
наименьшего значения. Тогда в этой точке
первая производная функции равна нулю,
т.е.
 .
.
Доказательство. Для определённости рассмотрим случай наибольшего значения. Так как функция достигает своего наибольшего значения во внутренней точке , то точка является точкой локального максимума. Докажем, что в точке производная функции равна нулю. Напомним, что
 .
.
Поскольку
 - точка максимума функции
,
то
- точка максимума функции
,
то

а)
Пусть
 Тогда
Тогда
 и переходя к пределу при
и переходя к пределу при
 ,
получим (см. п.2.2, теорема о пределах №7),
что
,
получим (см. п.2.2, теорема о пределах №7),
что

б)
Пусть
 .
Тогда
.
Тогда
 и, следовательно, (та же теорема),
и, следовательно, (та же теорема),

Так
как производная
 существует, из равенства (4.4) следует,
что полученные неравенства выполняются
только в случае
существует, из равенства (4.4) следует,
что полученные неравенства выполняются
только в случае

Случай наименьшего значения рассматривается аналогично. ◄
Теорема Ролля.
Пусть
функция
непрерывна на замкнутом интервале
и дифференцируема внутри этого интервала,
т.е. при
,
причём
 Тогда существует такая точка
,
что
Тогда существует такая точка
,
что
Доказательство.
1)
Если функция
 ,
то её производная равна нулю (см. (4.3)) в
любой точке
.
,
то её производная равна нулю (см. (4.3)) в
любой точке
.
2) Если функция - не константа, то в силу равенства значений функции на концах по теореме Вейерштрасса существует такая внутренняя точка , что значение является наибольшим или наименьшим значением функции на интервале .
Для доказательства теоремы остается сослаться на теорему Ферма. ◄
Теорема Лагранжа.
Пусть функция непрерывна на интервале и дифференцируема внутри этого интервала. Тогда существует такая точка , что
 (5.1)
(5.1)
или
 .
(5.2)
.
(5.2)
Доказательство.
Введём функцию

где
 .
Нетрудно заметить, что
.
Нетрудно заметить, что
 .Тогда
по теореме Ролля существует такая точка
,
что
.Тогда
по теореме Ролля существует такая точка
,
что
 .
Но
.
Но
 .
Следовательно,
.
Следовательно,
 ,
откуда
,
откуда
 .
◄
.
◄
Геометрический смысл теоремы Ролля заключается в том, что если дифференцируемая функция на концах интервала принимает равные значения, то хотя бы в одной точке интервала касательная к графику функции горизонтальна, а геометрический смысл теоремы Лагранжа – в том, что хотя бы в одной точке интервала касательная к графику функции параллельна секущей, проходящей через концы графика (см. рис. 16).


Рис. 16
Замечание. Для равенство (5.2) можно написать в виде:
 ,
(5.3)
,
(5.3)
где
точка
 .
Для
.
Для
 из равенства (5.2) также следует, что
из равенства (5.2) также следует, что
 ,
(5.4)
,
(5.4)
где
точка
 .
Введя число
.
Введя число
 ,
формулы (5.3) и (5.4) можно записать в виде
одной формулы
,
формулы (5.3) и (5.4) можно записать в виде
одной формулы
 ,
(5.5)
,
(5.5)
которую называют формулой конечных приращений.
Теорема Коши.
Пусть
функции
и
 непрерывны
на интервале
и дифференцируемы внутри этого интервала,
причем
непрерывны
на интервале
и дифференцируемы внутри этого интервала,
причем
 Тогда существует такая точка
,
что
Тогда существует такая точка
,
что
 (5.6)
(5.6)
Доказательство.
Как и при доказательстве теоремы Лагранжа, введем функцию
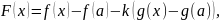
где
 ,
удовлетворяющую условиям теоремы Ролля.
Повторив далее доказательство теоремы
Лагранжа, приходим к формуле (5.6). ◄
,
удовлетворяющую условиям теоремы Ролля.
Повторив далее доказательство теоремы
Лагранжа, приходим к формуле (5.6). ◄
Замечание.
Теорема Лагранжа является частным
случаем теоремы Коши при

