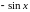Оглавление
4. ПРОИЗВОДНАЯ ФУНКЦИИ 1
4.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ И ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ 1
4.2. СВОЙСТВА ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ И ПРОИЗВОДНЫХ 3
4.2.1. Непрерывность дифференцируемой функции 3
4.2.2. Арифметические действия над дифференцируемыми функциями 4
4.2.3. Производная обратной функции 5
4.2.4. Производная сложной функции 5
4.2.5. Таблица производных 5
4.2.6. Производная степенно-показательной функции 7
4.2.7. Производная функции, заданной параметрически 8
4.2.8. Производная функции, заданной неявно 8
4. ПРОИЗВОДНАЯ ФУНКЦИИ
4.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ И ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Пусть
в открытом интервале, содержащем точку
 ,
задана функция
,
задана функция
 .
Придадим аргументу
достаточно малое приращение
.
Придадим аргументу
достаточно малое приращение
 ,
чтобы точка
,
чтобы точка
 не вышла за пределы интервала. Для
функции получим приращение
не вышла за пределы интервала. Для
функции получим приращение
 .
(4.1)
.
(4.1)
Если существует конечный предел
 ,
(4.2)
,
(4.2)
то
он называется производной
функции
 в точке
и обозначается
в точке
и обозначается
 (или
(или
 ).
).

Рис. 14
Производная
функции
 в точке
в точке
 равна тангенсу угла наклона касательной
(геометрический
смысл производной),
проведённой к графику функции в этой
точке, что хорошо видно на рисунке 14.
равна тангенсу угла наклона касательной
(геометрический
смысл производной),
проведённой к графику функции в этой
точке, что хорошо видно на рисунке 14.
Уравнение
касательной в точке
 имеет вид
имеет вид
 ,
,
где
 .
.
Так
как производная равна пределу отношения
изменения функции ( )
к изменению аргумента (
),
производная
характеризует скорость изменения
функции
в
точке
,
аналогично мгновенной скорости в физике.
)
к изменению аргумента (
),
производная
характеризует скорость изменения
функции
в
точке
,
аналогично мгновенной скорости в физике.
Пример
4.1.
Для функции
 производная
производная
 в любой точке. Это следует из того, что
в любой точке. Это следует из того, что
 .
◄
.
◄
Пример
4.2.
Найти производную функции
 .
.
Решение.
Запишем отношение
 и применим для вычисления предела
эквивалентные величины из п. 2.6.
Тогда
и применим для вычисления предела
эквивалентные величины из п. 2.6.
Тогда
 .
◄
.
◄
Также из определения производной (4.2) следует
Теорема
1.
Пусть
 .
Тогда в любой точке
производная
.
Тогда в любой точке
производная
 .
.
Доказательство.
Очевидно,
что в любой точке
приращение функции
 и, следовательно,
и, следовательно,
 .
(4.3)
.
(4.3)
Операция
нахождения производной
функции называется дифференцированием.
Если
в точке
существует производная
 ,
то функция
,
то функция
 называется дифференцируемой
в
этой точке.
называется дифференцируемой
в
этой точке.
Через
односторонние пределы можно ввести
односторонние
производные
 – производная
слева
в точке
и
– производная
слева
в точке
и
 - производная
справа
в точке
.
Из теоремы 4 (об односторонних пределах)
п. 2.3,
следует
- производная
справа
в точке
.
Из теоремы 4 (об односторонних пределах)
п. 2.3,
следует
Теорема 2. Для существования производной в точке необходимо и достаточно, чтобы в этой точке существовали и были равны односторонние производные, то есть
 .
(4.4)
.
(4.4)
Пример
4.3.
Производная функции
 равна 1 при
равна 1 при
 ,
равна –1 при
,
равна –1 при
 и не существует в
точке
и не существует в
точке
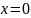 .
◄
.
◄
Если какая-то из односторонних производных в точке равна бесконечности, это значит (см. геометрический смысл производной), что касательная при приближении к этой точке становится вертикальной.
Пример
4.4. Найдем
производную
функции
 .
.
Если
 ,
то
,
то

Для
 .
.
Для
 .
.
Если
 ,
то
,
то
 ,
если
,
если
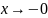 ,
то
,
то
 (см.
рис.15).
(см.
рис.15).
|
|
Рис.15
4.2. СВОЙСТВА ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ И ПРОИЗВОДНЫХ
4.2.1. Непрерывность дифференцируемой функции
Теорема. Если функция дифференцируема в точке , то она непрерывна в этой точке.
Доказательство.
Из существования конечного предела (4.2) и теоремы 2 из п. 2.1 следует, что
 ,
(4.5)
,
(4.5)
где
 при
при
 .
Следовательно
.
Следовательно
 .
(4.6)
.
(4.6)
Тогда
 при
и остается сослаться на (3.2).
◄
при
и остается сослаться на (3.2).
◄
Замечание. Обратное неверно. То есть из непрерывности функции не следует существования её производной. Например, функция непрерывна на всей числовой оси, но в точке у неё нет производной.
4.2.2. Арифметические действия над дифференцируемыми функциями
Приведем свойства производных, связанные со сложением, умножением и делением дифференцируемых функций.
Пусть
функции
и
 - дифференцируемы в точке
,
- дифференцируемы в точке
,
 .
Тогда верны следующие формулы.
.
Тогда верны следующие формулы.

Доказательство 1-ой приведено выше (см. (4.3)). Остальные доказательства опираются на теоремы о пределах и теорему из п. 4.2.1. Приведем для примера
Доказательство
4-ой.
Зададим приращение аргумента
 и найдем приращение функции
и найдем приращение функции
 :
:
 .
.
Используем формулу (4.6). Тогда
 .
.
Здесь
и
 при
.
Разделим на
и устремим
.
Тогда
при
.
Разделим на
и устремим
.
Тогда
 ,
,
т.к.
 в силу непрерывности функции
в силу непрерывности функции
 .
◄
.
◄
4.2.3. Производная обратной функции
Теорема.
Если
 -
обратимая
дифференцируемая функция,
то обратная
функция
-
обратимая
дифференцируемая функция,
то обратная
функция
 тоже является дифференцируемой
функцией, причем производные
взаимно-обратных функций
в точках
тоже является дифференцируемой
функцией, причем производные
взаимно-обратных функций
в точках
 связанных соотношениями
и
,
удовлетворяют равенству
связанных соотношениями
и
,
удовлетворяют равенству
 .
(4.7)
.
(4.7)
Доказательство.
Отношение приращений
и
 может быть записано двояко:
может быть записано двояко:
 .
.
Так как из стремления одного из них к нулю следует стремление к нулю второго, при переходе к пределу получаем формулу (4.7). ◄
Следствие. Из этой теоремы, в частности, следует, что производные взаимно-обратных функций не равны нулю.
Пример
4.5.
Найти производную функции
 .
.
Решение.
Функции
 и
и
 – взаимно-обратные. Тогда из формулы
(4.7)
и примера 4.2
следует,
что
– взаимно-обратные. Тогда из формулы
(4.7)
и примера 4.2
следует,
что
 .
◄
(4.8)
.
◄
(4.8)
4.2.4. Производная сложной функции
Теорема.
Если функция
 – дифференцируема
в точке
,
а функция
– дифференцируема
в точке
,
а функция
 –
дифференцируема в точке
–
дифференцируема в точке
 ,
где
,
где
 ,
то сложная
функция
,
то сложная
функция
 – тоже
дифференцируема
в точке
,
причем
– тоже
дифференцируема
в точке
,
причем
 .
(4.9)
.
(4.9)
Доказательство.
Зададим приращение
,
вследствие этого получим приращения
 и
.
Тогда отношение приращений
и
может быть представлено в виде
и
.
Тогда отношение приращений
и
может быть представлено в виде
 .
.
Устремим
.
Тогда
 ,
,
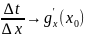 и
и
 .
◄
.
◄
Пример
4.6.
Найти производную функции
 .
.
Решение.
Введем функцию
 и применим формулы (4.8)
при
и применим формулы (4.8)
при
 и (4.9). Тогда, используя пример 4.3,
получим
и (4.9). Тогда, используя пример 4.3,
получим
 .
◄
(4.10)
.
◄
(4.10)
4.2.5. Таблица производных
На основании вышеприведенных свойств можно найти производные всех основных элементарных функций. Они приведены в таблице 1.
Таблица 1
|
|
|
|
|
|
1. const |
0 |
7.
|
|
13. |
|
2.
|
|
8. |
|
14.
|
|
3.
|
|
9.
|
|
15. |
|
4.
|
|
10.
|
|
16. |
|
5.
|
|
11.
|
|
17. |
|
6.
|
|
12.
|
|
18.
|
|
Примеры.
1) Найти производную функции
 .
.
Решение.
Записав
 и используя формулы для производных
суммы и отношения функций, а также из
таблицы формулы 2,3,7, получаем
и используя формулы для производных
суммы и отношения функций, а также из
таблицы формулы 2,3,7, получаем

 ◄
◄
2)
Найти производную функции
 в точке
в точке
 .
.
Решение.
Представив
 ,
получаем
,
получаем
 .
Подставив
,
получаем ответ
.
Подставив
,
получаем ответ
 .
◄
.
◄
4)
Найти производную функции
 .
.
Решение.
Используем формулу (4.9) для производной
сложной функции (внешняя функция –
степенная, а внутренняя:
 ).
Тогда
).
Тогда
 .
◄
.
◄
5)
Найти производную функции
 .
.
Решение. Здесь в построении сложной функции участвуют 4 табличных. Начинаем дифференцировать с внешней (квадратичной). Окончательно получим
 .
◄
.
◄
6)
Найти производную функции

Решение. Применяя формулу дифференцирования суммы функций, а затем вычисляя производную каждого слагаемого как сложной функции, получаем
 ◄
◄
4.2.6. Производная степенно-показательной функции
Степенно-показательной
называется
функция вида
 .
Запишем ее в виде
.
Запишем ее в виде
 и продифференцируем как сложную функцию
и продифференцируем как сложную функцию
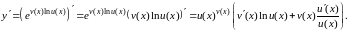
Раскрыв скобки, получаем
 (4.11)
(4.11)
Первое
слагаемое соответствует дифференцированию
показательной функции ( рассматривается как постоянная), второе
– степенной (
рассматривается как постоянная), второе
– степенной ( рассматривается
как постоянная).
рассматривается
как постоянная).
Мы
применяли формулу
 .
Но (4.11)
можно получить другим способом:
прологарифмировав обе части выражения
.
Но (4.11)
можно получить другим способом:
прологарифмировав обе части выражения

 ,
,
найдем производные левой и правой частей
 .
.
Отсюда легко получается (4.11).
Пример
4,7. Найти
производную функции

Решение. Воспользуемся формулой (4.11). Тогда
 .
◄
.
◄
4.2.7. Производная функции, заданной параметрически
Теорема.
Пусть
функция
 задана параметрически,
то есть
на некотором промежутке
задана параметрически,
то есть
на некотором промежутке
 заданы дифференцируемые функции
заданы дифференцируемые функции
 ,
определяющие зависимость
между переменными
и
,
определяющие зависимость
между переменными
и
 ,
причем
,
причем
 .
Тогда для переменной
как функции от
верна формула
.
Тогда для переменной
как функции от
верна формула
 .
(4.12)
.
(4.12)
Доказательство. Отношение приращений и может быть записано так
 .
.
Перейдем к пределу при и получим формулу (4.12). ◄
Замечание.
Производная
 существует, если
.
Это условие обеспечивает существование
обратной функции
существует, если
.
Это условие обеспечивает существование
обратной функции
 .
.
Пример.
Найти производную для функции
 .
.
Решение.
Из формулы (4.12) следует, что
 ◄
◄
4.2.8. Производная функции, заданной неявно
Дифференцирование неявно заданной функции выполняется с учетом того, что одна из переменных, входящих в уравнение, задающее функцию, является независимой, а другая зависимой.
Пример.
Найти производную
 ,
если
,
если
 .
.
Решение.
Считая переменную
независимой
переменной,
а
 функцией от
функцией от
 ,
продифференцируем заданное уравнение:
,
продифференцируем заданное уравнение:
 .
.
Найдем
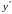 ,
решив полученное линейное уравнение
,
решив полученное линейное уравнение
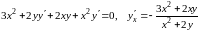 .
◄
.
◄
Замечание.
Проделаем
те же операции, считая переменную
аргументом, а
функцией от

 ,
,
 .
.
Очевидно,
 ,
так как функции
,
так как функции
 и
и
 взаимообратные.
взаимообратные.