Оглавление

2.5. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ 1

2.6. ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ 2

2.7. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО БОЛЬШИХ 3

3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ 3

3.1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 3

3.2. ФУНКЦИИ, НЕПРЕРЫВНЫЕ НА МНОЖЕСТВЕ, И ИХ СВОЙСТВА 5

3.3. КЛАССИФИКАЦИЯ РАЗРЫВОВ 5

2.5. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ

Для сравнения бесконечно малых при 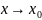используется предел их отношения.

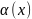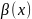Бесконечно малые и называются бесконечно малыми одного порядка,если

.

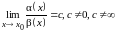В частности, если

,

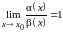то и называются эквивалентными.

Обозначение: .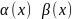

Если

,

то называется бесконечно малой высшего порядка по сравнению с бесконечно малой .

Обозначение: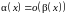 при Читается: есть - малое по сравнению с при .

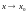Если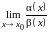 не существует, то бесконечно малые и не сравнимы между собой.

Для бесконечно малых верны следующие свойства.

1. Если 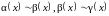, то .

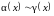2. Пусть 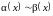. Тогда 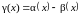– бесконечно малая высшего порядка по сравнению с каждой из них:

.

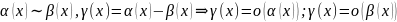3. Если 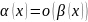, то .

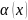
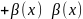4. Если 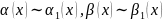, то

.

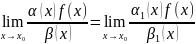Другими словами, если под знаком предела бесконечно малая входит как сомножитель в некоторое выражение, то ее можно заменить на ей эквивалентную. Это утверждение называется принципом эквивалентности.

2.6. ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ

На основании замечательных пределов можно составить таблицу эквивалентных бесконечно малых при .

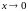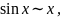
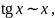
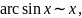
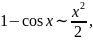
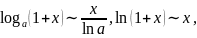
Заметим, что слева от знака эквивалентности стоят различные функции, а справа степенная функция.

Таблица эквивалентных бесконечно малых, их свойства и теоремы о пределах используются для нахождения пределов.

Примеры:

1) ,

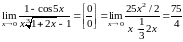2) .

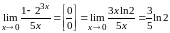Если при вычислении пределов с неопределенностью 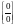переменная стремится к числу, отличному от нуля, то для возможности использовать таблицу, сначала необходимо сделать замену переменной.

Примеры:

.

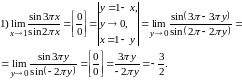
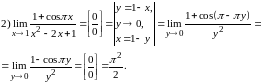2.7. КЛАССИФИКАЦИЯ БЕСКОНЕЧНО БОЛЬШИХ

Для сравнения бесконечно больших также используется предел их отношения. Не останавливаясь подробно, заметим, что определения бесконечно больших одного порядка, эквивалентных и принцип эквивалентности сохраняются.

В частности, многочлен при 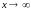эквивалентен своему старшему члену, т.е.

.

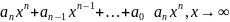Следовательно,

.

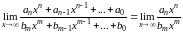После сокращения степеней получаем один из следующих ответов: .

Аналогично находятся пределы и для выражений, содержащих дробные степени.

Пример. Найти .

Решение. Выделив старшие степени в числителе и знаменателе, получим

. ◄

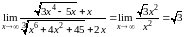3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ

3.1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ

Функция 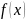называется непрерывной в точке 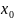, если она определена в этой точке, ее окрестности и

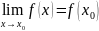. (3.1)

То есть для непрерывной функции возможен переход к пределу под знаком функции. Справедлива следующая очевидная

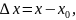
Теорема. Пусть . Функция непрерывна в точке тогда и только тогда, когда

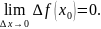(3.2)

Другими словами функция непрерывна в точке тогда и только тогда, когда при стремлении к нулю приращения аргумента 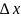приращение функции 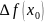тоже стремится к нулю. Следовательно, утверждение (3.2) служит определением непрерывности функции в точке, эквивалентным (3.1).

Верны следующие теоремы, описывающие свойства функций, непрерывных в некоторой точке.

Теорема 1. Сумма непрерывных функций непрерывна.

Доказательство следует из теоремы о пределе суммы. ◄

Теорема 2. Произведение непрерывных функций непрерывно.

Доказательство следует из теоремы о пределе произведения. ◄

Теорема 3. Частное непрерывных функций непрерывно в той точке, в которой знаменатель не равен нулю.

Доказательство следует из теоремы о пределе частного. ◄

Теорема 4. Сложная функция, построенная из непрерывных функций, непрерывна.

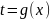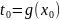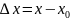Доказательство. Пусть функция непрерывна в точке , а функция непрерывна в точке , причем . Зададим приращение . Тогда получим для сложной функции приращение . В силу (3.2) 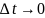при 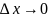и, следовательно, также . ◄

Это свойство распространяется на любое конечное число функций, участвующих в сложной функции.

Теорема 5. Обратная к монотонной непрерывной функции тоже непрерывна.

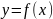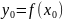Доказательство. Пусть монотонная функция , непрерывная в точке , имеет обратную функцию , причем и 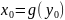. В силу взаимно-однозначной зависимости утверждения и равносильны, то есть, как из первого следует второе, так и из второго – первое, что означает непрерывность функции в точке . ◄

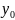Формула (2.3) и теорема о пределе постоянной доказывают, что функции и 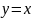непрерывны в любой точке вещественной оси. Доказано, что и остальные основные элементарные функции непрерывны в любой точке , где они определены. Тогда из свойств непрерывных функций следует очень важная

Теорема. Все элементарные функции непрерывны в любой точке своей области определения. ◄

В частности, эта теорема применяется для нахождения пределов.

Пример. Найти 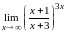(сравните решение этого примера на прошлой лекции).

Решение. Воспользуемся свойствами логарифма и возможностью перехода к пределу под знаком непрерывной функции

.◄

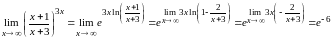Аналогично с определением односторонних пределов вводится понятие непрерывности функции справа и слева в точке . А именно, если

, (3.3)

то функция называется непрерывной слева в точке . Если

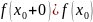, (3.4)

то функция называется непрерывной справа в точке .

Из теоремы об односторонних пределах п. 2.3. следует еще одно, эквивалентное (3.1), определение непрерывности функции в точке

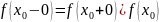. (3.5)

3.2. ФУНКЦИИ, НЕПРЕРЫВНЫЕ НА МНОЖЕСТВЕ, И ИХ СВОЙСТВА

Функция называется непрерывной в открытом интервале 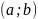, если она непрерывна в каждой точке этого интервала.

Если в граничных точках и замкнутого промежутка 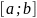функция непрерывна справа в точке и непрерывна слева в точке , то она называется непрерывной на замкнутом промежутке .

Для функций, непрерывных на замкнутом промежутке имеют место теоремы Вейерштрасса и Больцано-Коши.

Теорема Вейерштрасса.

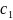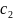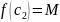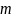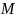Пусть функция непрерывна на . Тогда она на этом промежутке достигает наибольшего и наименьшего значений, то есть существуют точки , , принадлежащие , такие что , , где – наименьшее, а - наибольшее значения .

Теорема Больцано-Коши.

Пусть функция непрерывна на , – наименьшее, а - наибольшее значения на . Тогда для любого числа 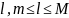, существует хотя бы одно число 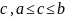, такое что .

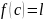3.3. КЛАССИФИКАЦИЯ РАЗРЫВОВ

Если функция не является непрерывной в точке , то есть нарушается любое определение непрерывности, то говорят, что функция имеет разрыв в точке .

Классификация разрывов строится по нарушениям определения (3.5), то есть связана с поведением функции слева и справа от точки разрыва.

Если оба односторонних предела в точке конечны, то говорят, что в этой точке разрыв первого рода. При этом различают два типа разрывов.

Устранимый разрыв. Так называется разрыв, если односторонние пределы равны одному и тому же числу, т.е.

, (3.6)

но значение функции 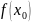не совпадает с числом или функция не определена в точке . Такую функцию можно «исправить», сделать непрерывной.

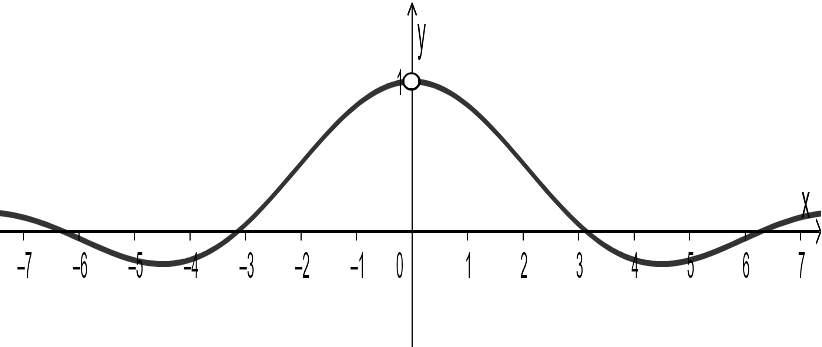
Пример. Исследовать на непрерывность функцию .

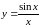Решение. Функция непрерывна на всей числовой оси кроме точки 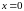(рис. 1) (теорема 3 из свойств непрерывных функций). При этом выполнено (3.6), а именно,

.

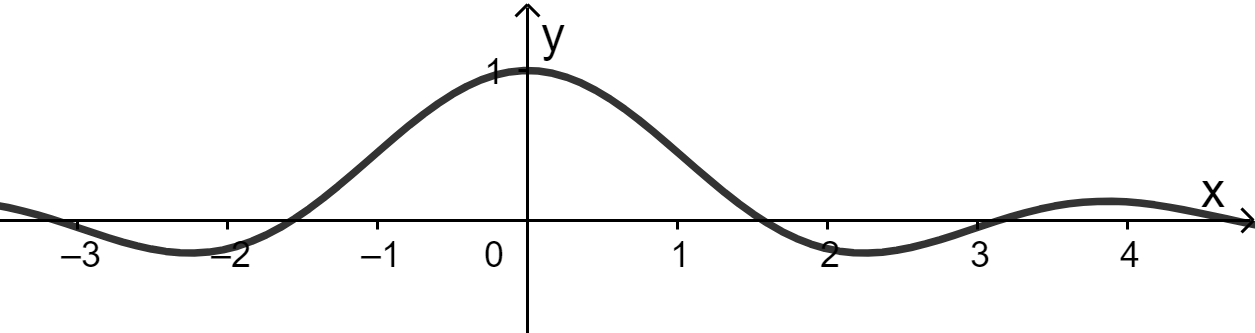
Следовательно, в точке устранимый разрыв.

Доопределив заданную функцию в точке , получаем непрерывную функцию (рис. 2).

Рис. 1

Рис. 2

Скачок. Так называется разрыв, если односторонние пределы конечны, но они не равны между собой.

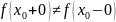. (3.7)

Величиной скачка называется разность между пределом справа и пределом слева

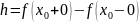. (3.8)

Пример. Исследовать на непрерывность функцию

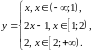
Решение. Функция непрерывна на каждом из заданных промежутков, но может терпеть разрыв на границах. Определим непрерывность в точках:

,

.

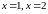
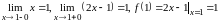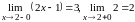Следовательно, в точке 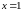функция непрерывна, а в точке имеет скачок. Величина скачка равна –1. ◄

Разрывом второго рода называется разрыв, в котором хотя бы один из односторонних пределов обращается в бесконечность или не существует.

На рисунке 3 изображены примеры функций, имеющих разрыв второго рода.

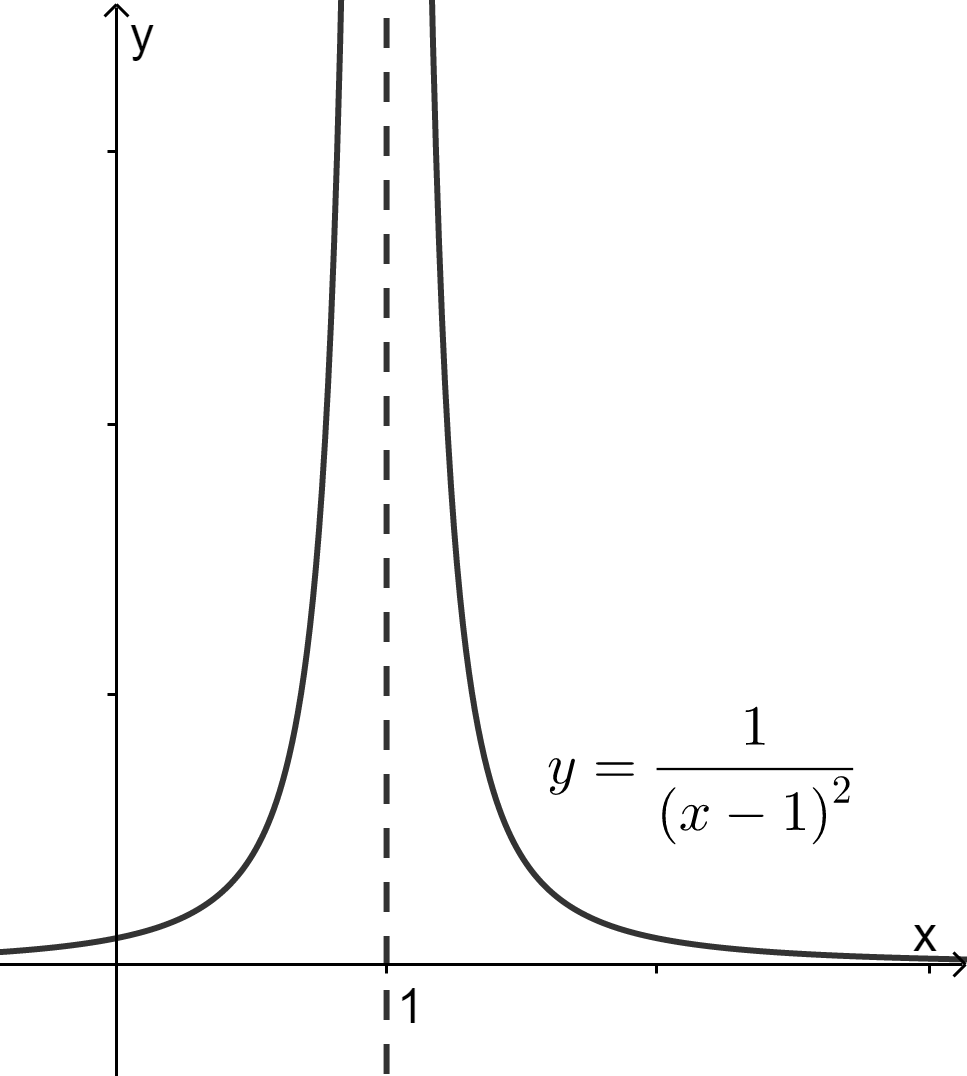
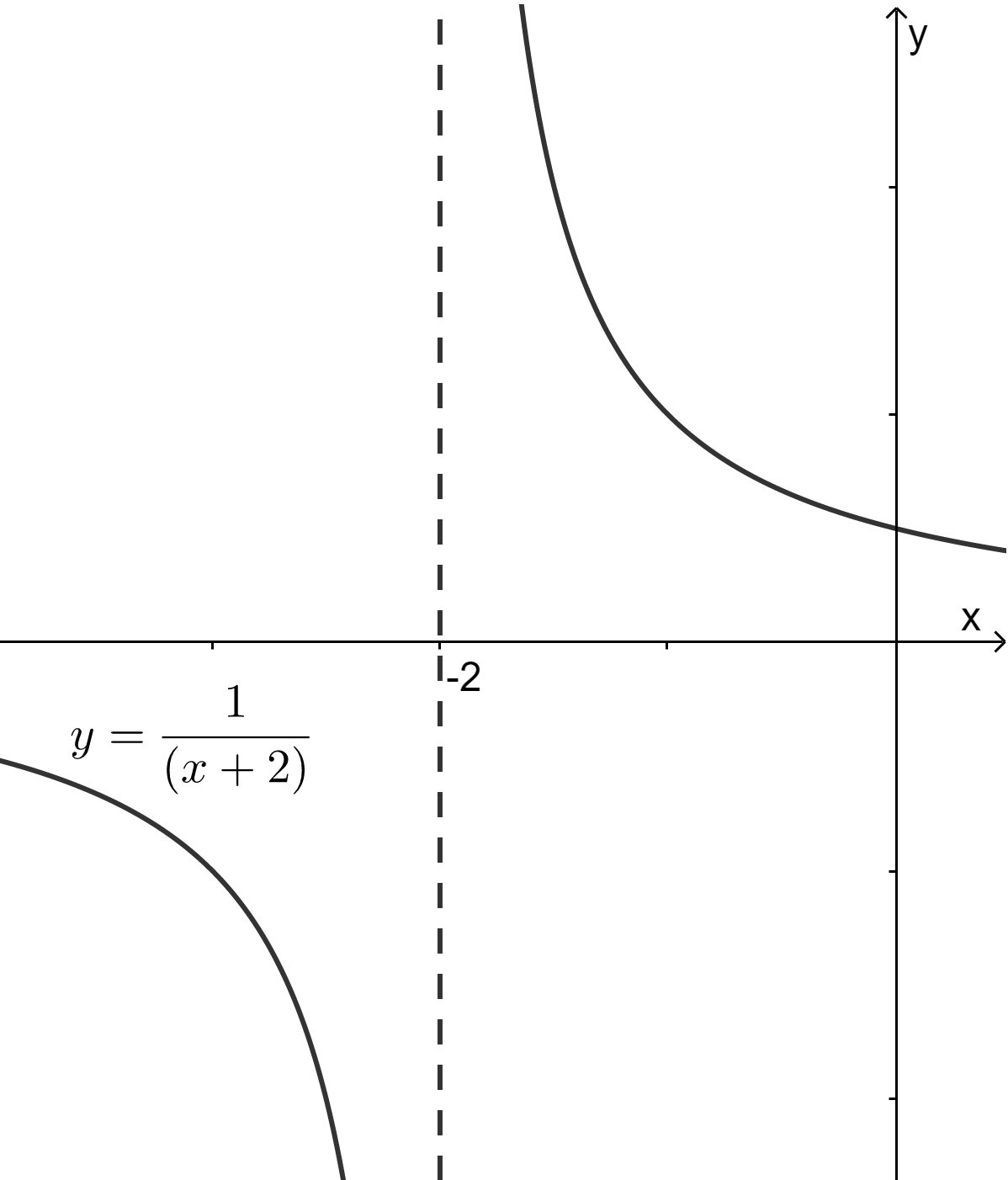
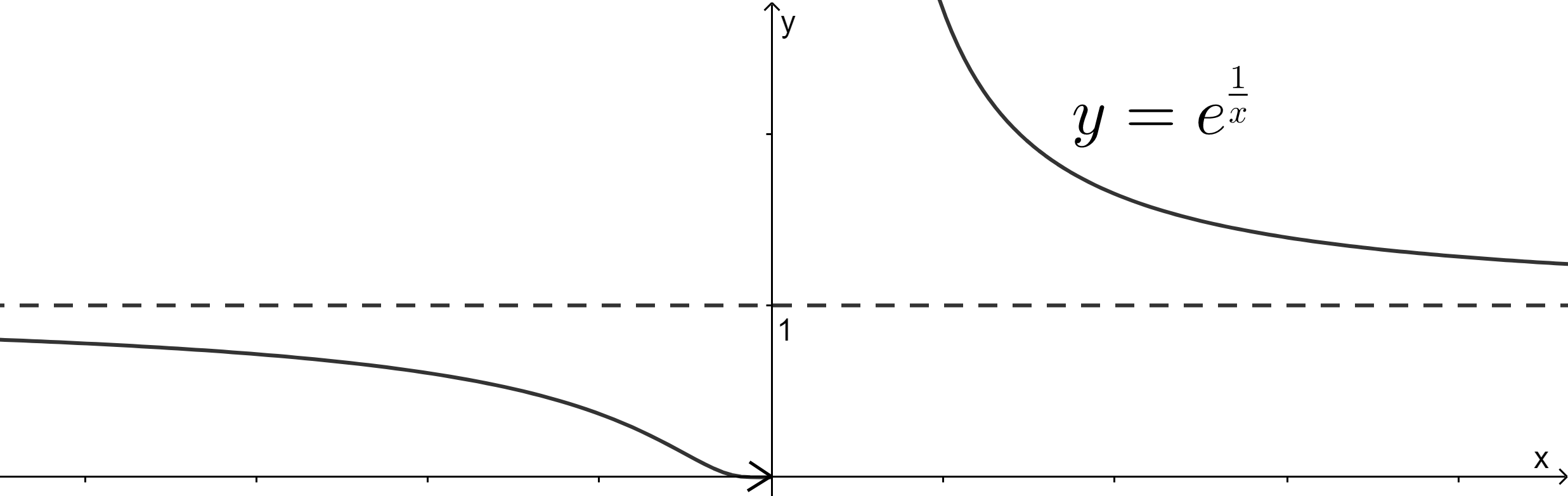
Рис. 3