2.3. Односторонние пределы
Если
переменная
стремится к числу
,
оставаясь
больше (или меньше) числа
,
и
при этом пределы функции
существуют, то такие пределы называются
односторонними
пределами.
Стремление
переменной
слева будем обозначать символом ,
стремление справа – символом
,
стремление справа – символом
 ,
а сами предельные значения функции:
,
а сами предельные значения функции:
 или
или
 соответственно.
При этом, если
соответственно.
При этом, если
 ,
обозначения упрощаются:
,
обозначения упрощаются:
 или
или
 ,
,
 или
или
 .
На бесконечности одностороннее стремление
переменной
записывается так:
.
На бесконечности одностороннее стремление
переменной
записывается так: или
,
а значения функции:
или
,
а значения функции:
 или
или
 .
.
Пример.
Найти односторонние пределы функции
 при
и
.
при
и
.
Решение.
Так как
 ,
то
,
то
 .
◄
.
◄
Связь
между пределом и
односторонними пределами показывает
следующая очевидная
Теорема.
Для существования предела функции в
некоторой точке необходимо и достаточно,
чтобы в этой точке существовали и были
равны односторонние пределы. ◄
Эта
теорема применяется, в частности, для
доказательства 1-го
замечательного предела (2.9).
Для
монотонных
функций
верна следующая
Теорема.
Пусть функция
возрастает и ограничена сверху, то есть
 ,
на промежутке
(
,
на промежутке
( - конечное число или
- конечное число или
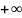 ).
Тогда существует конечный предел
).
Тогда существует конечный предел
 ,
причем
,
причем
 .
◄
.
◄
Доказательство
ее
мы здесь не приводим.
Эта
теорема применяется, в частности, для
доказательства 2-го
замечательного предела (2.10).
Следствие.
Если функция
возрастает и неограничена сверху на
промежутке
,
то
 .
.
Заметим,
что теорема верна и для неубывающей
функции
.
Аналогичное
утверждение имеет место для убывающей
и ограниченной снизу функции
.
2.4. Замечательные пределы
Так
называются следующие пределы.
1-й
замечательный предел
 .
(2.9)
.
(2.9)
Здесь
переменная
- угол в радианах. Следствия из формулы
(2.9):
 ,
,
 ,
, .
.
2-й
замечательный предел
 ,
,
 .
(2.10)
.
(2.10)
Следствия
из формулы (2.10):
 ,
,
 ,
,
 ,
,
 .
.
Часто
применяется еще один предел
 .
(2.11)
.
(2.11)
Примеры.
1)
Найти
 .
.
Решение.
Приведем к форме первого замечательного
предела (2.9)
 .
◄
.
◄
2)
Найти
 .
.
Решение.
Имеем неопределенность вида
 .
Построим выражение, похожее на второй
замечательный предел, тогда
.
Построим выражение, похожее на второй
замечательный предел, тогда
 .
◄
.
◄


 ,
стремление справа – символом
,
стремление справа – символом
 ,
а сами предельные значения функции:
,
а сами предельные значения функции:
 или
или
 соответственно.
При этом, если
соответственно.
При этом, если
 ,
обозначения упрощаются:
,
обозначения упрощаются:
 или
или
 ,
,
 или
или
 .
На бесконечности одностороннее стремление
переменной
записывается так:
.
На бесконечности одностороннее стремление
переменной
записывается так: или
,
а значения функции:
или
,
а значения функции:
 или
или
 .
. при
и
.
при
и
. ,
то
,
то .
◄
.
◄ ,
на промежутке
(
,
на промежутке
( - конечное число или
- конечное число или
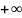 ).
Тогда существует конечный предел
).
Тогда существует конечный предел
 ,
причем
,
причем .
◄
.
◄ .
. .
(2.9)
.
(2.9) ,
,
 ,
, .
. ,
,
 .
(2.10)
.
(2.10) ,
,
 ,
, ,
,
 .
. .
(2.11)
.
(2.11) .
. .
◄
.
◄ .
. .
Построим выражение, похожее на второй
замечательный предел, тогда
.
Построим выражение, похожее на второй
замечательный предел, тогда .
◄
.
◄