Оглавление
1. ОСНОВНЫЕ ПОНЯТИЯ 1
2. ПРЕДЕЛ ФУНКЦИИ 8
2.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ 8
2.2. ТЕОРЕМЫ О ПРЕДЕЛАХ 10
2.3. ОДНОСТОРОННИЕ ПРЕДЕЛЫ 14
2.4. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ 15
1. Основные понятия
1.1.
Пусть каждому значению переменной
из множества
соответствует
одно определенное значение другой
переменной
.
Величина
называется независимой
переменной. Величина
– зависимой
переменной.
Закон, т. е. правило соответствия
между этими величинами называется
функциональной
зависимостью или
функцией
и обозначается
или
.
При этом независимая переменная
называется аргументом,
а зависимая переменная
– значением
этой функции
.
Множество
возможных значений
называется областью
определения функции
и обозначается
.
В данном пособии будем рассматривать
функции вещественного аргумента, которые
принимают вещественные значения.
Множество возможных значений
называется областью
изменения (областью значений) функции
.
Ее будем обозначать
.
Графиком
функции
называется множество точек плоскости
,
координаты которых
связаны соотношением
,
где
.
Отметим, что при таком определении мы рассматриваем однозначные функции, то есть любая вертикальная прямая пересекает график функции только в одной точке.
Функция
может быть задана различными способами:
описательно, таблично, аналитически,
графически.
Если
функция задана одной или несколькими
формулами, связывающими переменные
и
,
то
говорят, что функция
задана аналитически. Если
уравнение, связывающее переменные
и
,
разрешено
относительно переменной
,
то говорят о явно
заданной
функции.
Если связь между переменными
и
записана в виде уравнения
,
не разрешенного относительно переменной
,
то говорят, что функция задана неявно.
Зависимость
функции
от аргумента
может осуществляться через посредство
третьей переменной
,
называемой параметром.
В
этом случае говорят, что функция задана
параметрически.
В дальнейших пунктах опишем свойства функций, заданных аналитически и отражение этих свойств на графиках функций.
1.2.
Функция
называется
возрастающей
на
интервале
,
если бóльшим значениям аргумента
соответствуют бóльшие значения функции
(рис. 1,a),
т. е. для любых
,
таких что
выполняется неравенство
(1.1)
Функция называется убывающей на интервале , если бóльшим значениям аргумента соответствуют меньшие значения функции (рис. 1,б), т. е. для любых , таких что выполняется неравенство
.
(1.2)
Убывающая или возрастающая функция называется монотонной.
Функция,
сохраняющая значение на интервале
,
называется на этом интервале
постоянной
(const).
Ее график – прямая, параллельная оси
(рис. 1,в).
Если
в неравенствах (1.1)–(1.2) возможен и знак
равенства:
или
то функция
называется соответственно неубывающей
или
невозрастающей.
Рис. 1
Функция называется ограниченной на интервале , если на этом интервале выполняется неравенство
,
(1.3)
где
постоянная
.
Если на
интервале
выполняется неравенство
,
(1.4)
где
– какая-то
постоянная, то
функция
называется
ограниченной
сверху (снизу) постоянной
на
этом интервале.
1.3.
Функция
называется четной,
если область ее определения симметрична
относительно нуля и для любого значения
справедливо равенство
.
График четной функции имеет ось симметрии
– ось
.
Функция
называется нечетной,
если область ее определения симметрична
относительно нуля и для любого значения
справедливо равенство
.
График нечетной функции имеет центр
симметрии – точку
.
Примеры графиков четной и нечетной
функций представлены на рис. 2 (рис. 2,a
– четная, рис. 2,б – нечетная).
Рис. 2
1.4.
Функция
называется периодической,
если существует такое число
,
что для всех допустимых значений
справедливо
равенство
(1.5)
При
этом периодом
функции
называется
наименьшее положительное число
,
для которого верно равенство (1.5).
Примеры графиков таких функций представлены на рис. 3.
Рис. 3
1.5.
Функция называется сложной
(суперпозицией
двух функций), если ее аргумент сам
является функцией. Обозначение:
.
Область определения «внешней» (последней
по порядку действия) функции
.
должна содержать область значений
«внутренней»
.
Это определение распространяется на
любое конечное число функций.
1.6.
Пусть на множестве
задана монотонная функция
,
имеющая множество значений
.
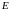Тогда между двумя переменными
и
существует взаимно-однозначное
соответствие, то есть каждому значению
одной переменной соответствует одно и
только одно значение другой. В этом
случае существует и функция
(
–
обозначение функции), которая называется
обратной
к функции
.
Графиком этих функций является одна
кривая. Если у функции
, как привычно, обозначить аргумент
буквой
,
а значение функции – буквой
,
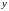то получим новую функцию
,
которую
тоже называют обратной к функции
,
что не вызывает затруднений, так как
функция (
)
– это закон соответствия.
Графики прямой
)
и такой обратной (
)
функций симметричны относительно прямой
.
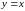Очевидно, функция
является обратной к функции
,
поэтому две функции
и
называются
взаимно-обратными.
Примеры.
1) На рисунке 4 представлены графики показательной и логарифмической функций, которые взаимно-обратны.
Рис.4
2)
Функция
не монотонная и не имеет обратной. Но
каждая из функций:
и
– монотонна в области своего задания
и имеет обратную, соответственно,
и
(см.
рис. 5).
|
|
а) |
б) |
Рис. 5
3)
Рассмотрим
функцию
.
В этом случае одному значению
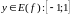соответствует бесконечное множество
значений
.
Однако на промежутке
строго убывает и принимает все значения
от 1до –1, и, значит, на нем имеет обратную
.
Обе функции изображены на рисунке 6.
Рис. 6
1.7.
Прямая, проходящая хотя бы через две
точки кривой, называется секущей.
Пусть секущая проходит через точки
и
(рис. 7,
прямая
),
причем точка
–
неподвижная точка на кривой, а точка
перемещается по кривой, приближаясь к
точке
.
Прямая, которая займет предельное
положение секущей
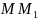называется касательной
к
кривой в точке
(рис. 7,
прямая
).
Рис. 7
Кривая, имеющая касательную, которая непрерывно меняется от точки к точке, называется гладкой.
1.8. Кривая называется выпуклой, если любая секущая пересекает ее только в двух точках.
Понятие выпуклости переносится на график функции и, тем самым, на саму функцию. Но так как график функции имеет ориентацию относительно системы координат, то для него различают следующие два случая.
Если все точки графика функции на промежутке лежат выше любой касательной, то функция называется выпуклой вниз или вогнутой на промежутке (рис. 8,a).
Если все точки графика функции на промежутке лежат ниже любой касательной, то функция называется выпуклой вверх или выпуклой на этом промежутке (рис. 8,б).
Рис. 8
Точка
называется точкой перегиба,
если в этой точке функция меняет тип
выпуклости (рис. 9)
Рис.9
1.9.
Функция имеет максимум
(минимум)
в точке
,
если существует такая окрестность этой
точки
,
принадлежащая области определения
функции, что для всех
,
выполнено неравенство
.
(1.6)
Для обозначения максимума или минимума существует объединяющий их термин – экстремум. Точка называется точкой экстремума (точкой максимума или минимума). Примеры функций, имеющих экстремум, приведены на рис. 10.
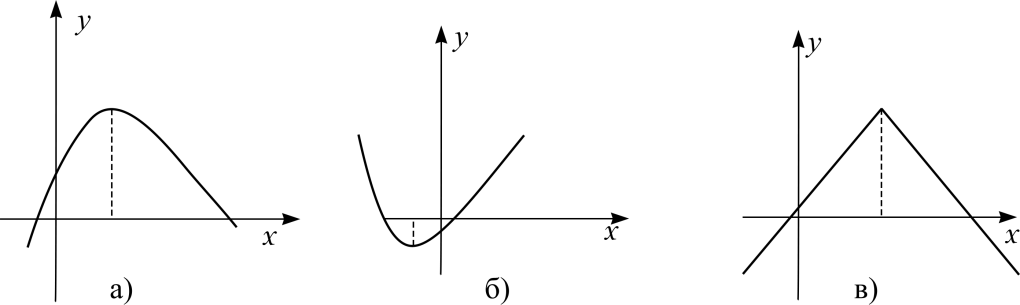
Рис. 10
1.10. Неограниченная кривая может иметь асимптоты. Асимптотой кривой называется прямая линия такая, что если двигаться по кривой, то расстояние от кривой до прямой (асимптоты) стремится к нулю.
Для
графиков различают вертикальные
и невертикальные
асимптоты,
т.к. уравнения этих прямых имеют различный
вид. Ниже приведены примеры асимптот:
вертикальная:
(рис. 11,а), наклонная:
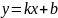(рис. 11,б), горизонтальная (частный
случай наклонной):
(рис. 11,в).
Рис. 11
1.11.
Среди множества функций, заданных
аналитически, выделяют функции, которые
называются основными
элементарными функциями:
постоянная
,
– константа; степенная
;
показательная
;
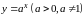логарифмическая
;
тригонометрические
;
обратные тригонометрические
,
.
Элементарными функциями называются те, которые могут быть получены из основных элементарных функций при помощи арифметических действий, сложные функции, построенные из них и обратные к ним.
Примерами элементарных функций являются:
многочлены (полиномы) –
,
где
,
при этом число
называется степенью
многочлена,
(многочлен первой степени называется
линейной
функцией,
второй степени – квадратичной);
рациональные функции (рациональные дроби):
,
где
– многочлены;
иррациональные
функции
(иррациональной
функцией называется функция, которая
задана с помощью суперпозиций рациональных
функций, степеней с рациональными
показателями и четырех арифметических
действий, например,
).
Если функция задана разными условиями на разных промежутках, то она не элементарна.
Пример.
Построить
график функции
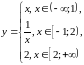
Решение. Функция строится из элементарных функций, заданных на определенных промежутках, где и построим графики этих функций. Символ «°» означает, что соответствующая точка не принадлежит графику. Окончательно получим график, изображенный на рис. 12.
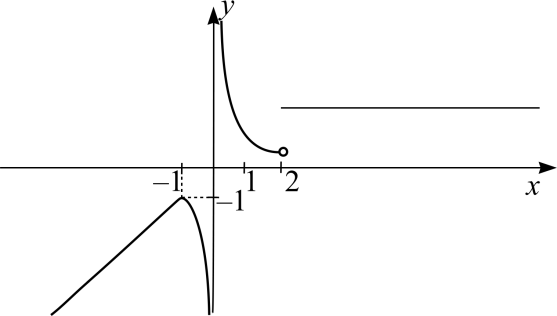
Рис. 12