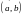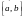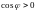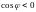Литература
1. Ефимов Н.В. Краткий курс
аналитической геометрии.— М.: Наука.,
Физматлит., 2005.— 240 с: ил.
2. Клетеник Д. В. Сборник задач
по аналитической геометрии.— М.: Наука.,
Физматлит., 1998.— 240 с: ил.
3. Данко П.Е,
Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. -
М.: Высшая школа, 2006. Ч.1.- 304 с. - Ч.1. - 416 с.
4. Гельман В.Я. Решение
математических задач средствами Excel.
– СПб. : Питер, 2003с.
Дополнительная:
5. Алексеев А.Б., Филиппова
А.Ф. Элементы линейной алгебры.
(методические указания) ––СПбГУТ.
––43с. ил.
6. Павлов Н. Excel
– готовые решения. Бери и пользуйся!
/ Николай Павлов. –М.: Книга по Требованию,
2014. –382 с. ISBN 978-5-519-01837-1.
Оглавление
Введение 3
1.
Элементы векторной алгебры в трехмерном
пространстве 4
1.1. Векторы.
Основные определения и линейные
операции 4
1.2. Скалярное
произведение векторов 10
1.3. Векторное
произведение векторов 12
1.4. Смешанное
произведение векторов 14
2.
Элементы аналитической геометрии 16
2.1. Плоскость
в пространстве 16
2.2. Прямая в
пространстве 20
2.3. Взаимное
расположение плоскостей и прямых в
пространстве 23
2.4 Кривые на
плоскости и в пространстве 35
2.5 Поверхности
второго порядка 39
Литература 45
1
Нулевой
вектор в силу произвольности его
направления считается коллинеарным,
ортогональным (см. ниже) с любым другим
вектором.
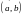
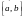

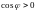

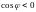
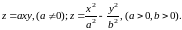
2
Для векторного и скалярного произведений
в литературе употребляются и другие
обозначения: для скалярного –
,
для векторного –
.
3
Здесь и в дальнейшем изложении под
"острым углом" между векторами
принимаем угол
,
если
,
и
,
если
, где
–
угол между векторами (рис. 2). Вычисляя
"острый угол" между векторами, в
числителе формулы (17), ставим модуль.
4
Аналогичные
поверхности (по-другому ориентированные
относительно осей координат) описывают
и уравнения: