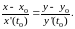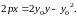2.4 Кривые на плоскости и в пространстве

Одним из удобных способов описания кривой (l) в трехмерном пространстве является задание трех уравнений вида

(36)

где каждому значению переменной t соответствует одна и только одна точка кривой (l), причем ( ) – координаты этой точки. Переменная t называется параметром, а уравнения (36) – параметрическим заданием кривой (l).

Кривая (l) называется гладкой, если функции имеют непрерывные производные и

Если на кривой задано направление, то она называется путем. В уравнениях (36) направление можно связать, например, с возрастанием параметра t.

Как известно (см., например, [1]), касательная в точке с координатами ( ) к кривой, заданной в виде (36), описывается уравнениями прямой в канонической форме

(37)

где , при этом хоть одно из чисел, стоящих в знаменателях уравнений (37), не должно равняться нулю.

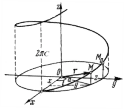
Пример 36. Найти канонические уравнения касательной к винтовой линии (рис. 19) в точке

Рис. 20	Рис. 21

Решение. На рис. 19 нарисован один виток винтовой линии, соответствующий изменения параметра t от 0 до . Точке соответствует значение .

Производные , при этом

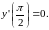
Тогда уравнения касательной

◄

Для кривой, лежащей в плоскости x0y, в уравнениях (36)

Уравнение касательной (37) в этом случае

(38)

Приведем несколько примеров таких кривых.

Окружность радиуса R с центром в точке 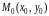(рис. 21) описывается уравнением

За параметр t удобно взять угол из полярной системы координат, если полюс совпадает с точкой , а полярная ось параллельна положительной полуоси X. Тогда уравнения (36)

Известно (см. [1]), что каноническое уравнение эллипса (рис. 22) с центром симметрии в начале координат имеет вид

			(39)
Рис. 22		Рис. 23

Следовательно, параметрическое описание эллипса имеет вид

Аналогично для гиперболы (рис. 22) (см. [1]) каноническое уравнение

(40)

В качестве параметрических уравнений (36) можно взять

где

Пример 37. Для лемнискаты Бернулли 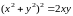написать параметрические уравнения (36) и найти касательную в точке

Решение. Используя формулы , перепишем уравнение в полярных координатах. Получим

(41)

Кривая (рис. 24) существует, если Это означает, что Возьмем за параметр t угол , т.е. . Тогда, учитывая (41), уравнения (36) примут вид:

Точке с координатами соответствует

Производные

Следовательно, уравнение касательной

Рис. 24

После преобразований окончательно получаем

◄

Если плоская кривая является графиком однозначной функции или графиком однозначной функции то в качестве параметра можно взять или соответственно.

Уравнение (38) касательной в точке с координатами в этом случае имеет вид:

или

соответственно, что приводит к стандартному уравнению

или

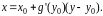
Пример 38. Для параболы (рис. 25), заданной (см. [1]) каноническим уравнением , найти касательную в точке с координатами , где

Решение. Данная парабола является графиком однозначной функции Производная 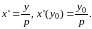Следовательно, уравнение касательной

Рис. 25

Окончательно,

◄